Уровень алгоритма

Алгоритм Тарьяна-Вишкина поиска компонент двусвязности: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
[непроверенная версия][досмотренная версия]
 
(не показано 39 промежуточных версий 3 участников)
Строка 1: Строка 1:
 +
{{algorithm
 +
| name              = Алгоритм Тарьяна-Вишкина поиска компонент двусвязности/мостов в графе
 +
| serial_complexity = <math>O(|V| + |E|)</math>
 +
| pf_height        = <math>N/A </math>
 +
| pf_width          = <math> O(|V|) </math>
 +
| input_data        = <math>O(|V| + |E|)</math>
 +
| output_data      = <math>max O(|V|)</math>
 +
}}
 +
 +
Основные авторы описания: [[Участник:Elijah|И.В.Афанасьев]]
 +
 
== Свойства и структура алгоритма ==
 
== Свойства и структура алгоритма ==
 
=== Общее описание алгоритма ===
 
=== Общее описание алгоритма ===
  
−
Параллельный '''алгоритм Тарьяна-Вишкина''' <ref>Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.</ref> находит [[Связность в графах|компоненты двухсвязности]] неориентированного графа за время <math>O(\ln n)</math> на <math>O(m + n)</math> процессорах. Алгоритм может быть адаптирован для поиска [[Связность в графах|мостов]]. Эффективность алгоритма Тарьяна-Вишкина подтверждена в последнее время<ref>Edwards, James A, and Uzi Vishkin. “Better Speedups Using Simpler Parallel Programming for Graph Connectivity and Biconnectivity,” PMAM’12, 103–114, New York, USA: ACM Press, 2012. doi:10.1145/2141702.2141714</ref><ref>Guojing Cong, and David A Bader. “An Experimental Study of Parallel Biconnected Components Algorithms on Symmetric Multiprocessors (SMPs),” 45b, IEEE, 2005. doi:10.1109/IPDPS.2005.100.</ref> как на системах архитектуры SMP, так и при вычислениях на GPU.  
+
Параллельный '''алгоритм Тарьяна-Вишкина''' <ref>Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.</ref> находит [[Связность в графах|компоненты двухсвязности]] неориентированного графа за время <math>O(\ln |V|)</math> на <math>O(|V| + |E|)</math> процессорах. Алгоритм может быть адаптирован для поиска [[Связность в графах|мостов]]. Эффективность алгоритма Тарьяна-Вишкина подтверждена в последнее время<ref>Edwards, James A, and Uzi Vishkin. “Better Speedups Using Simpler Parallel Programming for Graph Connectivity and Biconnectivity,” PMAM’12, 103–114, New York, USA: ACM Press, 2012. doi:10.1145/2141702.2141714</ref><ref>Guojing Cong, and David A Bader. “An Experimental Study of Parallel Biconnected Components Algorithms on Symmetric Multiprocessors (SMPs),” 45b, IEEE, 2005. doi:10.1109/IPDPS.2005.100.</ref> как на системах архитектуры SMP, так и при вычислениях на GPU.
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
−
В задаче поиска компонент сильной связности требуется разбить вершины ориентированного графа на непересекающиеся группы (компоненты), так что в каждой компоненты все вершины достижимы друг из друга по рёбрам графа (с учётом направления).
 
  
−
Пусть задан ориентированный граф <math>G=(V,E)</math> с вершинами <math>V= (v_1,v_2,...,v_n)</math> и рёбрами <math>E=(e_1,e_2,...,e_m)</math>.  
+
1. Для каждой компоненты связности графа найти какое-либо остовное дерево <math>T</math>.
 +
 
 +
2. Перенумеровать вершины <math>T</math> в порядке обратного обхода  <math>N(v) </math>.
 +
 
 +
3. В порядке возрастания номера вершины <math>N(v) </math> выполнить следующие действия:
 +
 
 +
a. <math>D(v) := 1+ \sum_{v \rightarrow w}D(w) </math>, величины <math>D(W)</math> определяются рекурсивно, <math>D(W)=1</math> для концевых вершин.
  
−
Путём между вершинами <math>u</math> и <math>v</math> называется последовательность рёбер <math>\pi_{uv}=(e_1,...,e_k)</math>, начинающаяся в вершине <math>u</math> и заканчивающаяся в вершине <math>v</math>, так что началом каждого следующего ребра служит конец предыдущего.
+
b. <math> L(v) := \min { \{N(v) - D(v)+1 \} \cup \{ L(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }</math>
  
−
Если существует такой путь <math>\pi_{uv}</math>, то вершина <math>v</math> достижима из вершины <math>u</math>. Считается, что от вершины <math>u</math> к самой себе ведёт пустой путь <math>\pi_{uu}</math>, то есть каждая вершина достижима из самой себя. Непустой путь <math>\pi_{uu}</math> называется циклом (замкнутым обходом).
+
c. <math> H(v) := \max { \{ N(v) \} \cup \{ H(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }</math>
  
−
Ориентированный граф называется сильно связным, если всякая его вершина <math>v</math> достижима из любой другой его вершины <math>u</math>. Компонентой сильной связности ориентированного графа называется любой максимальный по включению сильно связный подграф.
+
d. Пометить ребро <math>v \rightarrow w</math> мостом, если <math>H(w)<=N(w)</math> и <math>L(w) > N(w)-D(w)</math>.
  
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
 +
 +
Наиболее вычислительно затратной частью алгоритма является поиск в ширину в исходном графе, вычисляющий величины <math>N(v)</math>. В свою очередь, вычислительным ядром данного поиска в ширину является  обход вершин, смежных к выбранной вершине <math>v</math>, с последующем добавлением еще не посещенных вершин в стек.
 +
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
 +
 +
На первом шаге работы алгоритма строится остовный лес графа с использованием модифицированного алгоритма Шилоаха-Вишкина.
 +
 +
Для этого для каждой вершины <math>v</math> определяется указатель на родительскую вершину <math>P(v)</math>; на шаге инициализации <math>P(v):=v</math>. Далее остовный лес строится чередованием двух параллельных операций:
 +
 +
• Удвоение указателей: <math>P(v):=P(P(v))</math> ;
 +
 +
• Соединение: <math>P(P(v)):=P(w)</math>, где <math>v</math> – вершина <math>P</math>-дерева ( <math>P(v)=v</math>на текущем шаге),  <math>w</math>– некоторая вершина, для которой существует ребро <math>(v,w)\in E</math>. Ребро помечается, как принадлежащее остовному лесу .
 +
 +
Далее производятся следующие шаги:
 +
 +
• перенумерация вершин в обратном порядке обхода (post-order);
 +
 +
• вычисление количества потомков <math>D(v)</math> для каждой вершины;
 +
 +
• вычисление значений <math>L(v)</math> и <math>H(v)</math> для каждой вершины;
 +
 +
• пометка рёбер <math>v \rightarrow w</math> мостами, если <math>H(w)<=N(w)</math> и <math>L(w) > N(w)-D(w)</math>.
 +
 +
Основной идеей для обеспечения завершения работы алгоритма за <math>O( \ln |V|)</math> шагов является систематическое использование операции удвоения указателей.
  
 
=== Схема реализации последовательного алгоритма ===
 
=== Схема реализации последовательного алгоритма ===
 +
 +
На первом шаге работы алгоритма строится остовный лес графа при помощи последовательных вызовов поисков в ширину от еще не посещенных на предыдущих шагах вершин. При необходимости может быть выполнен шаг Trim, выделяющий вершины, принадлежащие связанным компонентам единичного размера.
 +
 +
После этого производится построение остовного дерева при помощи поиска в глубину, с подсчетом величин <math>D(v)</math>.
 +
 +
Затем производятся вычисления величин <math>L</math> и <math>H</math> по формулам, приведенным в пунктах b,c в предыдущем разделе.
 +
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
  
−
Последовательный вариант алгоритма аналогичен [[Алгоритм Тарьяна поиска компонент двусвязности|алгоритму Тарьяна]]<ref>Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.</ref> и имеет линейную сложность <math>O(m + n)</math>.
+
Последовательный вариант алгоритма аналогичен [[Алгоритм Тарьяна поиска компонент двусвязности|алгоритму Тарьяна]]<ref>Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.</ref> и имеет линейную сложность <math>O(|E| + |V|)</math>.
  
 
=== Информационный граф ===
 
=== Информационный граф ===
 +
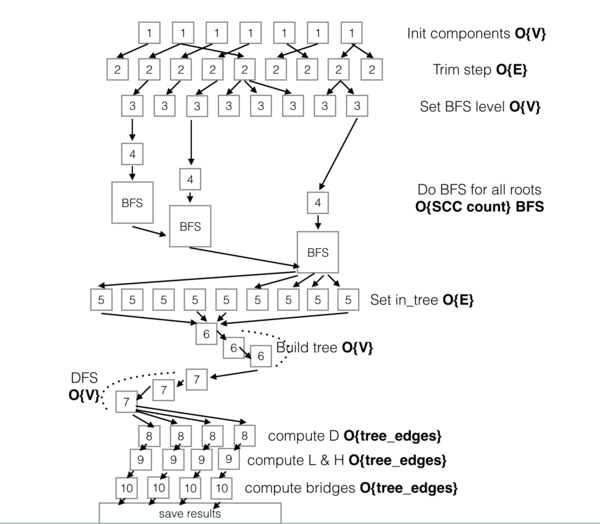
Далее на рисунке 1 представлен информационный граф алгоритма, демонстрирующий его основные уровни параллелизма.
 +
 +
[[file:tarjan_vishkin_ig.png|thumb|center|600px|Рисунок 1 – Информационный граф алгоритма Тарьяна-Вышкина]]
 +
 +
В начале работы алгоритм производит инциализацию связанных компонент графа [1], с последующим выделением тривиальных компонент (размера 1 и 2) [2]; затем, производится инициализация уровней для всех вершин [3] при помощи последовательных поисков в ширину [4],[BFS], выполняемых до тех пор, пока все вершины не будут размечены различными уровнями.
 +
 +
Далее производится поиск ребер, вошедших в остовное дерево [5], с последовательным построением данного дерева на основе поиска в глубину [6],[7]. После этого друг за другом производится вычисление необходимых метрик для каждой из вершин L, H и D [8],[9]. Перед завершением работы алгоритма на основе данных метрик производится вычисление мостов в графе [10].
 +
 
=== Ресурс параллелизма алгоритма ===
 
=== Ресурс параллелизма алгоритма ===
  
−
Алгоритм изначально параллельный, время работы <math>O(\ln n)</math> на <math>O(m + n)</math> процессорах.
+
Алгоритм изначально разрабатывался для параллельной реализации, его время работы составляет <math>O(\ln(|V|))</math> на <math>O(|V| + |E|)</math> процессорах.
 +
 
 +
Изначальные инициализации связанных компонент и уровней вершин [1] и [3] могут выполняться параллельно за <math>O(|V|)</math> операций. Шаг трим [2] так же может быть выполнен за <math>O(|E|)</math> параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем [[Поиск_в_ширину_(BFS)|разделе]].
 +
 
 +
Нумерация вершин <math>D(v)</math> в обратном порядке обходе графа производится при помощи поиска в глубину [5],[6], который должен выполняться сугубо последовательно за <math>O(|V|)</math> операций, и может, вообще говоря, серьезно снизить производительность реализации на параллельных архитектурах.
 +
 
 +
Каждое из вычислений величин <math>L</math>, <math>H</math>, а так же проверка ребер на свойство, является ли каждое их них мостом [8],[9],[10], может выполняться параллельно за <math>O(|V|)</math> операций.
 +
 
 +
Таким образом, ширина ярусно-параллельной формы алгоритма равна <math>O(|E|)</math>, а высота ЯПФ, вообще говоря, зависит от структуры входного графа (числа связанных компонент, и, как следствие, числа необходимых поисков в ширину).
  
 
=== Входные и выходные данные алгоритма ===
 
=== Входные и выходные данные алгоритма ===
 +
 +
'''Входные данные''': граф <math>G(V, E)</math>, <math>|V|</math> вершин <math>v_i</math> и <math>|E|</math> рёбер <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math>.
 +
 +
'''Объём входных данных''': <math>O(|V| + |E|)</math>.
 +
 +
'''Выходные данные'''
 +
 +
Список ребер, являющихся мостами в графе.
 +
 +
'''Объём выходных данных''':
 +
 +
1. <math>O(|E|)</math> в случае хранения массива принадлежности каждого ребра к множеству мостов в графе
 +
 +
2. <math>max O(|V|)</math> в случае хранения мостов в виде списка пар вершин
 +
 
=== Свойства алгоритма ===
 
=== Свойства алгоритма ===
 
1. Компонента сильной связности – подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.
 
1. Компонента сильной связности – подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.
Строка 36: Строка 113:
 
== Программная реализация алгоритма ==
 
== Программная реализация алгоритма ==
 
=== Особенности реализации последовательного алгоритма ===
 
=== Особенности реализации последовательного алгоритма ===
−
=== Локальность данных и вычислений ===
 
−
==== Локальность реализации алгоритма ====
 
−
===== Структура обращений в память и качественная оценка локальности =====
 
−
===== Количественная оценка локальности =====
 
 
=== Возможные способы и особенности параллельной реализации алгоритма ===
 
=== Возможные способы и особенности параллельной реализации алгоритма ===
−
=== Масштабируемость алгоритма и его реализации ===
+
 
−
==== Масштабируемость алгоритма ====
+
Программа, реализующая алгоритм Тарьяна-Вышкина, состоит из двух частей: CPU части, отвечающей за параллельные вычисления на многоядерных CPU, а так же копирование данных на GPU и общее управлениями вычислениями, и GPU части, отвечающей только за вычисления на  графическом ускорителе.
−
==== Масштабируемость реализации алгоритма ====
+
 
−
=== Динамические характеристики и эффективность реализации алгоритма ===
+
=== Результаты прогонов ===
 
=== Выводы для классов архитектур ===
 
=== Выводы для классов архитектур ===
−
=== Существующие реализации алгоритма ===
 
  
 
== Литература ==
 
== Литература ==
 +
 
<references />
 
<references />
  
−
[[Категория:Начатые статьи]]
+
[[Категория:Статьи в работе]]
 +
 
 +
[[En:Tarjan-Vishkin biconnected components algorithm]]

Текущая версия на 15:50, 6 июля 2022


Алгоритм Тарьяна-Вишкина поиска компонент двусвязности/мостов в графе
Последовательный алгоритм
Последовательная сложность [math]O(|V| + |E|)[/math]
Объём входных данных [math]O(|V| + |E|)[/math]
Объём выходных данных [math]max O(|V|)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]N/A [/math]
Ширина ярусно-параллельной формы [math] O(|V|) [/math]


Основные авторы описания: И.В.Афанасьев

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Параллельный алгоритм Тарьяна-Вишкина [1] находит компоненты двухсвязности неориентированного графа за время [math]O(\ln |V|)[/math] на [math]O(|V| + |E|)[/math] процессорах. Алгоритм может быть адаптирован для поиска мостов. Эффективность алгоритма Тарьяна-Вишкина подтверждена в последнее время[2][3] как на системах архитектуры SMP, так и при вычислениях на GPU.

1.2 Математическое описание алгоритма

1. Для каждой компоненты связности графа найти какое-либо остовное дерево [math]T[/math].

2. Перенумеровать вершины [math]T[/math] в порядке обратного обхода [math]N(v) [/math].

3. В порядке возрастания номера вершины [math]N(v) [/math] выполнить следующие действия:

a. [math]D(v) := 1+ \sum_{v \rightarrow w}D(w) [/math], величины [math]D(W)[/math] определяются рекурсивно, [math]D(W)=1[/math] для концевых вершин.

b. [math] L(v) := \min { \{N(v) - D(v)+1 \} \cup \{ L(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]

c. [math] H(v) := \max { \{ N(v) \} \cup \{ H(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]

d. Пометить ребро [math]v \rightarrow w[/math] мостом, если [math]H(w)\lt =N(w)[/math] и [math]L(w) \gt N(w)-D(w)[/math].

1.3 Вычислительное ядро алгоритма

Наиболее вычислительно затратной частью алгоритма является поиск в ширину в исходном графе, вычисляющий величины [math]N(v)[/math]. В свою очередь, вычислительным ядром данного поиска в ширину является обход вершин, смежных к выбранной вершине [math]v[/math], с последующем добавлением еще не посещенных вершин в стек.

1.4 Макроструктура алгоритма

На первом шаге работы алгоритма строится остовный лес графа с использованием модифицированного алгоритма Шилоаха-Вишкина.

Для этого для каждой вершины [math]v[/math] определяется указатель на родительскую вершину [math]P(v)[/math]; на шаге инициализации [math]P(v):=v[/math]. Далее остовный лес строится чередованием двух параллельных операций:

• Удвоение указателей: [math]P(v):=P(P(v))[/math] ;

• Соединение: [math]P(P(v)):=P(w)[/math], где [math]v[/math] – вершина [math]P[/math]-дерева ( [math]P(v)=v[/math]на текущем шаге), [math]w[/math]– некоторая вершина, для которой существует ребро [math](v,w)\in E[/math]. Ребро помечается, как принадлежащее остовному лесу .

Далее производятся следующие шаги:

• перенумерация вершин в обратном порядке обхода (post-order);

• вычисление количества потомков [math]D(v)[/math] для каждой вершины;

• вычисление значений [math]L(v)[/math] и [math]H(v)[/math] для каждой вершины;

• пометка рёбер [math]v \rightarrow w[/math] мостами, если [math]H(w)\lt =N(w)[/math] и [math]L(w) \gt N(w)-D(w)[/math].

Основной идеей для обеспечения завершения работы алгоритма за [math]O( \ln |V|)[/math] шагов является систематическое использование операции удвоения указателей.

1.5 Схема реализации последовательного алгоритма

На первом шаге работы алгоритма строится остовный лес графа при помощи последовательных вызовов поисков в ширину от еще не посещенных на предыдущих шагах вершин. При необходимости может быть выполнен шаг Trim, выделяющий вершины, принадлежащие связанным компонентам единичного размера.

После этого производится построение остовного дерева при помощи поиска в глубину, с подсчетом величин [math]D(v)[/math].

Затем производятся вычисления величин [math]L[/math] и [math]H[/math] по формулам, приведенным в пунктах b,c в предыдущем разделе.

1.6 Последовательная сложность алгоритма

Последовательный вариант алгоритма аналогичен алгоритму Тарьяна[4] и имеет линейную сложность [math]O(|E| + |V|)[/math].

1.7 Информационный граф

Далее на рисунке 1 представлен информационный граф алгоритма, демонстрирующий его основные уровни параллелизма.

Рисунок 1 – Информационный граф алгоритма Тарьяна-Вышкина

В начале работы алгоритм производит инциализацию связанных компонент графа [1], с последующим выделением тривиальных компонент (размера 1 и 2) [2]; затем, производится инициализация уровней для всех вершин [3] при помощи последовательных поисков в ширину [4],[BFS], выполняемых до тех пор, пока все вершины не будут размечены различными уровнями.

Далее производится поиск ребер, вошедших в остовное дерево [5], с последовательным построением данного дерева на основе поиска в глубину [6],[7]. После этого друг за другом производится вычисление необходимых метрик для каждой из вершин L, H и D [8],[9]. Перед завершением работы алгоритма на основе данных метрик производится вычисление мостов в графе [10].

1.8 Ресурс параллелизма алгоритма

Алгоритм изначально разрабатывался для параллельной реализации, его время работы составляет [math]O(\ln(|V|))[/math] на [math]O(|V| + |E|)[/math] процессорах.

Изначальные инициализации связанных компонент и уровней вершин [1] и [3] могут выполняться параллельно за [math]O(|V|)[/math] операций. Шаг трим [2] так же может быть выполнен за [math]O(|E|)[/math] параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем разделе.

Нумерация вершин [math]D(v)[/math] в обратном порядке обходе графа производится при помощи поиска в глубину [5],[6], который должен выполняться сугубо последовательно за [math]O(|V|)[/math] операций, и может, вообще говоря, серьезно снизить производительность реализации на параллельных архитектурах.

Каждое из вычислений величин [math]L[/math], [math]H[/math], а так же проверка ребер на свойство, является ли каждое их них мостом [8],[9],[10], может выполняться параллельно за [math]O(|V|)[/math] операций.

Таким образом, ширина ярусно-параллельной формы алгоритма равна [math]O(|E|)[/math], а высота ЯПФ, вообще говоря, зависит от структуры входного графа (числа связанных компонент, и, как следствие, числа необходимых поисков в ширину).

1.9 Входные и выходные данные алгоритма

Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].

Объём входных данных: [math]O(|V| + |E|)[/math].

Выходные данные

Список ребер, являющихся мостами в графе.

Объём выходных данных:

1. [math]O(|E|)[/math] в случае хранения массива принадлежности каждого ребра к множеству мостов в графе

2. [math]max O(|V|)[/math] в случае хранения мостов в виде списка пар вершин

1.10 Свойства алгоритма

1. Компонента сильной связности – подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.

2. Компонента сильной связности является объединением всех циклом, проходящих через её вершины.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Возможные способы и особенности параллельной реализации алгоритма

Программа, реализующая алгоритм Тарьяна-Вышкина, состоит из двух частей: CPU части, отвечающей за параллельные вычисления на многоядерных CPU, а так же копирование данных на GPU и общее управлениями вычислениями, и GPU части, отвечающей только за вычисления на графическом ускорителе.

2.3 Результаты прогонов

2.4 Выводы для классов архитектур

3 Литература

  1. ↑ Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.
  2. ↑ Edwards, James A, and Uzi Vishkin. “Better Speedups Using Simpler Parallel Programming for Graph Connectivity and Biconnectivity,” PMAM’12, 103–114, New York, USA: ACM Press, 2012. doi:10.1145/2141702.2141714
  3. ↑ Guojing Cong, and David A Bader. “An Experimental Study of Parallel Biconnected Components Algorithms on Symmetric Multiprocessors (SMPs),” 45b, IEEE, 2005. doi:10.1109/IPDPS.2005.100.
  4. ↑ Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.
Источник — https://algowiki-project.org/w/ru/index.php?title=Алгоритм_Тарьяна-Вишкина_поиска_компонент_двусвязности&oldid=28999