Алгоритм распространения констант для задачи поиска сообществ в социальном графе: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
LanaLana (обсуждение | вклад) |
LanaLana (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
Автор студенческой работы: [[Участник:LanaLana|Светлана Илларионова]] | Автор студенческой работы: [[Участник:LanaLana|Светлана Илларионова]] | ||
| − | == | + | = Свойства и структура алгоритмов = |
| − | |||
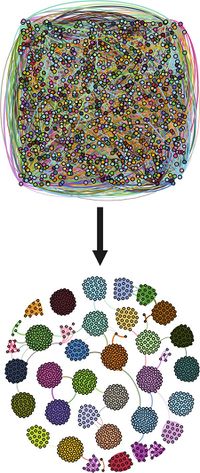
[[file: Search-communities.jpg|thumb|right|200px|Рисунок 1. Пример разбиения на сообщества]] | [[file: Search-communities.jpg|thumb|right|200px|Рисунок 1. Пример разбиения на сообщества]] | ||
| + | == Общее описание алгоритма== | ||
| + | Рассматривается задача поиска сообществ в неориенетированном графе с весами, значениями которых являются действительными неотрицательными числами. | ||
| + | В качестве подхода к решению будем рассматривать алгоритм Label Propagation. | ||
| + | Вершины одного сообщества должны быть сильно связаны, а вершины из разных сообществ должны быть слабо связаны. | ||
| − | + | == Математическое описание алгоритма == | |
Дан граф <math> G = (V, E)</math>, где <math> V </math> — множество вершин, <math> E </math> — множество ребер, <math> w (u, v) </math> — вес каждого ребра <math> e(u, v) \in E, u, v \in V</math>. | Дан граф <math> G = (V, E)</math>, где <math> V </math> — множество вершин, <math> E </math> — множество ребер, <math> w (u, v) </math> — вес каждого ребра <math> e(u, v) \in E, u, v \in V</math>. | ||
| Строка 26: | Строка 29: | ||
<math>m</math> — нормализующий коэффициент, сумма весов рёбер графа. | <math>m</math> — нормализующий коэффициент, сумма весов рёбер графа. | ||
| − | |||
| + | == Вычислительное ядро алгоритма == | ||
| + | == Макроструктура алгоритма== | ||
| + | == Схема реализации последовательного алгоритма== | ||
| + | В начальный момент времени каждой вершине приписана уникальная метка сообщества. Обновление меток вершин осуществляется по следующему принципу: у каждой вершины есть определенное число смежных вершин, которым приписаны метки каких-то сообществ, также у ребер между вершинами определены свои веса. На очередном шаге определим метку вершины <math>current</math>. У соседей этой вершины метки сообществ, к которым они принадлежат, могут быть различными. Рассмотрим каждый тип меток. Для вершин <math>i</math>-го типа считаем сумму весов ребер, которые соединяют эти вершины с изучаемой вершиной <math>current</math>. Приписываем нашей вершине ту метку, для которой эта сумма оказалась максимальной. Итерации происходят до тех пор, пока меняются метки вершин. В стандартном алгоритме принято рассматривать вершины в случайном порядке, это позволяет улучшить метрику. Можно отказаться от переупорядочивания вершин для увеличения быстродействия вычислений. Также в параллельной версии программы потоки в рамках одного узла могут конкурировать, производить вычисления неравномерно, засчёт чего достигается эффект случайности в обработке вершин. | ||
| + | == Последовательная сложность алгоритма== | ||
| + | == Информационный граф== | ||
| + | == Ресурс параллелизма алгоритма== | ||
| + | Разбиваем множество вершин на заданное число узлов. Каждый узел пересчитывает метки для своего набора вершин. Массивы меток для всех вершин синхронизируются с помощью операции MPI_Allgather. | ||
| − | + | == Входные и выходные данные алгоритма== | |
| − | |||
| − | == | ||
| − | + | На вход алгоритму подаётся граф, который хранится как разреженная матрица смежности в формате CSR. | |
| + | Тестирование производилось на графах LFR (Lancichinetti-Fortunato-Radicchi), которые широко используются для анализа работы методов выделения сообществ в графах, так как являются хорошо приближенными к реальным моделям. | ||
| + | == Свойства алгоритма== | ||
| + | К достоинствам алгоритма Label Propagation можно отнести следующие его аспекты: | ||
* время работы | * время работы | ||
* количество итераций слабо зависит от размера графа | * количество итераций слабо зависит от размера графа | ||
| Строка 43: | Строка 54: | ||
* при некоторых входных данных может давать плохие решения | * при некоторых входных данных может давать плохие решения | ||
| − | + | =Программная реализация алгоритма= | |
| + | ==Особенности реализации последовательного алгоритма== | ||
| + | ==Локальность данных и вычислений== | ||
| + | ==Возможные способы и особенности параллельной реализации алгоритма== | ||
| + | ==Масштабируемость алгоритма и его реализации== | ||
| + | ==Динамические характеристики и эффективность реализации алгоритма== | ||
| + | ==Выводы для классов архитектур== | ||
| + | ==Существующие реализации алгоритма== | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Алгоритм решения== | ||
| + | |||
| + | |||
| − | + | ||
| + | |||
| − | + | ||
== Результаты работы алгоритма == | == Результаты работы алгоритма == | ||
Версия 16:29, 20 ноября 2016
Автор студенческой работы: Светлана Илларионова
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 2.8 Алгоритм решения
- 2.9 Результаты работы алгоритма
- 2.10 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Рассматривается задача поиска сообществ в неориенетированном графе с весами, значениями которых являются действительными неотрицательными числами. В качестве подхода к решению будем рассматривать алгоритм Label Propagation. Вершины одного сообщества должны быть сильно связаны, а вершины из разных сообществ должны быть слабо связаны.
1.2 Математическое описание алгоритма
Дан граф [math] G = (V, E)[/math], где [math] V [/math] — множество вершин, [math] E [/math] — множество ребер, [math] w (u, v) [/math] — вес каждого ребра [math] e(u, v) \in E, u, v \in V[/math].
Цель задачи — найти такое разбиение графа [math]G[/math] на множество [math]C[/math] непересекающихся сообществ вершин [math]c_i \subseteq V[/math]: [math] \cup c_i = V, \forall c_i \in C [/math] [math] c_i \cap c_j = \varnothing, \forall c_i, c_j \in C, i \neq j, [/math] чтобы максимизировать функционал модулярности [math]Q[/math]:
[math] Q = \sum_{c \in C} \left(\frac{\sum_{in}^{c}}{m} - \left[\frac{\sum{out}^{c}}{m} \right]^2\right)[/math],
где [math] \sum_{in}^{c} = \sum_{u, v \in c, e(u, v) \in E} w(u, v), [/math]
[math] \sum_{out}^{c} = \sum_{in}^{c} + \sum_{u \in c, v \notin c, e(u, v) \in E} w(u, v)[/math],
[math] m = \sum_{e(u, v) \in E} w(u, v).[/math]
[math]\sum_{in}^{c} [/math] — сумма весов всех внутренних рёбер сообщества.
[math]\sum_{out}^{c} [/math] — сумма весов всех рёбер, исходящих из вершин сообщества.
[math]m[/math] — нормализующий коэффициент, сумма весов рёбер графа.
1.3 Вычислительное ядро алгоритма
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
В начальный момент времени каждой вершине приписана уникальная метка сообщества. Обновление меток вершин осуществляется по следующему принципу: у каждой вершины есть определенное число смежных вершин, которым приписаны метки каких-то сообществ, также у ребер между вершинами определены свои веса. На очередном шаге определим метку вершины [math]current[/math]. У соседей этой вершины метки сообществ, к которым они принадлежат, могут быть различными. Рассмотрим каждый тип меток. Для вершин [math]i[/math]-го типа считаем сумму весов ребер, которые соединяют эти вершины с изучаемой вершиной [math]current[/math]. Приписываем нашей вершине ту метку, для которой эта сумма оказалась максимальной. Итерации происходят до тех пор, пока меняются метки вершин. В стандартном алгоритме принято рассматривать вершины в случайном порядке, это позволяет улучшить метрику. Можно отказаться от переупорядочивания вершин для увеличения быстродействия вычислений. Также в параллельной версии программы потоки в рамках одного узла могут конкурировать, производить вычисления неравномерно, засчёт чего достигается эффект случайности в обработке вершин.
1.6 Последовательная сложность алгоритма
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Разбиваем множество вершин на заданное число узлов. Каждый узел пересчитывает метки для своего набора вершин. Массивы меток для всех вершин синхронизируются с помощью операции MPI_Allgather.
1.9 Входные и выходные данные алгоритма
На вход алгоритму подаётся граф, который хранится как разреженная матрица смежности в формате CSR. Тестирование производилось на графах LFR (Lancichinetti-Fortunato-Radicchi), которые широко используются для анализа работы методов выделения сообществ в графах, так как являются хорошо приближенными к реальным моделям.
1.10 Свойства алгоритма
К достоинствам алгоритма Label Propagation можно отнести следующие его аспекты:
- время работы
- количество итераций слабо зависит от размера графа
- прост в понимании
Недостатками алгоритма являются:
- недетерминированность, то есть на одном и том же наборе входных данных при новом запуске результат может получиться отличным от предыдущего
- при некоторых входных данных может давать плохие решения
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
2.8 Алгоритм решения
2.9 Результаты работы алгоритма
Тестирование производилось на графах LFR (Lancichinetti-Fortunato-Radicchi), которые широко используются для анализа работы методов выделения сообществ в графах, так как являются хорошо приближенными к реальным моделям.
Размер графа [math]2^{18}[/math], средняя степень вершины 200. Без OpenMP.
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 1 | 29.7823 s. |
| 2 | 1 | 15.4772 s. |
| 4 | 1 | 8.2046 s. |
| 8 | 1 | 5.09298 s. |
Размер графа [math]2^{18}[/math], средняя степень вершины 200. С OpenMP.
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 4 | 9.21499 s. |
| 2 | 4 | 4.37143 s. |
| 4 | 4 | 3.41528 s. |
| 8 | 4 | 3.87224 s. |
Размер графа [math]2^{21}[/math], средняя степень вершин 30. Без OpenMP
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 1 | 68.7771 s. |
| 2 | 1 | 36.1929 s |
| 4 | 1 | 21.6286 s. |
| 8 | 1 | 23.8237 s. |
Размер графа [math]2^{21}[/math], средняя степень вершин 30. C OpenMP
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 4 | 21.5797 s. |
| 2 | 4 | 11.7228 s. |
| 4 | 4 | 11.5657 s. |
Алгоритм перестает масштабироваться, начиная с определенного момента, когда время синхронизации меток для вершин становится соразмерным с временем вычисления меток. Чем менье степень вершин, тем раньше алгоритм перестает масштабироваться.
2.10 Литература
1. "Lancichinetti-Fortunato-Radicchi Benchmark." Wikipedia, the free encyclopedia. 30 October 2015. Web. 13 November 2016 https://en.wikipedia.org/wiki/Lancichinetti-Fortunato-Radicchi_Benchmark
2. "Help:Wiki markup." Wikipedia, the free encyclopedia. 12 November 2016. Web. 13 November 2016 https://en.wikipedia.org/wiki/Help:Wiki_markup
3. "Label Propagation Algorithm." 9 November 2016. Web. 13 November 2016. https://en.wikipedia.org/wiki/Label_Propagation_Algorithm
4. Спецкурс "Параллельная обработка больших графов" Лекция 4. к.т.н. Александр Сергеевич Семенов. 11 November 2016. Web. 13 November 2016. http://dislab.org/PLGP/PLGP_lecture4.pdf
5. "Sparse matrix." Wikipedia, the free encyclopedia. 30 October 2016. Web. 13 November 2016. https://en.wikipedia.org/wiki/Sparse_matrix
6. А.С.Антонов "Параллельное программирование с использованием технологии MPI".-М.: Изд-во МГУ, 2004.-71 с.
7. "OpenMP 4.5 Specifications" Nov 2015. Web. http://www.openmp.org/wp-content/uploads/openmp-4.5.pdf