Алгоритм распространения констант для задачи поиска сообществ в социальном графе: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
LanaLana (обсуждение | вклад) |
LanaLana (обсуждение | вклад) |
||
| Строка 37: | Строка 37: | ||
== Последовательная сложность алгоритма== | == Последовательная сложность алгоритма== | ||
| + | Сложность алгоритма: <math>O(n + m)</math>, где <math>n, m</math> — число вершин и ребер. | ||
| + | |||
== Информационный граф== | == Информационный граф== | ||
== Ресурс параллелизма алгоритма== | == Ресурс параллелизма алгоритма== | ||
Версия 21:05, 20 ноября 2016
Автор студенческой работы: Светлана Илларионова
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
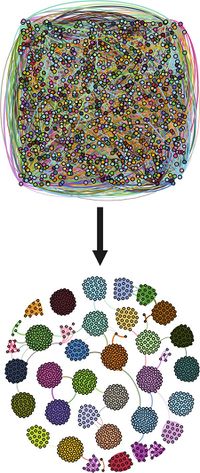
Рассматривается задача поиска сообществ в неориенетированном графе с весами, значениями которых являются действительными неотрицательными числами. Приведем примеры, где в реальной жизни могут втсречаться такие структуры: задачи, возникающие в социальной медиа структуре (то есть это многочисленные социальные сети), задачи, связанные с медициной и биоинформатикой, бизнес-задачи. Главная идея, которую преследуют, решая вышеперечисленные проблемы — это выделение из общей совокупности объектов, групп, объекты внутри которых сильно взаимосвязаны. В качестве подхода к решению будем рассматривать алгоритм Label Propagation, применяя который получим, что вершины одного сообщества будут сильно связаны, а вершины из разных сообществ будут слабо связаны.
1.2 Математическое описание алгоритма
Дан граф [math] G = (V, E)[/math], где [math] V [/math] — множество вершин, [math] E [/math] — множество ребер, [math] w (u, v) [/math] — вес каждого ребра [math] e(u, v) \in E, u, v \in V[/math].
Цель задачи — найти такое разбиение графа [math]G[/math] на множество [math]C[/math] непересекающихся сообществ вершин [math]c_i \subseteq V[/math]: [math] \cup c_i = V, \forall c_i \in C [/math] [math] c_i \cap c_j = \varnothing, \forall c_i, c_j \in C, i \neq j, [/math] чтобы максимизировать функционал модулярности [math]Q[/math]:
[math] Q = \sum_{c \in C} \left(\frac{\sum_{in}^{c}}{m} - \left[\frac{\sum{out}^{c}}{m} \right]^2\right)[/math],
где [math] \sum_{in}^{c} = \sum_{u, v \in c, e(u, v) \in E} w(u, v), [/math]
[math] \sum_{out}^{c} = \sum_{in}^{c} + \sum_{u \in c, v \notin c, e(u, v) \in E} w(u, v)[/math],
[math] m = \sum_{e(u, v) \in E} w(u, v).[/math]
[math]\sum_{in}^{c} [/math] — сумма весов всех внутренних рёбер сообщества.
[math]\sum_{out}^{c} [/math] — сумма весов всех рёбер, исходящих из вершин сообщества.
[math]m[/math] — нормализующий коэффициент, сумма весов рёбер графа.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро — та часть алгоритма, на которую приходится основное время работы алгоритма. В данном случае к вычислительному ядру не относится только часть инициализации. Вычислительное ядро включает в себя цикл, в котором необходимое число раз осуществляется прохождение по всем вершинам графа и отнесения их к соответствующим компонентам.
1.4 Макроструктура алгоритма
???
1.5 Схема реализации последовательного алгоритма
В начальный момент времени каждой вершине приписана уникальная метка сообщества. Обновление меток вершин осуществляется по следующему принципу: у каждой вершины есть определенное число смежных вершин, которым приписаны метки каких-то сообществ, также у ребер между вершинами определены свои веса. На очередном шаге определим метку вершины [math]current[/math]. У соседей этой вершины метки сообществ, к которым они принадлежат, могут быть различными. Рассмотрим каждый тип меток. Для вершин [math]i[/math]-го типа считаем сумму весов ребер, которые соединяют эти вершины с изучаемой вершиной [math]current[/math]. Приписываем нашей вершине ту метку, для которой эта сумма оказалась максимальной. Итерации происходят до тех пор, пока меняются метки вершин. В стандартном алгоритме принято рассматривать вершины в случайном порядке, это позволяет улучшить метрику. Можно отказаться от переупорядочивания вершин для увеличения быстродействия вычислений. Также в параллельной версии программы потоки в рамках одного узла могут конкурировать, производить вычисления неравномерно, засчёт чего достигается эффект случайности в обработке вершин.
1.6 Последовательная сложность алгоритма
Сложность алгоритма: [math]O(n + m)[/math], где [math]n, m[/math] — число вершин и ребер.
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Разбиваем множество вершин на заданное число узлов. Каждый узел пересчитывает метки для своего набора вершин. Массивы меток для всех вершин синхронизируются с помощью операции MPI_Allgather.
1.9 Входные и выходные данные алгоритма
На вход алгоритму подаётся граф, который хранится как разреженная матрица смежности в формате CSR. Тестирование производилось на графах LFR (Lancichinetti-Fortunato-Radicchi), которые широко используются для анализа работы методов выделения сообществ в графах, так как являются хорошо приближенными к реальным моделям.
1.10 Свойства алгоритма
К достоинствам алгоритма Label Propagation можно отнести следующие его аспекты:
- время работы
- количество итераций слабо зависит от размера графа
- прост в понимании
Недостатками алгоритма являются:
- недетерминированность, то есть на одном и том же наборе входных данных при новом запуске результат может получиться отличным от предыдущего
- при некоторых входных данных может давать плохие решения
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Тестирование производилось на графах LFR (Lancichinetti-Fortunato-Radicchi), которые широко используются для анализа работы методов выделения сообществ в графах, так как являются хорошо приближенными к реальным моделям.
Размер графа [math]2^{18}[/math], средняя степень вершины 200. Без OpenMP.
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 1 | 29.7823 s. |
| 2 | 1 | 15.4772 s. |
| 4 | 1 | 8.2046 s. |
| 8 | 1 | 5.09298 s. |
Размер графа [math]2^{18}[/math], средняя степень вершины 200. С OpenMP.
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 4 | 9.21499 s. |
| 2 | 4 | 4.37143 s. |
| 4 | 4 | 3.41528 s. |
| 8 | 4 | 3.87224 s. |
Размер графа [math]2^{21}[/math], средняя степень вершин 30. Без OpenMP
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 1 | 68.7771 s. |
| 2 | 1 | 36.1929 s |
| 4 | 1 | 21.6286 s. |
| 8 | 1 | 23.8237 s. |
Размер графа [math]2^{21}[/math], средняя степень вершин 30. C OpenMP
| Число процессов | Число потоков | Время (с) |
|---|---|---|
| 1 | 4 | 21.5797 s. |
| 2 | 4 | 11.7228 s. |
| 4 | 4 | 11.5657 s. |
Алгоритм перестает масштабироваться, начиная с определенного момента, когда время синхронизации меток для вершин становится соразмерным с временем вычисления меток. Чем менье степень вершин, тем раньше алгоритм перестает масштабироваться.
3 Литература
1. "Lancichinetti-Fortunato-Radicchi Benchmark." Wikipedia, the free encyclopedia. 30 October 2015. Web. 13 November 2016 https://en.wikipedia.org/wiki/Lancichinetti-Fortunato-Radicchi_Benchmark
2. "Help:Wiki markup." Wikipedia, the free encyclopedia. 12 November 2016. Web. 13 November 2016 https://en.wikipedia.org/wiki/Help:Wiki_markup
3. "Label Propagation Algorithm." 9 November 2016. Web. 13 November 2016. https://en.wikipedia.org/wiki/Label_Propagation_Algorithm
4. Спецкурс "Параллельная обработка больших графов" Лекция 4. к.т.н. Александр Сергеевич Семенов. 11 November 2016. Web. 13 November 2016. http://dislab.org/PLGP/PLGP_lecture4.pdf
5. "Sparse matrix." Wikipedia, the free encyclopedia. 30 October 2016. Web. 13 November 2016. https://en.wikipedia.org/wiki/Sparse_matrix
6. А.С.Антонов "Параллельное программирование с использованием технологии MPI".-М.: Изд-во МГУ, 2004.-71 с.
7. "OpenMP 4.5 Specifications" Nov 2015. Web. http://www.openmp.org/wp-content/uploads/openmp-4.5.pdf