Блочная прогонка: различия между версиями
| [досмотренная версия] | [досмотренная версия] |
Frolov (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| (не показаны 23 промежуточные версии 2 участников) | |||
| Строка 1: | Строка 1: | ||
{{algorithm | {{algorithm | ||
| − | | name = Прогонка для блочно-трёхдиагональной матрицы | + | | name = Прогонка для блочно-трёхдиагональной матрицы<br /> |
| serial_complexity = <math>8n-7</math> макроопераций | | serial_complexity = <math>8n-7</math> макроопераций | ||
| pf_height = <math>3n-2</math> макроопераций | | pf_height = <math>3n-2</math> макроопераций | ||
| pf_width = <math>2</math> макроопераций | | pf_width = <math>2</math> макроопераций | ||
| − | | input_data = <math>4n-2</math> | + | | input_data = <math>4n-2</math> блоков |
| − | | output_data = <math>n</math> | + | | output_data = <math>n</math> блоков |
}} | }} | ||
| Строка 15: | Строка 15: | ||
'''Блочная прогонка''' - один из вариантов метода исключения неизвестных в приложении к решению блочно-трёхдиагональной СЛАУ<ref name="VOLA">Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref name="MIV">Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref> вида <math>Ax = b</math>, где | '''Блочная прогонка''' - один из вариантов метода исключения неизвестных в приложении к решению блочно-трёхдиагональной СЛАУ<ref name="VOLA">Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref name="MIV">Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref> вида <math>Ax = b</math>, где | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {{Шаблон:Блочно-трёхдиагональная СЛАУ}} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
или, если записывать отдельно по блочным уравнениям, то | или, если записывать отдельно по блочным уравнениям, то | ||
| − | + | ||
| − | + | <math>C_{0} Y_{0} - B_{0} Y_{1} = F_{0}</math>, | |
| − | -A_{i} Y_{i-1} + C_{i} Y_{i} - B_{i} Y_{i+1} = F_{i}, 1 \le i \le N-1, | + | |
| − | -A_{N} Y_{N-1} + C_{N} Y_{N} = F_{N} | + | <math>-A_{i} Y_{i-1} + C_{i} Y_{i} - B_{i} Y_{i+1} = F_{i}</math>, <math>1 \le i \le N-1</math>, |
| − | </math> | + | |
| + | <math>-A_{N} Y_{N-1} + C_{N} Y_{N} = F_{N}</math> | ||
Суть метода - в исключении из уравнений неизвестных, сначала - сверху вниз - под диагональю, а потом - снизу вверх - над диагональю. | Суть метода - в исключении из уравнений неизвестных, сначала - сверху вниз - под диагональю, а потом - снизу вверх - над диагональю. | ||
| Строка 73: | Строка 34: | ||
В приведённых обозначениях в прогонке сначала выполняют её прямой ход - вычисляют матричные коэффициенты | В приведённых обозначениях в прогонке сначала выполняют её прямой ход - вычисляют матричные коэффициенты | ||
| − | + | <math>\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}</math>, | |
| − | \boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}, | + | |
| − | \boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0}, | + | <math>\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0}</math>, |
| − | \boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}, \quad i = 1, 2, \cdots , N-1, | + | |
| − | \boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i}), \quad i = 1, 2, \cdots , N | + | <math>\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}</math>, где <math>\quad i = 1, 2, \cdots , N-1</math>, |
| − | </math> | + | |
| + | <math>\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i})</math>, где <math>\quad i = 1, 2, \cdots , N</math>. | ||
| + | |||
после чего вычисляют решение с помощью обратного хода | после чего вычисляют решение с помощью обратного хода | ||
| − | + | ||
| − | Y_{N} = \boldsymbol{\beta}_{N+1}, | + | <math>Y_{N} = \boldsymbol{\beta}_{N+1}</math>, |
| − | Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}, \quad i = N-1, N-2, \cdots , 1, 0 | + | |
| − | </math> | + | <math>Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}</math>, где <math>\quad i = N-1, N-2, \cdots , 1, 0</math>. |
Данные формулы эквиваленты вычислению одного из блочных <math>LU</math>-разложений матрицы системы с последующим решением блочно-двухдиагональных систем методом обратной подстановки. | Данные формулы эквиваленты вычислению одного из блочных <math>LU</math>-разложений матрицы системы с последующим решением блочно-двухдиагональных систем методом обратной подстановки. | ||
| + | |||
| + | В случае малоразмерных (порядка 2 или 3) блоков вполне возможна ситуация, когда обращение в формулах <math>(C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}</math> выполняется явно, и соответствующие блоки вычисляются и хранятся. | ||
| + | |||
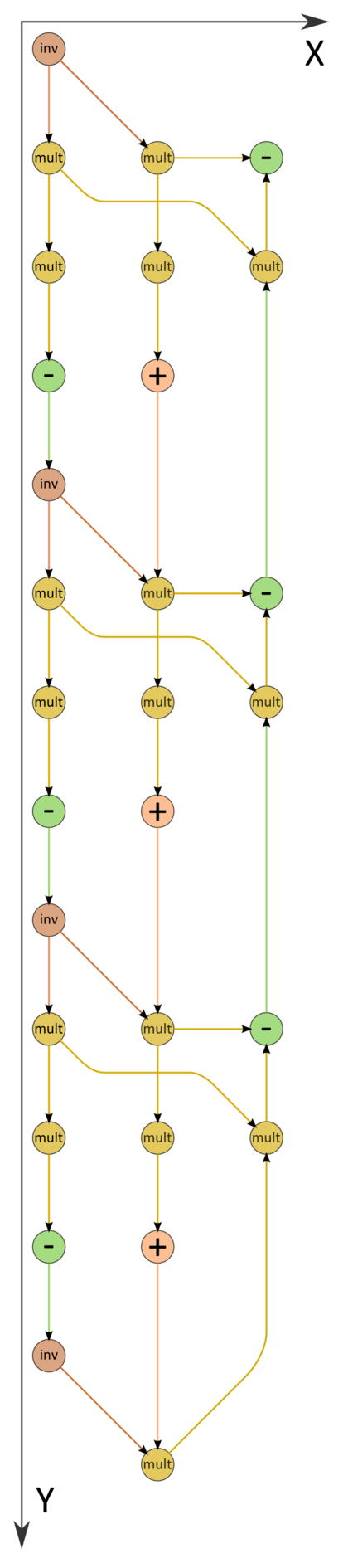
| + | [[file:ProgonkaInv.png|thumb|left|420px|Рисунок 2. Детальный граф алгоритма блочной прогонки с однократным вычислением обратных блоков при n=4 без отображения входных и выходных данных. '''inv''' - вычисление обратного блока, '''mult''' - операция перемножения блоков. Серым цветом выделены операции, повторяющиеся при замене правой части СЛАУ]] | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| Строка 101: | Строка 68: | ||
1. Инициализируется прямой ход прогонки: | 1. Инициализируется прямой ход прогонки: | ||
| − | + | <math>\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}</math>, | |
| − | \boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}, | + | |
| − | \boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0} | + | <math>\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0}</math>. |
| − | </math> | ||
2. Последовательно для всех i от 1 до N-1 выполняются формулы прямого хода: | 2. Последовательно для всех i от 1 до N-1 выполняются формулы прямого хода: | ||
| − | + | <math>\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}</math>, | |
| − | \boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}, | + | |
| − | \boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i}) | + | <math>\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i})</math> |
| − | </math> | ||
3. Инициализируется обратный ход прогонки: | 3. Инициализируется обратный ход прогонки: | ||
| − | + | <math>Y_{N} = (C_{N}-A_{N}\boldsymbol{\alpha}_{N})^{-1}(F_{N}+A_{N}\boldsymbol{\beta}_{N})</math> | |
| − | Y_{N} = (C_{N}-A_{N}\boldsymbol{\alpha}_{N})^{-1}(F_{N}+A_{N}\boldsymbol{\beta}_{N}) | ||
| − | </math> | ||
4. Последовательно для всех i с убыванием от N-1 до 0 выполняются формулы обратного хода: | 4. Последовательно для всех i с убыванием от N-1 до 0 выполняются формулы обратного хода: | ||
| − | + | <math>Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}.</math> | |
| − | Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}. | ||
| − | </math> | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| Строка 128: | Строка 89: | ||
Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется: | Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется: | ||
| − | * <math>2n-1</math> | + | * <math>2n-1</math> умножений обратного одному блока на другой, |
| − | * <math>3n-3</math> сложений/вычитаний, | + | * <math>3n-3</math> сложений/вычитаний блоков, |
| − | * <math>3n-3</math> умножений. | + | * <math>3n-3</math> умножений блоков. |
| − | При классификации по последовательной сложности, таким образом, прогонка относится к алгоритмам ''с линейной сложностью''. | + | При классификации по последовательной сложности, таким образом, блочная прогонка относится к алгоритмам ''с линейной блочной сложностью''. |
=== Информационный граф === | === Информационный граф === | ||
| − | Информационный | + | Информационный '''макро'''граф прогонки изображён на рис.1. Как видно, в терминах макроопераций он почти последователен: при выполнении прямого хода две ветви (левая - блочное разложение матрицы, центральная - решение первой из блочно-двухдиагональных систем) могут выполняться параллельно друг другу. Правая ветвь соответствует обратному ходу. По рисунку видно, что не только математическая суть обработки подвекторов, но даже структура макрографа алгоритма и направление потоков данных в нём вполне соответствуют названию "обратный ход". |
| + | На рис.2 изображена версия блочной прогонки, в которой благодаря малоразмерности блоков сразу можно вычислить обратный блок. | ||
=== Описание ресурса параллелизма алгоритма === | === Описание ресурса параллелизма алгоритма === | ||
| Строка 149: | Строка 111: | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| − | '''Входные данные''': блочно-трёхдиагональная матрица <math>A</math> (блоки <math> | + | '''Входные данные''': блочно-трёхдиагональная матрица <math>A</math> (блоки <math>A_{ij}</math>), вектор <math>B</math> (блоки <math>B_{i}</math>). |
'''Выходные данные''': вектор <math>X</math> (блоки <math>X_i</math> ). | '''Выходные данные''': вектор <math>X</math> (блоки <math>X_i</math> ). | ||
| Строка 170: | Строка 132: | ||
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| − | В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже | + | В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже блоков матрицы либо отдельно). |
| − | |||
=== Возможные способы и особенности параллельной реализации алгоритма === | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| − | + | ||
| − | === | + | По макрографу алгоритма видно, что он почти последователен. В связи с этим самый очевидный из способов распараллеливания - распараллеливание блочных операций, из которых составлен алгоритм. Естественно, что оно зависит от размера блоков и их возможной разрежённости. |
| + | |||
| + | === Результаты прогонов === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | + | ||
| + | Учитывая последовательность макрографа и то, что эффективно распараллеливать можно только блочные операции, видно, что для данного алгоритма не подходит реализация на архитектурах типа кластерной и т.п. с распределёнными ресурсами, а более эффективной была бы реализация на ускорителях типа графических плат. | ||
| + | При малых размерах блоков, однако, и она не будет давать достаточный эффект. | ||
== Литература == | == Литература == | ||
| Строка 184: | Строка 149: | ||
[[Категория:Статьи в работе]][[Категория:Блочные алгоритмы]] | [[Категория:Статьи в работе]][[Категория:Блочные алгоритмы]] | ||
| + | |||
| + | [[en:Block Thomas algorithm]] | ||
Текущая версия на 09:44, 18 июля 2022
| Прогонка для блочно-трёхдиагональной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]8n-7[/math] макроопераций |
| Объём входных данных | [math]4n-2[/math] блоков |
| Объём выходных данных | [math]n[/math] блоков |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]3n-2[/math] макроопераций |
| Ширина ярусно-параллельной формы | [math]2[/math] макроопераций |
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Блочная прогонка - один из вариантов метода исключения неизвестных в приложении к решению блочно-трёхдиагональной СЛАУ[1][2] вида [math]Ax = b[/math], где
- [math] A = \begin{bmatrix} A_{11} & A_{12} & 0 & \cdots & \cdots & 0 \\ A_{21} & A_{22} & A_{23}& \cdots & \cdots & 0 \\ 0 & A_{32} & A_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & A_{n-1 n-2} & A_{n-1 n-1} & A_{n-1 n} \\ 0 & \cdots & \cdots & 0 & A_{n n-1} & A_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \\ \end{bmatrix}, b = \begin{bmatrix} B_{1} \\ B_{2} \\ \vdots \\ B_{n} \\ \end{bmatrix} [/math]
Часто, однако, при изложении сути метода блочной прогонки[3] блоки правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид ([math]N=n+1[/math])
- [math] A = \begin{bmatrix} C_{0} & -B_{0} & 0 & \cdots & \cdots & 0 \\ -A_{1} & C_{1} & -B_{1} & \cdots & \cdots & 0 \\ 0 & -A_{2} & C_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -A_{N-1} & C_{N-1} & -B_{N-1} \\ 0 & \cdots & \cdots & 0 & -A_{N} & C_{N} \\ \end{bmatrix}\begin{bmatrix} Y_{0} \\ Y_{1} \\ \vdots \\ Y_{N} \\ \end{bmatrix} = \begin{bmatrix} F_{0} \\ F_{1} \\ \vdots \\ F_{N} \\ \end{bmatrix} [/math]
или, если записывать отдельно по блочным уравнениям, то
[math]C_{0} Y_{0} - B_{0} Y_{1} = F_{0}[/math],
[math]-A_{i} Y_{i-1} + C_{i} Y_{i} - B_{i} Y_{i+1} = F_{i}[/math], [math]1 \le i \le N-1[/math],
[math]-A_{N} Y_{N-1} + C_{N} Y_{N} = F_{N}[/math]
Суть метода - в исключении из уравнений неизвестных, сначала - сверху вниз - под диагональю, а потом - снизу вверх - над диагональю.
1.2 Математическое описание алгоритма
В приведённых обозначениях в прогонке сначала выполняют её прямой ход - вычисляют матричные коэффициенты
[math]\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}[/math],
[math]\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0}[/math],
[math]\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}[/math], где [math]\quad i = 1, 2, \cdots , N-1[/math],
[math]\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i})[/math], где [math]\quad i = 1, 2, \cdots , N[/math].
после чего вычисляют решение с помощью обратного хода
[math]Y_{N} = \boldsymbol{\beta}_{N+1}[/math],
[math]Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}[/math], где [math]\quad i = N-1, N-2, \cdots , 1, 0[/math].
Данные формулы эквиваленты вычислению одного из блочных [math]LU[/math]-разложений матрицы системы с последующим решением блочно-двухдиагональных систем методом обратной подстановки.
В случае малоразмерных (порядка 2 или 3) блоков вполне возможна ситуация, когда обращение в формулах [math](C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}[/math] выполняется явно, и соответствующие блоки вычисляются и хранятся.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно представить из двух частей - прямого и обратного хода. В прямом ходе ядро составляют последовательности операций умножения обратной к одной матрице на другую, умножения и сложения/вычитания матриц и векторов. В обратном ходе в ядре остаются только последовательности умножения и сложения матриц и векторов.
1.4 Макроструктура алгоритма
Кроме представления макроструктуры алгоритма как совокупности прямого и обратного хода, прямой ход также может быть разложен на две макроединицы - разложения матрицы и прямого хода решения двухдиагональной СЛАУ, которые выполняются "одновременно", т.е., параллельно друг другу. При этом решение двухдиагональной СЛАУ использует результаты разложения.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Инициализируется прямой ход прогонки:
[math]\boldsymbol{\alpha}_{1} = C_{0}^{-1} B_{0}[/math],
[math]\boldsymbol{\beta}_{1} = C_{0}^{-1} F_{0}[/math].
2. Последовательно для всех i от 1 до N-1 выполняются формулы прямого хода:
[math]\boldsymbol{\alpha}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1} B_{i}[/math],
[math]\boldsymbol{\beta}_{i+1} = (C_{i}-A_{i}\boldsymbol{\alpha}_{i})^{-1}(F_{i}+A_{i}\boldsymbol{\beta}_{i})[/math]
3. Инициализируется обратный ход прогонки:
[math]Y_{N} = (C_{N}-A_{N}\boldsymbol{\alpha}_{N})^{-1}(F_{N}+A_{N}\boldsymbol{\beta}_{N})[/math]
4. Последовательно для всех i с убыванием от N-1 до 0 выполняются формулы обратного хода: [math]Y_{i} = \boldsymbol{\alpha}_{i+1} Y_{i+1} + \boldsymbol{\beta}_{i+1}.[/math]
1.6 Последовательная сложность алгоритма
Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется:
- [math]2n-1[/math] умножений обратного одному блока на другой,
- [math]3n-3[/math] сложений/вычитаний блоков,
- [math]3n-3[/math] умножений блоков.
При классификации по последовательной сложности, таким образом, блочная прогонка относится к алгоритмам с линейной блочной сложностью.
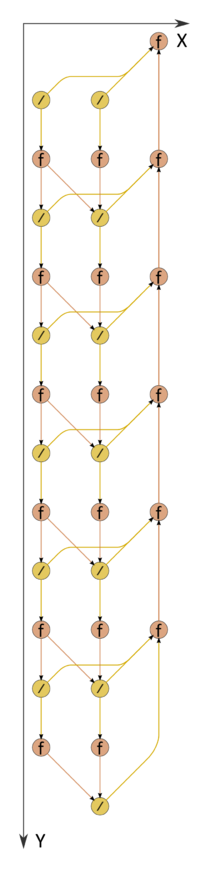
1.7 Информационный граф
Информационный макрограф прогонки изображён на рис.1. Как видно, в терминах макроопераций он почти последователен: при выполнении прямого хода две ветви (левая - блочное разложение матрицы, центральная - решение первой из блочно-двухдиагональных систем) могут выполняться параллельно друг другу. Правая ветвь соответствует обратному ходу. По рисунку видно, что не только математическая суть обработки подвекторов, но даже структура макрографа алгоритма и направление потоков данных в нём вполне соответствуют названию "обратный ход". На рис.2 изображена версия блочной прогонки, в которой благодаря малоразмерности блоков сразу можно вычислить обратный блок.
1.8 Описание ресурса параллелизма алгоритма
Для выполнения прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в параллельном варианте требуется последовательно выполнить следующие макроярусы:
- [math]n[/math] ярусов умножения матрицы, обратной к одной, на другую или на вектор (в каждом из ярусов, кроме одного, по 2 деления),
- по [math]2n - 2[/math] ярусов умножений и сложений/вычитаний мариц и векторов (в n-1 ярусах - по 2 операции, в n-1 - по одной).
При классификации по высоте ЯПФ, таким образом, прогонка относится к алгоритмам с макросложностью [math]O(n)[/math]. При классификации по ширине ЯПФ его макросложность будет [math]2[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: блочно-трёхдиагональная матрица [math]A[/math] (блоки [math]A_{ij}[/math]), вектор [math]B[/math] (блоки [math]B_{i}[/math]).
Выходные данные: вектор [math]X[/math] (блоки [math]X_i[/math] ).
Объём выходных данных: [math]n[/math] блоков.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной макросложности, как хорошо видно, является константой (причём менее 2).
При этом вычислительная мощность алгоритма, как отношение числа макроопераций к суммарному объему входных и выходных макроданных – тоже константа.
Алгоритм полностью детерминирован, если фиксированы все размеры блоков и способы выполнения операций над ними. Последние, однако, могут широко варьироваться на практике.
Обычно прогонка используется для решения СЛАУ с диагональным преобладанием. Тогда гарантируется устойчивость алгоритма. В случае, когда требуется решение нескольких СЛАУ с одной и той же матрицей, левую ветвь вычислений (см. рисунок с графом алгоритма) можно не повторять. Это связано с тем, что блочное [math]LU[/math]-разложение матрицы системы не нужно перевычислять.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже блоков матрицы либо отдельно).
2.2 Возможные способы и особенности параллельной реализации алгоритма
По макрографу алгоритма видно, что он почти последователен. В связи с этим самый очевидный из способов распараллеливания - распараллеливание блочных операций, из которых составлен алгоритм. Естественно, что оно зависит от размера блоков и их возможной разрежённости.
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
Учитывая последовательность макрографа и то, что эффективно распараллеливать можно только блочные операции, видно, что для данного алгоритма не подходит реализация на архитектурах типа кластерной и т.п. с распределёнными ресурсами, а более эффективной была бы реализация на ускорителях типа графических плат. При малых размерах блоков, однако, и она не будет давать достаточный эффект.