Метод Хаусхолдера (отражений) QR-разложения квадратной матрицы, вещественный точечный вариант: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Frolov (обсуждение | вклад) |
Frolov (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | '''Метод Хаусхолдера''' (в советской математической литературе называется также '''методом отражений''') используется для разложения матриц в виде <math>A=QR</math> (<math>Q</math> - унитарная, <math>R</math> — правая треугольная матрица)<ref>В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.</ref>,<ref name="VOLA">Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref> | + | '''Метод Хаусхолдера''' (в советской математической литературе называется также '''методом отражений''') используется для разложения матриц в виде <math>A=QR</math> (<math>Q</math> - унитарная, <math>R</math> — правая треугольная матрица)<ref>В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.</ref>. При этом матрица <math>Q</math> хранится и используется не в своём явном виде, а в виде произведения матриц отражения<ref name="VOLA">Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref>. Каждая из матриц отражения может быть определена одним вектором. Это позволяет в классическом исполнении метода отражений хранить результаты разложения на месте матрицы A с использованием минимального одномерного дополнительного массива. |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 15: | Строка 15: | ||
На <math>i</math>-м шаге метода с помощью преобразования отражения "убираются" ненулевые поддиагональные элементы в <math>i</math>-м столбце. Таким образом, после <math>n-1</math> шагов преобразований получается матрица <math>R</math> из <math>QR</math>-разложения. | На <math>i</math>-м шаге метода с помощью преобразования отражения "убираются" ненулевые поддиагональные элементы в <math>i</math>-м столбце. Таким образом, после <math>n-1</math> шагов преобразований получается матрица <math>R</math> из <math>QR</math>-разложения. | ||
| − | + | На каждом из шагов метода матрицу отражений обычно представляют не в стандартном виде, а в виде <math>A=E-\frac{1}{\gamma}vv^*</math>, где <math>v</math> находится через координаты текущего i-го столбца <math>s</math> так: | |
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
Версия 09:25, 10 марта 2016
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
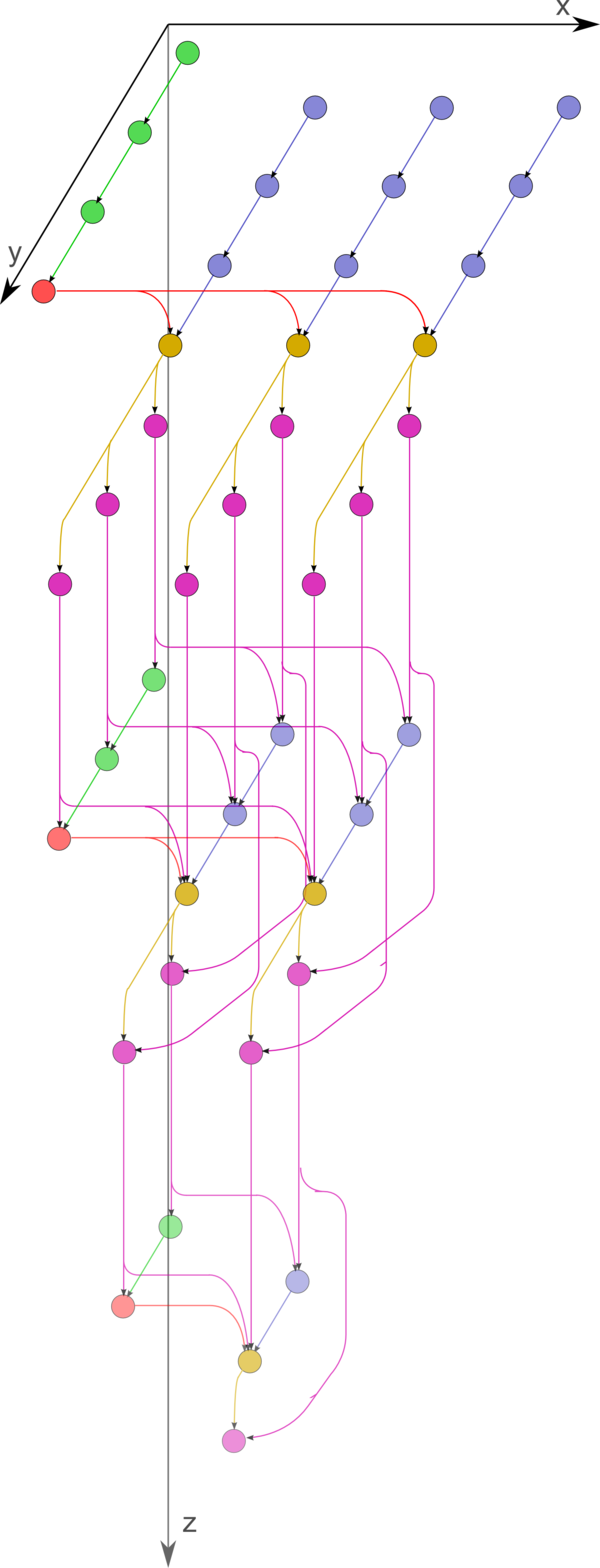
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Хаусхолдера (в советской математической литературе называется также методом отражений) используется для разложения матриц в виде [math]A=QR[/math] ([math]Q[/math] - унитарная, [math]R[/math] — правая треугольная матрица)[1]. При этом матрица [math]Q[/math] хранится и используется не в своём явном виде, а в виде произведения матриц отражения[2]. Каждая из матриц отражения может быть определена одним вектором. Это позволяет в классическом исполнении метода отражений хранить результаты разложения на месте матрицы A с использованием минимального одномерного дополнительного массива.
1.2 Математическое описание алгоритма
В методе Хаусхолдера для выполнения [math]QR[/math]-разложения матрицы используются умножения её слева на матрицы Хаусхолдера (отражений).
Матрица отражений (Хаусхолдера) - матрица вида [math]U=E-2ww^*[/math], где [math]w[/math] - вектор, удовлетворяющий равенству [math]w^{*}w=1[/math]. Является одновременно унитарной ([math]U^{*}U=E[/math]) и эрмитовой ([math]U^{*}=U[/math]), поэтому обратна самой себе ([math]U^{-1}=U[/math]).
На [math]i[/math]-м шаге метода с помощью преобразования отражения "убираются" ненулевые поддиагональные элементы в [math]i[/math]-м столбце. Таким образом, после [math]n-1[/math] шагов преобразований получается матрица [math]R[/math] из [math]QR[/math]-разложения.
На каждом из шагов метода матрицу отражений обычно представляют не в стандартном виде, а в виде [math]A=E-\frac{1}{\gamma}vv^*[/math], где [math]v[/math] находится через координаты текущего i-го столбца [math]s[/math] так: