|
|
| Строка 1: |
Строка 1: |
| − | = Поиск кратчайшего пути от одной вершины (SSSP) = | + | {{algorithm |
| − | == Постановка задачи == | + | | name = Разложение Холецкого |
| | + | | serial_complexity = <math>O(n^3)</math> |
| | + | | pf_height = <math>O(n)</math> |
| | + | | pf_width = <math>O(n^2)</math> |
| | + | | input_data = <math>\frac{n (n + 1)}{2}</math> |
| | + | | output_data = <math>\frac{n (n + 1)}{2}</math> |
| | + | }} |
| | | | |
| − | Пусть задан граф <math>G = (V, E)</math> с весами рёбер <math>f(e)</math> и выделенной вершиной-источником <math>u</math>. Последовательность <math>P(u, v)</math> рёбер <math>e_1 = (u, w_1)</math>, <math>e_2 = (w_1, w_2)</math>, …, <math>e_k = (w_{k-1}, v)</math> называется ''путём'', идущим от вершины <math>u</math> к вершине <math>v</math>. Суммарный вес этого пути равен
| + | == Свойства и структура алгоритма == |
| | | | |
| − | :<math>
| + | === Общее описание алгоритма === |
| − | f(P(u, v)) = \sum_{i = 1}^k f(e_i).
| |
| − | </math>
| |
| − |
| |
| − | Требуется для каждой вершины <math>v</math>, достижимой из вершины-источника <math>u</math>, указать путь <math>P^*(u, v)</math>, имеющий наименьший возможный суммарный вес:
| |
| − | | |
| − | :<math>
| |
| − | f^*(v) = f(P^*(u, v)) = \min f(P(u, v)).
| |
| − | </math>
| |
| − | | |
| − | Название задачи на английском языке – «Single Source Shortest Path» (SSSP).
| |
| − | | |
| − | == Варианты задачи ==
| |
| | | | |
| − | Если требуется найти кратчайшие пути не от одной, а от всех вершин - см. [[Поиск кратчайшего пути для всех пар вершин (APSP)|поиск кратчайшего пути для всех пар вершин]].
| + | '''Разложение Холецкого''' впервые предложено французским офицером и математиком Андре-Луи Холецким в конце Первой Мировой войны, незадолго до его гибели в бою в августе 1918 г. Идея этого разложения была опубликована в 1924 г. его сослуживцем<ref>Commandant Benoit, Note sur une méthode de résolution des équations normales provenant de l'application de la méthode des moindres carrés à un système d'équations linéaires en nombre inférieur à celui des inconnues (Procédé du Commandant Cholesky), Bulletin Géodésique 2 (1924), 67-77.</ref>. Потом оно было использовано поляком Т. Банашевичем<ref>Banachiewicz T. Principles d'une nouvelle technique de la méthode des moindres carrês. Bull. Intern. Acad. Polon. Sci. A., 1938, 134-135.</ref><ref>Banachiewicz T. Méthode de résoltution numérique des équations linéaires, du calcul des déterminants et des inverses et de réduction des formes quardatiques. Bull. Intern. Acad. Polon. Sci. A., 1938, 393-401.</ref> в 1938 г. В советской математической литературе называется также методом квадратного корня<ref>Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.</ref><ref>Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.</ref><ref>Фаддеев Д.К., Фаддева В.Н. Вычислительные основы линейной алгебры. М.-Л.: Физматгиз, 1963.</ref>; название связано с характерными операциями, отсутствующими в родственном разложении Гаусса. |
| | | | |
| − | Задача может быть поставлена как для ориентированного, так и для неориентированного графа. Приведённая постановка задачи применима в обоих случаях.
| + | Первоначально разложение Холецкого использовалось исключительно для плотных симметричных положительно определенных матриц. В настоящее время его использование гораздо шире. Оно может быть применено также, например, к эрмитовым матрицам. Для повышения производительности вычислений часто применяется блочная версия разложения. |
| | | | |
| − | В зависимости от ограничений на возможные значения весов различают следующие случаи. | + | Для разреженных матриц разложение Холецкого также широко применяется в качестве основного этапа прямого метода решения линейных систем. В этом случае используют специальные упорядочивания для уменьшения ширины профиля исключения, а следовательно и уменьшения количества арифметических операций. Другие упорядочивания используются для выделения независимых блоков вычислений при работе на системах с параллельной организацией. |
| | | | |
| − | * '''Единичные веса'''. В этом случае задача существенно упрощается и может быть решена за линейное время [[Поиск в ширину (BFS)|алгоритмом поиска вширь]].
| + | Варианты разложения Холецкого нашли успешные применения и в итерационных методах для построения переобусловливателей разреженных симметричных положительно определенных матриц. В неполном треугольном разложении («по позициям») элементы переобусловливателя вычисляются только в заранее заданных позициях, например, в позициях ненулевых элементов исходной матрицы (так называемое разложение IC0). Для получения же более точного разложения применяется приближение, в котором фильтрация малых элементов производится «по значениям». В зависимости от используемого порога фильтрации можно получить более точное, но и более заполненное разложение. Существует и алгоритм разложения второго порядка точности<ref>Kaporin I.E. High quality preconditioning of a general symmetric positive definite matrix based on its UTU + UTR + RTU-decomposition. Numer. Lin. Algebra Appl. (1998) Vol. 5, No. 6, 483-509.</ref>. В нём при таком же заполнении множителей разложения удается улучшить точность. Для такого разложения в параллельном режиме используется специальный вариант аддитивного переобуславливания на основе разложения второго порядка<ref>Капорин И.Е., Коньшин И.Н. Параллельное решение симметричных положительно-определенных систем на основе перекрывающегося разбиения на блоки. Ж. вычисл. матем. и матем. физ., 2001, Т, 41, N. 4, C. 515–528.</ref>. |
| − | * '''Положительные целые веса'''. Задача также может быть решена за линейное время<ref name=thorup>Thorup, Mikkel. “Undirected Single-Source Shortest Paths with Positive Integer Weights in Linear Time.” Journal of the ACM 46, no. 3 (May 1, 1999): 362–94. doi:10.1145/316542.316548.</ref> (хотя и с большей константой).
| |
| − | * '''Неотрицательные веса'''. Часто встречающееся на практике ограничение, когда вес ребра соответствует времени или стоимости прохождения участка маршрута и не может быть отрицательным.
| |
| − | * '''Произвольные веса'''. Наиболее общая постановка. Граф не должен содержать циклов с отрицательным суммарным весом, иначе кратчайшего пути не существует.
| |
| | | | |
| − | == Свойства задачи ==
| + | На этой странице представлено исходное разложение Холецкого с новых позиций нашего суперкомпьютерного века. Приведено описание конкретной версии разложения Холецкого — для плотных вещественных симметричных положительно определённых матриц, но структура для ряда других версий, например, для комплексного случая, почти такая же, различия состоят в замене большинства вещественных операций на комплексные. Список остальных основных вариантов разложения можно посмотреть на странице [[Метод Холецкого (нахождение симметричного треугольного разложения)]]. |
| | | | |
| − | Решение задачи удовлетворяет принципу оптимальности: если путь <math>P^*(u, w)</math> является частью кратчайшего пути <math>P^*(u, v)</math>, то <math>P^*(u, w)</math> является кратчайшим путём от источника <math>u</math> до вершины <math>w</math>.
| + | Используется для разложения положительно определённых эрмитовых (''в вещественном случае - симметрических'') матриц в виде <math>A = L L^*</math> (<math>L</math> — [http://lineal.guru.ru/lineal3/texts.php?PHPSESSID=e8862lf95ipuht6hb7bd6vl1m6&&rd=3368 нижняя треугольная матрица]) или в виде <math>A = U^* U</math> (<math>U</math> — [http://lineal.guru.ru/lineal3/texts.php?PHPSESSID=e8862lf95ipuht6hb7bd6vl1m6&&rd=3368 верхняя треугольная матрица] ; эти разложения совершенно эквивалентны друг другу по вычислениям и различаются только способом представления данных). Он заключается в реализации формул для элементов матрицы <math>L</math>, получающихся из вышеприведённого равенства единственным образом. Получило широкое распространение благодаря следующим особенностям. |
| | | | |
| − | Принцип оптимальности означает, что для каждой вершины <math>v</math> вместо всего кратчайшего пути <math>P^*(u, v)</math> достаточно хранить его последнее ребро <math>e^*_v</math>. Отсюда следует оценка объёма памяти <math>O(m)</math>.
| + | ==== Симметричность и положительная определённость матрицы ==== |
| | | | |
| − | == Описание входных и выходных данных ==
| + | Симметричность матрицы позволяет хранить и вычислять только чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций в сравнении с, например, разложением по методу Гаусса. При этом альтернативное (без вычисления квадратных корней) LU-разложение, использующее симметрию матрицы, всё же несколько быстрее метода Холецкого (не использует извлечение квадратных корней), но требует хранения всей матрицы. |
| | + | Благодаря тому, что разлагаемая матрица не только симметрична, но и положительно определена, её LU-разложения, в том числе и разложение методом Холецкого, имеют наименьшее ''[[Глоссарий#Эквивалентное возмущение|эквивалентное возмущение]]'' из всех известных разложений матриц. |
| | | | |
| − | '''Входные данные''': взвешенный граф <math>(V, E, W)</math> (<math>n</math> вершин <math>v_i</math> и <math>m</math> рёбер <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math> с весами <math>f_j</math>), вершина-источник <math>u</math>.
| + | ==== Режим накопления ==== |
| | | | |
| − | '''Объём входных данных''': <math>O(m + n)</math>. | + | Алгоритм позволяет использовать так называемый ''режим накопления'', обусловленный тем, что значительную часть вычислений составляют ''вычисления скалярных произведений''. |
| | | | |
| − | '''Выходные данные''' (возможные варианты):
| + | === Математическое описание алгоритма === |
| − | # для каждой вершины <math>v</math> исходного графа – последнее ребро <math>e^*_v = (w, v)</math>, лежащее на кратчайшем пути от вершины <math>u</math> к <math>v</math>, или соответствующая вершина <math>w</math>;
| |
| − | # для каждой вершины <math>v</math> исходного графа – суммарный вес <math>f^*(v)</math> кратчайшего пути от от вершины <math>u</math> к <math>v</math>.
| |
| − |
| |
| − | '''Объём выходных данных''': <math>O(n)</math>.
| |
| | | | |
| − | === Преобразование выходных данных и поиск кратчайшего пути ===
| + | Исходные данные: положительно определённая симметрическая матрица <math>A</math> (элементы <math>a_{ij}</math>). |
| | | | |
| − | Кратчайший путь от <math>u</math> к <math>v</math> может быть восстановлен за время <math>O(\left |P^*(u, v) \right |)</math>, если, начиная с вершины <math>v</math>, проходить рёбра <math>e^*_w</math> в обратном направлении до тех пор, пока не будет посещена вершина <math>u</math>.
| + | Вычисляемые данные: нижняя треугольная матрица <math>L</math> (элементы <math>l_{ij}</math>). |
| | | | |
| − | Рёбра <math>e^*_v</math> могут быть восстановлены за время <math>O(m)</math> перебором рёбер для каждой вершины:
| + | Формулы метода: |
| | :<math> | | :<math> |
| − | e^*_v \in \{ (w, v) \in E \mid f^*(v) = f^*(w) + f((v, w)) \}.
| + | \begin{align} |
| | + | l_{11} & = \sqrt{a_{11}}, \\ |
| | + | l_{j1} & = \frac{a_{j1}}{l_{11}}, \quad j \in [2, n], \\ |
| | + | l_{ii} & = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}, \quad i \in [2, n], \\ |
| | + | l_{ji} & = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}, \quad i \in [2, n - 1], j \in [i + 1, n]. |
| | + | \end{align} |
| | </math> | | </math> |
| − | Перебор может осуществляться параллельно.
| |
| | | | |
| − | Для поиска кратчайших расстояний <math>f^*(v)</math> по набору рёбер <math>e^*_v</math>, необходимо построить из них дерево, на котором выполнить [[Поиск в ширину (BFS)|поиск в ширину]] за время <math>O(m)</math> (с возможностью параллелизации).
| + | Существует также блочная версия метода, однако в данном описании разобран только точечный метод. |
| | | | |
| − | == Алгоритмы решения задачи ==
| + | В ряде реализаций деление на диагональный элемент выполняется в два этапа: вычисление <math>\frac{1}{l_{ii}}</math> и затем умножение на него всех (видоизменённых) <math>a_{ji}</math> . Здесь мы этот вариант алгоритма не рассматриваем. Заметим только, что он имеет худшие параллельные характеристики, чем представленный. |
| | | | |
| − | * '''[[Поиск в ширину (BFS)]]''' для ориентированных невзвешенных графов, сложность <math>O(m)</math>.
| + | === Вычислительное ядро алгоритма === |
| − | * '''[[Алгоритм Дейкстры]]'''<ref>Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.</ref><ref>Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1, 1987): 596–615. doi:10.1145/28869.28874.</ref> для ориентированных графов с неотрицательными весами, сложность <math>O(m + n \ln n)</math>.
| |
| − | * '''[[Алгоритм Беллмана-Форда]]'''<ref>Bellman, Richard. “On a Routing Problem.” Quarterly of Applied Mathematics 16 (1958): 87–90.</ref><ref>Ford, L R. Network Flow Theory. Rand.org, RAND Corporation, 1958.</ref><ref>Moore, Edward F. “The Shortest Path Through a Maze,” International Symposium on the Theory of Switching, 285–92, 1959.</ref> для ориентированных графов с произвольными весами, сложность <math>O(mn)</math>.
| |
| − | * '''[[Алгоритм Δ-шагания]]'''<ref>Meyer, U, and P Sanders. “Δ-Stepping: a Parallelizable Shortest Path Algorithm.” Journal of Algorithms 49, no. 1 (October 2003): 114–52. doi:10.1016/S0196-6774(03)00076-2.</ref> для ориентированных графов с неотрицательными весами, средняя сложность на графах со случайными весами <math>O(n + m + dL)</math>, параллельная сложность <math>O((dL + \ln n) \ln n</math> со средней работой <math>O(n + m + dL \ln n)</math>.
| |
| − | * '''Алгоритм Торупа'''<ref name=thorup /> представляет собой теоретическое доказательство возможности решения задачи для неориентированных графов с положительными целыми весами за линейное время <math>O(m)</math>.
| |
| − | * В ориентированном ациклическом графе с произвольными весами время поиска кратчайших путей линейное – <math>O(m + n)</math>, алгоритм основан на топологической сортировке графа.
| |
| | | | |
| − | Обозначения: <math>m</math> – число рёбер, <math>n</math> – число вершин, <math>d</math> – максимальная степень вершины, <math>L</math> – максимальный суммарный вес кратчайшего пути.
| + | Вычислительное ядро последовательной версии метода Холецкого можно составить из множественных (всего их <math>\frac{n (n - 1)}{2}</math>) вычислений скалярных произведений строк матрицы: |
| | | | |
| − | Перечисленные алгоритмы могут использоваться и для решения [[Поиск кратчайшего пути для всех пар вершин (APSP)|задачи поиска кратчайшего пути для всех пар вершин графа]] (для этого необходимо запустить соответствующий алгоритм для каждой вершины графа, что при необходимости можно сделать параллельно), при этом оценка сложности умножается на <math>n</math>.
| + | :<math>\sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math> |
| | | | |
| | + | в режиме накопления или без него, в зависимости от требований задачи. Во многих последовательных реализациях упомянутый способ представления не используется. Дело в том, что в них вычисление сумм типа |
| | | | |
| − | = Поиск кратчайшего пути для всех пар вершин (APSP) = | + | :<math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math><nowiki/> |
| | | | |
| − | == Постановка задачи ==
| + | в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода не вычисления скалярных произведений, а вычисления выражений |
| | | | |
| − | Пусть задан граф <math>G = (V, E)</math> с весами рёбер <math>f(e)</math>, <math>e \in E</math>. Последовательность <math>P(u, v)</math> рёбер <math>e_1 = (u, w_1)</math>, <math>e_2 = (w_1, w_2)</math>, …, <math>e_k = (w_{k-1}, v)</math> называется ''путём'', идущим от вершины <math>u</math> к вершине <math>v</math>. Вершина <math>v</math> называется ''достижимой'' из вершины <math>u</math>, если существует хотя бы один путь <math>P(u, v)</math>. Суммарный вес этого пути равен
| + | :<math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math> |
| | | | |
| − | :<math>
| + | в ''режиме накопления'' или без него. |
| − | f(P(u, v)) = \sum_{i = 1}^k f(e_i).
| |
| − | </math>
| |
| − |
| |
| − | Требуется для каждой пары вершины <math>(u, v)</math>, для которой вершина <math>v</math> достижима из вершины <math>u</math>, указать путь <math>P^*(u, v)</math>, имеющий наименьший возможный суммарный вес:
| |
| | | | |
| − | :<math>
| + | Тем не менее, в популярных зарубежных реализациях точечного метода Холецкого, в частности, в библиотеках LINPACK и LAPACK, основанных на BLAS, используются именно вычисления скалярных произведений в виде вызова соответствующих подпрограмм BLAS (конкретно — функции SDOT). На последовательном уровне это влечёт за собой дополнительную операцию суммирования на каждый из <math>\frac{n (n + 1)}{2}</math> вычисляемый элемент матрицы <math>L</math> и некоторое замедление работы программы (о других следствиях рассказано ниже в разделе «[[#Существующие реализации алгоритма|Существующие реализации алгоритма]]»). Поэтому в данных вариантах ядром метода Холецкого будут вычисления этих скалярных произведений. |
| − | f^*(u, v) = f(P^*(u, v)) = \min f(P(u, v)).
| |
| − | </math> | |
| − |
| |
| − | Название задачи на английском языке – «All Pairs Shortest Path» (APSP).
| |
| | | | |
| − | == Варианты задачи == | + | === Макроструктура алгоритма === |
| | | | |
| − | Если требуется найти кратчайшие пути лишь от одной, а не от всех вершин – см. [[Поиск кратчайшего пути от одной вершины (SSSP)|поиск кратчайшего пути от одной вершины]].
| + | Как записано и в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть метода составляют множественные (всего <math>\frac{n (n - 1)}{2}</math>) вычисления сумм |
| | | | |
| − | Задача может быть поставлена как для ориентированного, так и для неориентированного графа. Приведённая постановка задачи применима в обоих случаях.
| + | :<math>a_{ji}-\sum_{p=1}^{i-1}l_{ip} l_{jp}</math> |
| | | | |
| − | В зависимости от ограничений на возможные значения весов различают следующие случаи.
| + | в режиме накопления или без него. |
| | | | |
| − | * '''Единичные веса'''. В этом случае задача существенно упрощается и может быть решена за квадратичное время [[Поиск в ширину (BFS)|алгоритмом поиска вширь]].
| + | === Схема реализации последовательного алгоритма === |
| − | * '''Положительные целые веса'''. Задача также может быть решена за квадратичное время<ref name=thorup>Thorup, Mikkel. “Undirected Single-Source Shortest Paths with Positive Integer Weights in Linear Time.” Journal of the ACM 46, no. 3 (May 1, 1999): 362–94. doi:10.1145/316542.316548.</ref> (хотя и с большей константой).
| |
| − | * '''Неотрицательные веса'''. Часто встречающееся на практике ограничение, когда вес ребра соответствует времени или стоимости прохождения участка маршрута и не может быть отрицательным.
| |
| − | * '''Произвольные веса'''. Наиболее общая постановка. Граф не должен содержать циклов с отрицательным суммарным весом, иначе кратчайшего пути не существует.
| |
| | | | |
| − | В зависимости от способа организации вычислений возможны следующие варианты:
| + | Последовательность исполнения метода следующая: |
| | | | |
| − | * статический граф, полное вычисление всех кратчайших путей (классический подход);
| + | 1. <math>l_{11}= \sqrt{a_{11}}</math> |
| − | * вычисление онлайн<ref>Djidjev, Hristo N, Grammati E Pantziou, and Christos D Zaroliagis. “On-Line and Dynamic Algorithms for Shortest Path Problems.” In Proceedings of STACS 95, 193–204. Lecture Notes in Computer Science Vol. 900, Berlin, Heidelberg: Springer, 1995. doi:10.1007/3-540-59042-0_73.</ref>: производятся предварительные вычисления, далее путь между парой вершин вычисляется по запросу (такой подход уместен, если в реальности потребуется вычислить кратчайшие пути только для некоторых пар, но заранее набор этих пар неизвестен);
| |
| − | * динамический граф<ref>Demetrescu, Camil, and Giuseppe F Italiano. “Fully Dynamic All Pairs Shortest Paths with Real Edge Weights.” Journal of Computer and System Sciences 72, no. 5 (August 2006): 813–37. doi:10.1016/j.jcss.2005.05.005.</ref>: рёбра и вершины могут добавляться и удаляться, при этом происходит пересчёт кратчайших расстояний (вариант подходит для постоянно меняющихся графов, например, для социальных сетей).
| |
| | | | |
| − | == Описание входных и выходных данных == | + | 2. <math>l_{j1}= \frac{a_{j1}}{l_{11}}</math> (при <math>j</math> от <math>2</math> до <math>n</math>). |
| | | | |
| − | '''Входные данные''': взвешенный граф <math>(V, E, W)</math> (<math>n</math> вершин <math>v_i</math> и <math>m</math> рёбер <math>e_j = (v^{(1)}_{j}, v^{(2)}_{j})</math> с весами <math>f_j</math>).
| + | Далее для всех <math>i</math> от <math>2</math> до <math>n</math> по нарастанию выполняются |
| | | | |
| − | '''Объём входных данных''': <math>O(m + n)</math>.
| + | 3. <math>l_{ii} = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}</math> и |
| | | | |
| − | '''Выходные данные''' (возможные варианты):
| + | 4. (кроме <math>i = n</math>): <nowiki/><math>l_{ji} = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}</math> (для всех <math>j</math> от <math>i + 1</math> до <math>n</math>). |
| − | # для каждой пары вершины <math>(u, v)</math> исходного графа – последнее ребро <math>e^*_{uv} = (w, v)</math>, лежащее на кратчайшем пути от вершины <math>u</math> к <math>v</math>, или соответствующая вершина <math>w</math>;
| |
| − | # для каждой пары вершин <math>(u, v)</math> исходного графа – суммарный вес <math>f^*(u, v)</math> кратчайшего пути от от вершины <math>u</math> к <math>v</math>.
| |
| − |
| |
| − | '''Объём выходных данных''': <math>O(n^2)</math>.
| |
| | | | |
| − | === Преобразование выходных данных и поиск кратчайшего пути ===
| + | После этого (если <math>i < n</math>) происходит переход к шагу 3 с бо́льшим <math>i</math>. |
| | | | |
| − | Кратчайший путь от <math>u</math> к <math>v</math> может быть восстановлен за время <math>O(\left |P^*(u, v) \right |)</math>, если, начиная с вершины <math>v</math>, проходить рёбра <math>e^*_{uw}</math> в обратном направлении до тех пор, пока не будет посещена вершина <math>u</math>.
| + | Особо отметим, что вычисления сумм вида <math>a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}</math> в обеих формулах производят в режиме накопления вычитанием из <math>a_{ji}</math> произведений <math>l_{ip} l_{jp}</math> для <math>p</math> от <math>1</math> до <math>i - 1</math>, c нарастанием <math>p</math>. |
| | | | |
| − | Рёбра <math>e^*_{uv}</math> могут быть восстановлены за время <math>O(mn)</math> перебором рёбер для каждой вершины:
| + | === Последовательная сложность алгоритма === |
| − | :<math>
| |
| − | e^*_{uv} \in \{ (w, v) \in E \mid f^*(u, v) = f^*(u, w) + f((v, w)) \}.
| |
| − | </math>
| |
| − | Перебор может осуществляться параллельно.
| |
| | | | |
| − | Для поиска кратчайших расстояний <math>f^*(u, v)</math> по набору рёбер <math>e^*_{uv}</math>, необходимо для данной вершины <math>u</math> построить дерево из рёбер <math>e^*_{uv}</math> и выполнить на нём [[Поиск в ширину (BFS)|поиск в ширину]] за время <math>O(m)</math> (с возможностью параллелизации), общее время для всех пар вершин – <math>O(mn)</math>. | + | Для разложения матрицы порядка n методом Холецкого в последовательном (наиболее быстром) варианте требуется: |
| | + | |
| | + | * <math>n</math> вычислений квадратного корня, |
| | + | * <math>\frac{n(n-1)}{2}</math> делений, |
| | + | * <math>\frac{n^3-n}{6}</math> сложений (вычитаний), |
| | + | * <math>\frac{n^3-n}{6}</math> умножений. |
| | | | |
| − | == Алгоритмы решения задачи ==
| + | Умножения и сложения (вычитания) составляют ''основную часть алгоритма''. |
| | + | |
| | + | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения метода Холецкого. |
| | | | |
| − | * '''[[Алгоритм Джонсона]]'''<ref>Johnson, Donald B. “Efficient Algorithms for Shortest Paths in Sparse Networks.” Journal of the ACM 24, no. 1 (January 1977): 1–13. doi:10.1145/321992.321993.</ref> для ориентированных графов с произвольными весами, сложность <math>O(mn+ n^2 \ln n)</math>.
| + | При классификации по последовательной сложности, таким образом, метод Холецкого относится к алгоритмам ''с кубической сложностью''. |
| − | * '''[[Алгоритм Флойда-Уоршелла]]'''<ref>Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.</ref><ref>Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.</ref><ref>Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.</ref> для ориентированных графов с произвольными весами, сложность <math>O(n^3)</math>.
| |
| − | * Многократное применение любого алгоритма [[Поиск кратчайшего пути от одной вершины (SSSP)|поиска кратчайшего пути от одной вершины]]:
| |
| − | ** '''[[Поиск в ширину (BFS)]]''' для ориентированных невзвешенных графов, сложность <math>O(mn)</math>.
| |
| − | ** '''[[Алгоритм Дейкстры]]'''<ref>Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.</ref><ref>Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1, 1987): 596–615. doi:10.1145/28869.28874.</ref> для ориентированных графов с неотрицательными весами, сложность <math>O(mn + n^2 \ln n)</math>.
| |
| − | ** '''[[Алгоритм Беллмана-Форда]]'''<ref>Bellman, Richard. “On a Routing Problem.” Quarterly of Applied Mathematics 16 (1958): 87–90.</ref><ref>Ford, L R. Network Flow Theory. Rand.org, RAND Corporation, 1958.</ref><ref>Moore, Edward F. “The Shortest Path Through a Maze,” International Symposium on the Theory of Switching, 285–92, 1959.</ref> для ориентированных графов с произвольными весами, сложность <math>O(mn^2)</math>.
| |
| − | ** '''[[Алгоритм Δ-шагания]]'''<ref>Meyer, U, and P Sanders. “Δ-Stepping: a Parallelizable Shortest Path Algorithm.” Journal of Algorithms 49, no. 1 (October 2003): 114–52. doi:10.1016/S0196-6774(03)00076-2.</ref> для ориентированных графов с неотрицательными весами, средняя сложность на графах со случайными весами <math>O(n(n + m + dL))</math>, параллельная сложность <math>O((dL + \ln n) n \ln n</math> со средней работой <math>O(n (n + m + dL \ln n))</math>.
| |
| − | ** '''Алгоритм Торупа'''<ref name=thorup /> представляет собой теоретическое доказательство возможности решения задачи для неориентированных графов с положительными целыми весами за линейное время <math>O(mn)</math>.
| |
| − | ** В ориентированном ациклическом графе с произвольными весами алгоритм основан на топологической сортировке графа, сложность <math>O(mn)</math>.
| |
| | | | |
| − | Обозначения: <math>m</math> – число рёбер, <math>n</math> – число вершин, <math>d</math> – максимальная степень вершины, <math>L</math> – максимальный суммарный вес кратчайшего пути.
| + | === Информационный граф === |
| | | | |
| − | == Ресурс параллелизма ==
| + | Опишем [[глоссарий#Граф алгоритма|граф алгоритма]]<ref>Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.</ref><ref>Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.</ref><ref>Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.</ref> как аналитически, так и в виде рисунка. |
| | | | |
| − | Задача может быть решена путём применения любого алгоритма [[Поиск кратчайшего пути от одной вершины (SSSP)|поиска кратчайшего пути от одной вершины]] для всех вершин графа, при этом вычисления для различных вершин независимы и могут выполняться параллельно.
| + | Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности. |
| | | | |
| − | В связи с квадратичной сложностью выходных данных и более чем квадратичной сложностью вычислений, имеет смысл проводить предварительную обработку данных и использовать различные декомпозиции графа, сводя задачу к параллельному нахождению кратчайших путей на подграфах меньших размеров<ref>Banerjee, Dip Sankar, Ashutosh Kumar, Meher Chaitanya, Shashank Sharma, and Kishore Kothapalli. “Work Efficient Parallel Algorithms for Large Graph Exploration on Emerging Heterogeneous Architectures.” Journal of Parallel and Distributed Computing, December 2014. doi:10.1016/j.jpdc.2014.11.006.</ref>:
| + | '''Первая''' группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT. |
| − | * [[Алгоритм Шилоаха-Вишкина поиска компонент связности|выделение компонент связности]];
| + | Единственная координата каждой из вершин <math>i</math> меняется в диапазоне от <math>1</math> до <math>n</math>, принимая все целочисленные значения. |
| − | * [[Алгоритм Тарьяна поиска «мостов» в графе|выделение подграфов, связанных только «мостами»]] (рёбрами, удаление которых нарушает связность графа);
| |
| − | * [[Алгоритм Тарьяна поиска компонент двусвязности|выделение компонент двусвязности]], связанных только «шарнирами» (другие названия – «точки сочленения» и «разделяющие вершины»; вершины, удаление которых нарушает связность графа);
| |
| − | * удаление «висящих» вершин (вершины, имеющие не более одной соседней вершины в графе).
| |
| | | | |
| − | Набор декомпозиций, который целесообразно использовать в конкретном случае, зависит от структуры графа и может быть определён только после её анализа.
| + | Аргумент этой функции |
| − | | + | |
| − | | + | * при <math>i = 1</math> — элемент ''входных данных'', а именно <math>a_{11}</math>; |
| − | = Поиск транзитивного замыкания орграфа =
| + | * при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1</math>, <math>i</math>, <math>i - 1</math>. |
| − | | + | Результат срабатывания операции является ''выходным данным'' <math>l_{ii}</math>. |
| − | == Постановка задачи ==
| |
| − | | |
| − | Пусть задан ориентированный граф <math>G = (V, E)</math>. Последовательность <math>P(u, v)</math> рёбер <math>e_1 = (u, w_1)</math>, <math>e_2 = (w_1, w_2)</math>, …, <math>e_k = (w_{k-1}, v)</math> называется ''путём'', идущим от вершины <math>u</math> к вершине <math>v</math>. Вершина <math>v</math> называется ''достижимой'' из вершины <math>u</math>, если существует хотя бы один путь <math>P(u, v)</math>. Каждая вершина достижима сама из себя.
| |
| − | | |
| − | Требуется построить '''транзитивное замыкание''' <math>G^+ = (V, E^+)</math> графа <math>G</math>: ребро <math>(v, w) \in E^+</math> тогда и только тогда, когда в графе <math>G</math> вершина <math>w</math> достижима из вершины <math>v</math>.
| |
| − | | |
| − | Эквивалентная формулировка: для данного рефлексивного бинарного отношения <math>R</math> требуется построить наименьшее по включению отношение <math>R^+</math>, содержащее <math>R</math> и облагающее свойством транзитивности: если <math>aR^+b</math> и <math>bR^+c</math>, то <math>aR^+c</math>. Если исходное отношение <math>R</math> было симметричным, то <math>R^+</math> будет отношением эквивалентности и тогда достаточно найти его классы эквивалентности.
| |
| − | | |
| − | == Свойства задачи ==
| |
| − | | |
| − | Если вершины <math>v</math> и <math>w</math> принадлежат одной [[Связность в графах|компоненте сильной связности]] графа <math>G</math>, то транзитивное замыкание содержит рёбра <math>(v, w)</math> и <math>(w, v)</math>. В неориентированном графе ребро <math>(v, w)</math> принадлежит транзитивному замыканию в том и только в том случае, когда вершины <math>v</math> и <math>w</math> принадлежат одной и той же компоненте связности. Следовательно, для неориентированного графа поиск транзитивного замыкания эквивалентен поиску компонент связности.
| |
| − | | |
| − | Если вершины <math>x</math> и <math>y</math> принадлежат одной компоненте сильной связности графа <math>G</math>, а вершины <math>z</math> и <math>t</math> – другой, то рёбра <math>(x, z)</math>, <math>(x, t)</math>, <math>(y, z)</math>, <math>(y, t)</math> принадлежат или не принадлежат транзитивному замыканию <math>G^+</math> одновременно. Следовательно, поиск транзитивного замыкания графа <math>G</math> можно свести к поиску транзитивного замыкания ациклического графа, полученного из <math>G</math> схлопыванием каждой компоненты сильной связности в одну вершину; на этом принципе основан [[алгоритм Пурдома]].
| |
| − | | |
| − | Граф <math>G</math> и его транзитивное замыкание <math>G^+</math> имеют одни и те же компоненты сильной связности (в терминах вершин).
| |
| − | | |
| − | == Алгоритмы решения задачи ==
| |
| − | | |
| − | В '''неориентированном''' графе вершина <math>w</math> достижима из вершины <math>v</math> тогда и только тогда, когда они обе принадлежат одной и той же компоненте связности. Транзитивное замыкание сводится к поиску [[Связность в графах|компонент связности]] графа и может быть найдено следующими алгоритмами:
| |
| − | * последовательным применением алгоритма [[Поиск в ширину (BFS)|поиска в ширину]] за время <math>O(m)</math>;
| |
| − | * с помощью [[Система непересекающихся множеств|системы непересекающихся множеств]]<ref>Tarjan, Robert Endre. “Efficiency of a Good but Not Linear Set Union Algorithm.” Journal of the ACM 22, no. 2 (April 1975): 215–25. doi:10.1145/321879.321884.</ref> за время <math>O(m \alpha(m, n))</math>, с возможностью эффективной многопоточной реализации<ref>Anderson, Richard J, and Heather Woll. “Wait-Free Parallel Algorithms for the Union-Find Problem,” 370–80, New York, New York, USA: ACM Press, 1991. doi:10.1145/103418.103458.</ref>; | |
| − | * параллельным алгоритмом [[Алгоритм Шилоаха-Вишкина поиска компонент связности|Шилоаха-Вишкина]]<ref>Shiloach, Yossi, and Uzi Vishkin. “An <math>O(\log n)</math> Parallel Connectivity Algorithm.” Journal of Algorithms 3, no. 1 (March 1982): 57–67. doi:10.1016/0196-6774(82)90008-6.</ref> за время <math>O(\ln n)</math> на <math>n + 2m</math> процессорах.
| |
| − | | |
| − | В '''ориентированном''' графе транзитивное замыкание может быть сведено к поиску кратчайших путей в графе с единичными весами и найдено следующими алгоритмами:
| |
| − | * '''[[Алгоритм Флойда-Уоршелла|алгоритм Флойда-Уоршелла]]'''<ref>Floyd, Robert W. “Algorithm 97: Shortest Path.” Communications of the ACM 5, no. 6 (June 1, 1962): 345. doi:10.1145/367766.368168.</ref><ref>Warshall, Stephen. “A Theorem on Boolean Matrices.” Journal of the ACM 9, no. 1 (January 1, 1962): 11–12. doi:10.1145/321105.321107.</ref>, сложность <math>O(n^3)</math> (первый опубликованный алгоритм поиска транзитивного замыкания<ref>Roy, Bernard. “Transitivité Et Connexité.” Comptes Rendus De l'Académie Des Sciences 249 (1959): 216–218.</ref> как раз представляет собой алгоритм Флойда-Уоршелла для графов с единичными весами);
| |
| − | * многократное применение '''[[Поиск в ширину (BFS)|поиска в ширину]]''', сложность <math>O(mn)</math>;
| |
| − | * '''[[алгоритм Пурдома]]'''<ref name=Purdom>Purdom, Paul, Jr. “A Transitive Closure Algorithm.” Bit 10, no. 1 (March 1970): 76–94. doi:10.1007/BF01940892.</ref>, сложность <math>O(m + \mu n)</math>.
| |
| − | | |
| − | Обозначения: <math>m</math> – число рёбер, <math>n</math> – число вершин, <math>\mu \le m</math> – число рёбер, соединяющих [[Связность в графах|компоненты сильной связности]].
| |
| − | | |
| − | == Ресурс параллелизма ==
| |
| − | | |
| − | Задача может быть решена путём алгоритма [[Поиск в ширину (BFS)|поиска в ширину]] для всех вершин графа, при этом вычисления для различных вершин независимы и могут выполняться параллельно.
| |
| − | | |
| − | В связи с квадратичной сложностью выходных данных и вычислений, имеет смысл проводить предварительную обработку данных и использовать различные декомпозиции графа, сводя задачу к параллельному нахождению кратчайших путей на подграфах меньших размеров<ref>Banerjee, Dip Sankar, Ashutosh Kumar, Meher Chaitanya, Shashank Sharma, and Kishore Kothapalli. “Work Efficient Parallel Algorithms for Large Graph Exploration on Emerging Heterogeneous Architectures.” Journal of Parallel and Distributed Computing, December 2014. doi:10.1016/j.jpdc.2014.11.006.</ref>:
| |
| − | * [[Алгоритм Шилоаха-Вишкина поиска компонент связности|выделение компонент связности]];
| |
| − | * [[Алгоритм Тарьяна поиска «мостов» в графе|выделение подграфов, связанных только «мостами»]] (рёбрами, удаление которых нарушает связность графа);
| |
| − | * [[Алгоритм Тарьяна поиска компонент двусвязности|выделение компонент двусвязности]], связанных только «шарнирами» (другие названия – «точки сочленения» и «разделяющие вершины»; вершины, удаление которых нарушает связность графа);
| |
| − | * удаление «висящих» вершин (вершины, имеющие не более одной соседней вершины в графе).
| |
| − | | |
| − | Набор декомпозиций, который целесообразно использовать в конкретном случае, зависит от структуры графа и может быть определён только после её анализа.
| |
| − | | |
| − | | |
| − | = Построение минимального остовного дерева (MST) =
| |
| − | | |
| − | == Постановка задачи ==
| |
| − | | |
| − | Пусть задан связный неориентированный граф <math>G = (V, E)</math> с весами рёбер <math>f(e)</math>. Подграф, являющийся деревом и проходящий через все вершины
| |
| − | <math>G</math>, называется ''основным деревом''. Остовное дерево называется ''минимальным'', если суммарный вес его рёбер является минимальным среди всех остовных
| |
| − | деревьев.
| |
| − | | |
| − | Постановка задачи и алгоритм её решения были впервые опубликованы в работе Отакара Борувки<ref name=boruvka>Borůvka, Otakar. “O Jistém Problému Minimálním.” Práce Moravské Přírodovědecké Společnosti III, no. 3 (1926): 37–58.</ref>. Английское название задачи – Minimum Spanning Tree (MST).
| |
| − | | |
| − | == Варианты задачи ==
| |
| − | | |
| − | Если исходный граф <math>G</math> несвязный, то набор минимальных остовных деревьев для всех компонент связности называется ''минимальным остовным лесом'' (Minimum
| |
| − | Spanning Forest, MSF).
| |
| − | | |
| − | Для графа с целочисленными весами возможно использование специальных приёмов, таких как [[wikipedia:ru:Поразрядная сортировка|поразрядная сортировка]], что приводит к
| |
| − | алгоритмам, решающим задачу за линейное время.
| |
| − | | |
| − | В распределённой задаче может присутствовать дополнительное требование, что обмен данными происходит только вдоль рёбер графа.
| |
| − | | |
| − | == Свойства задачи ==
| |
| − | | |
| − | '''Веса'''. Решение задачи зависит не от значений весов, а от их порядка. Таким образом, вместо задания весов можно задать порядок – предикат «меньше или равно» на множестве пар рёбер графа. По этой причине можно без ограничения общности считать, что все веса рёбер различны – для этого следует упорядочить рёбра вначале по весу, а затем по номеру. Кроме того, к исходным весам можно применить любую возрастающую функцию и это не приведёт к изменению решения. Как следствие, можно считать, что все веса находятся в заданном интервале, например, <math>[0, 1]</math>.
| |
| − | | |
| − | '''Существование и единственность'''. Минимальный опорный лес всегда существует, а если все веса рёбер различны, то он единственный. Как уже отмечалось, всегда можно сделать веса рёбер различными. Если условие различных весов не выполняется, легко построить пример, в котором будет существовать более одного минимального остовного дерева.
| |
| − | | |
| − | '''Схлопывание фрагментов'''. Пусть <math>F</math> – фрагмент минимального остовного дерева графа <math>G</math>, а граф <math>G'</math> получен из <math>G</math> склеиванием вершин, принадлежащих
| |
| − | <math>F</math>. Тогда объединение <math>F</math> и минимального остовного дерева графа <math>G'</math> даёт минимальное остовное дерево исходного графа <math>G</math>.
| |
| − | | |
| − | '''Минимальное ребро фрагмента'''. Пусть <math>F</math> – фрагмент минимального остовного дерева и <math>e_F</math> – ребро наименьшего веса, исходящее из <math>F</math> (т.е. ровно один его конец является вершиной из <math>F</math>). Если ребро <math>e_F</math> единственно, то оно принадлежит минимальному остовному дереву. На этом свойстве основаны [[алгоритм Борувки]] и [[алгоритм Прима]].
| |
| − | | |
| − | '''Минимальное ребро графа'''. Если <math>e^*</math> – единственное ребро графа с минимальным весом, то оно принадлежит минимальному остовному дереву. На этом свойстве основан [[алгоритм Крускала]].
| |
| − | | |
| − | '''Ассоциативность по рёбрам'''. Пусть <math>MSF(E)</math> – минимальный остовный лес графа с рёбрами <math>E</math>. Тогда
| |
| − | | |
| − | :<math>
| |
| − | MSF(E_1 \cup E_2 \cup \dots \cup E_k) = MSF(MSF(E_1) \cup MSF(E_2) \cup \dots \cup MSF(E_k)).
| |
| − | </math>
| |
| − | | |
| − | '''Количество рёбер''' остовного леса для графа с <math>n</math> вершинами и <math>c</math> компонентами связности равно <math>n-c</math>. Это свойство может использоваться для более быстрого завершения работы алгоритмов, если число компонент связности известно заранее.
| |
| − | | |
| − | == Описание входных и выходных данных ==
| |
| − | | |
| − | '''Входные данные''': взвешенный граф <math>(V, E, W)</math> (<math>n</math> вершин <math>v_i</math> и <math>m</math> рёбер <math>e_j = (v^{(1)}_{j},
| |
| − | v^{(2)}_{j})</math> с весами <math>f_j</math>).
| |
| − | | |
| − | '''Объём входных данных''': <math>O(m + n)</math>.
| |
| − | | |
| − | '''Выходные данные''': список рёбер минимального остовного дерева (для несвязного графа – список минимальных остовных деревьев для всех компонент связности).
| |
| − | | |
| − | '''Объём выходных данных''': <math>O(n)</math>.
| |
| − | | |
| − | == Алгоритмы решения задачи ==
| |
| − | | |
| − | Существует три классических подхода к решению задачи:
| |
| − | * '''[[Алгоритм Борувки]]''';<ref name=boruvka /><ref>Jarník, Vojtěch. “O Jistém Problému Minimálním (Z Dopisu Panu O. Borůvkovi).” Práce Moravské Přírodovědecké Společnosti 6, no. 4 (1930): 57–63.</ref>
| |
| − | * '''[[Алгоритм Крускала]]''';<ref>Kruskal, Joseph B. “On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem.” Proceedings of the American Mathematical Society 7, no. 1 (January 1956): 48–50. doi:10.1090/S0002-9939-1956-0078686-7.</ref> | |
| − | * '''[[Алгоритм Прима]]'''.<ref>Prim, R C. “Shortest Connection Networks and Some Generalizations.” Bell System Technical Journal 36, no. 6 (November 1957): 1389–1401. doi:10.1002/j.1538-7305.1957.tb01515.x.</ref><ref>Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.</ref>
| |
| − | Во всех случаях последовательная сложность алгоритма <math>O(m \ln m)</math> при использовании обычных структур данных. (Обозначения: <math>m</math> – число рёбер, <math>n</math> – число вершин.)
| |
| − | | |
| − | Все другие алгоритмы, как правило, являются вариацией на тему одного из трёх перечисленных, или их комбинацией.
| |
| − | * '''[[Алгоритм GHS]]''' (Gallager, Humblet, Spira)<ref>Gallager, Robert G, P A Humblet, and P M Spira. “A Distributed Algorithm for Minimum-Weight Spanning Trees.” ACM Transactions on Programming Languages and Systems 5, no. 1 (1983): 66–77. doi:10.1145/357195.357200.</ref> и его последующие версии<ref>Gafni, Eli. “Improvements in the Time Complexity of Two Message-Optimal Election Algorithms,” 175–85, New York, New York, USA: ACM Press, 1985. doi:10.1145/323596.323612.</ref><ref>Awerbuch, B. “Optimal Distributed Algorithms for Minimum Weight Spanning Tree, Counting, Leader Election, and Related Problems,” 230–40, New York, New York, USA: ACM Press, 1987. doi:10.1145/28395.28421.</ref> являются распределённым вариантом алгоритма Борувки. Это алгоритм обычно используется для автоматического распределённого построения остовного дерева сетью коммутаторов.
| |
| − | * '''Алгоритм Габова''' и др.<ref>Gabow, Harold N, Zvi Galil, Thomas H Spencer, and Robert Endre Tarjan. “Efficient Algorithms for Finding Minimum Spanning Trees in Undirected and Directed Graphs.” Combinatorica 6, no. 2 (June 1986): 109–22. doi:10.1007/BF02579168.</ref> использует [[wikipedia:ru:Фибоначчиева куча|фибоначчиеву кучу]] для упорядочения рёбер в алгоритме Борувки. Сложность <math>O(m \ln \beta (m, n))</math>.
| |
| − | * '''Алгоритм Фредмана и Уилларда'''<ref>Fredman, Michael L, and Dan E Willard. “Trans-Dichotomous Algorithms for Minimum Spanning Trees and Shortest Paths.” Journal of Computer and System Sciences 48, no. 3 (June 1994): 533–51. doi:10.1016/S0022-0000(05)80064-9.</ref> предназначен для графов с целочисленными весами и имеет линейную оценку сложности <math>O(m)</math>. Используется алгоритм Прима в сочетании со специально разработанным алгоритмом кучи ([[wikipedia:AF-heap|AF-heap]]).
| |
| − | * '''Алгоритм Каргера''' и др.<ref>Karger, David R, Philip N Klein, and Robert Endre Tarjan. “A Randomized Linear-Time Algorithm to Find Minimum Spanning Trees.” Journal of the ACM 42, no. 2 (March 1, 1995): 321–28. doi:10.1145/201019.201022.</ref> решает задачу ''в среднем'' за линейное время <math>O(m)</math>. (Существование детерминированного алгоритма с линейной оценкой сложности является открытым вопросом.)
| |
| − | | |
| − | Следует отметить, что алгоритмы, имеющие асимптотическую сложность лучшую, чем <math>O(m \ln n)</math>, как правило, на практике работают медленнее классических алгоритмов: константа в оценке настолько велика, что выигрыш от лучшей асимптотике будет заметен только на графах очень больших размеров.
| |
| − | | |
| − | == Ресурс параллелизма ==
| |
| − | | |
| − | # Свойства схлопывания фрагментов и минимального ребра фрагмента позволяют обрабатывать фрагменты независимо. Основанный на этих свойствах алгоритм Борувки обладает наибольшим ресурсом параллелизма среди трёх классических алгоритмов.
| |
| − | # Ассоциативность по рёбрам может быть использована для параллелизации алгоритмов Крускала и Прима, которые изначально являются существенно последовательными.
| |
| − | # Использование параллельных алгоритмов сортировки рёбер графа, либо параллельная сортировка рёбер у каждой вершины или у каждого фрагмента.
| |
| − | | |
| − | = Поиск изоморфных подграфов =
| |
| − | | |
| − | == Постановка задачи ==
| |
| − | | |
| − | Пусть заданы два графа <math>G</math> и <math>H</math>. '''Задача поиска изоморфных подграфов''' состоит в том, чтобы определить, существует ли у графа <math>G</math> подграф, изоморфный <math>H</math>, и в случае положительного ответа – предъявить хотя бы один такой подграф.
| |
| − | | |
| − | == Свойства задачи ==
| |
| − | | |
| − | Задача поиска изоморфных подграфов является NP-полной, поэтому не существует известных алгоритмов, решающих её за полиномиальное время.
| |
| − | | |
| − | == Алгоритмы решения задачи ==
| |
| − | | |
| − | '''[[Алгоритм Ульмана]]'''<ref>Ullmann, Julian R. “An Algorithm for Subgraph Isomorphism.” Journal of the ACM 23, no. 1 (January 1976): 31–42. doi:10.1145/321921.321925.</ref><ref>Ullmann, Julian R. “Bit-Vector Algorithms for Binary Constraint Satisfaction and Subgraph Isomorphism.” Journal of Experimental Algorithmics 15 (March 2010): 1.1. doi:10.1145/1671970.1921702.</ref> решает задачу поиска изоморфных подграфов за экспоненциальное время, при этом
| |
| − | * для фиксированного графа <math>H</math> время полиномиальное;
| |
| − | * для планарного графа <math>G</math> время работы линейное (при фиксированном графе <math>H</math>).
| |
| − | | |
| − | '''[[Алгоритм VF2]]'''<ref>Cordella, L P, P Foggia, C Sansone, and M Vento. “A (Sub)Graph Isomorphism Algorithm for Matching Large Graphs.” IEEE Transactions on Pattern Analysis and Machine Intelligence 26, no. 10 (October 2004): 1367–72. doi:10.1109/TPAMI.2004.75.</ref> разработан специально для применения на больших графах. | |
| − | | |
| − | = Связность в графах =
| |
| − | | |
| − | == Основные определения ==
| |
| − | | |
| − | Пусть задан (ориентированный или неориентированный) граф <math>G = (V, E)</math>. Последовательность <math>P(u, v)</math> рёбер <math>e_1 = (u, w_1)</math>, <math>e_2 = (w_1, w_2)</math>, …, <math>e_k = (w_{k-1}, v)</math> называется ''путём'', идущим от вершины <math>u</math> к вершине <math>v</math>. В этом случае вершина <math>v</math> ''достижима'' из вершины <math>u</math>. Считается, что от вершины <math>u</math> к себе самой ведёт пустой путь <math>P(u, u)</math>, то есть каждая вершина достижима из самой себя. Непустой путь <math>P(u, u)</math> называется ''циклом'' (''замкнутым обходом'').
| |
| − | | |
| − | ''Неориентированный'' граф называется ''связным'', если все его вершины достижимы из некоторой вершины (эквивалентно, из любой его вершины).
| |
| − | | |
| − | ''Ориентированный'' граф называется
| |
| − | * ''слабо связным'', если соответствующий неориентированный граф является связным;
| |
| − | * ''сильно связным'', если всякая вершина <math>v</math> достижима из любой другой вершины <math>v</math>.
| |
| − | | |
| − | ''Компонентой связности'' неориентированного графа называется максимальный по включению связный подграф.
| |
| − | | |
| − | ''Компонентой сильной связности'' ориентированного графа называется максимальный по включению сильно связный подграф. Другими словами, это подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.
| |
| − | | |
| − | ''Мостом'' в графе называется ребро, удаление которого увеличивает число компонент связности.
| |
| − | | |
| − | ''Шарниром'' в графе называется вершина, удаление которой увеличивает число компонент связности.
| |
| − | | |
| − | Связный граф называется ''вершинно-<math>k</math>-связным'' (или просто <math>k</math>-связным), если он имеет более <math>k</math> вершин и после удаления любых <math>k-1</math> из них остаётся связным. Максимальное такое число <math>k</math> называется ''вершинной связностью'' (или просто ''связностью'') графа. 1-связный граф называется связным, 2-связный граф – двусвязным.
| |
| − | | |
| − | Связный граф называется ''рёберно-<math>k</math>-связным'', если он остаётся связным после удаления любых <math>k-1</math> рёбер. Максимальное такое число <math>k</math> называется ''рёберной связностью'' графа.
| |
| − | | |
| − | ''Компонентой двусвязности'' графа называется максимальный по включению двусвязный подграф.
| |
| − | | |
| − | == Свойства ==
| |
| | | | |
| − | Эквивалентные определения компоненты связности:
| + | '''Вторая''' группа вершин расположена в двумерной области, соответствующая ей операция <math>a / b</math>. |
| − | * все вершины, достижимые из какой-либо выбранной вершины; | + | Естественно введённые координаты области таковы: |
| − | * набор вершин, достижимых друг из друга, и не достижимых из других вершин. | + | * <math>i</math> — меняется в диапазоне от <math>1</math> до <math>n-1</math>, принимая все целочисленные значения; |
| | + | * <math>j</math> — меняется в диапазоне от <math>i+1</math> до <math>n</math>, принимая все целочисленные значения. |
| | | | |
| − | Отношение «вершина <math>v</math> достижима из вершины <math>u</math>» является отношением эквивалентности. Таким образом, поиск связных компонент графа это то же самое, что восстановление полного отношения эквивалентности по его части.
| + | Аргументы операции следующие: |
| | + | *<math>a</math>: |
| | + | ** при <math>i = 1</math> — элементы ''входных данных'', а именно <math>a_{j1}</math>; |
| | + | ** при <math>i > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i - 1, j, i - 1</math>; |
| | + | * <math>b</math> — результат срабатывания операции, соответствующей вершине из первой группы, с координатой <math>i</math>. |
| | | | |
| − | Альтернативные определения моста:
| + | Результат срабатывания операции является ''выходным данным'' <math>l_{ji}</math>. |
| − | * ребро является мостом, если не участвует ни в одном цикле;
| |
| − | * ребро <math>e</math> является мостом, если существует пара вершин <math>(u, v)</math> из одной компоненты связности, любой путь <math>P(u, v)</math> между которыми проходит через ребро <math>e</math>.
| |
| | | | |
| − | Шарнир разделяет компоненты двусвязности (если две компоненты двусвязности имеют общую вершину, то это шарнир).
| + | '''Третья''' группа вершин расположена в трёхмерной области, соответствующая ей операция <math>a - b * c</math>. |
| | + | Естественно введённые координаты области таковы: |
| | + | * <math>i</math> — меняется в диапазоне от <math>2</math> до <math>n</math>, принимая все целочисленные значения; |
| | + | * <math>j</math> — меняется в диапазоне от <math>i</math> до <math>n</math>, принимая все целочисленные значения; |
| | + | * <math>p</math> — меняется в диапазоне от <math>1</math> до <math>i - 1</math>, принимая все целочисленные значения. |
| | | | |
| − | Каждая из вершин моста является шарниром (кроме случая, когда мост является единственным ребром этой вершины).
| + | Аргументы операции следующие: |
| | + | *<math>a</math>: |
| | + | ** при <math>p = 1</math> элемент входных данных <math>a_{ji}</math>; |
| | + | ** при <math>p > 1</math> — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами <math>i, j, p - 1</math>; |
| | + | *<math>b</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, i</math>; |
| | + | *<math>c</math> — результат срабатывания операции, соответствующей вершине из второй группы, с координатами <math>p, j</math>; |
| | | | |
| − | Компонента сильной связности является объединением всех циклом, проходящих через её вершины.
| + | Результат срабатывания операции является ''промежуточным данным'' алгоритма. |
| | | | |
| − | == Алгоритмы == | + | Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая <math>n = 4</math>. Здесь вершины первой группы обозначены жёлтым цветом и буквосочетанием sq, вершины второй — зелёным цветом и знаком деления, третьей — красным цветом и буквой f. Вершины, соответствующие операциям, производящим выходные данные алгоритма, выполнены более крупно. Дублирующие друг друга дуги даны как одна. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным. |
| | | | |
| − | Компоненты связности могут быть найдены:
| + | [[file:Cholesky full.png|thumb|center|1400px|Рисунок 1. Граф алгоритма без отображения входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление.]] |
| − | * последовательным применением алгоритма [[Поиск в ширину (BFS)|поиска в ширину]] за время <math>O(m)</math>;
| + | [[file:Cholesky full_in_out.png|thumb|center|1400px|Рисунок 2. Граф алгоритма с отображением входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.]] |
| − | * с помощью [[Система непересекающихся множеств|системы непересекающихся множеств]]<ref>Tarjan, Robert Endre. “Efficiency of a Good but Not Linear Set Union Algorithm.” Journal of the ACM 22, no. 2 (April 1975): 215–25. doi:10.1145/321879.321884.</ref> за время <math>O(m \alpha(m, n))</math>, с возможностью эффективной многопоточной реализации<ref>Anderson, Richard J, and Heather Woll. “Wait-Free Parallel Algorithms for the Union-Find Problem,” 370–80, New York, New York, USA: ACM Press, 1991. doi:10.1145/103418.103458.</ref>;
| |
| − | * параллельным алгоритмом [[Алгоритм Шилоаха-Вишкина поиска компонент связности|Шилоаха-Вишкина]]<ref>Shiloach, Yossi, and Uzi Vishkin. “An <math>O(\log n)</math> Parallel Connectivity Algorithm.” Journal of Algorithms 3, no. 1 (March 1982): 57–67. doi:10.1016/0196-6774(82)90008-6.</ref> за время <math>O(\ln n)</math> на <math>n + 2m</math> процессорах.
| |
| | | | |
| − | Компоненты сильной связности могут быть найдены:
| + | === Ресурс параллелизма алгоритма === |
| − | * [[Алгоритм Тарьяна поиска компонент сильной связности|алгоритмом Тарьяна]]<ref name=DFS>Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.</ref> (в ходе [[Поиск в глубину (DFS)|поиска в глубину]]) за время <math>O(m)</math>;
| |
| − | * [[Алгоритм DCSC поиска компонент сильной связности|параллельным алгоритмом DCSC]]<ref>Fleischer, Lisa K, Bruce Hendrickson, and Ali Pınar. “On Identifying Strongly Connected Components in Parallel.” In Lecture Notes in Computer Science, Volume 1800, Springer, 2000, pp. 505–11. doi:10.1007/3-540-45591-4_68.</ref><ref>McLendon, William, III, Bruce Hendrickson, Steven J Plimpton, and Lawrence Rauchwerger. “Finding Strongly Connected Components in Distributed Graphs.” Journal of Parallel and Distributed Computing 65, no. 8 (August 2005): 901–10. doi:10.1016/j.jpdc.2005.03.007.</ref><ref>Hong, Sungpack, Nicole C Rodia, and Kunle Olukotun. “On Fast Parallel Detection of Strongly Connected Components (SCC) in Small-World Graphs,” Proceeedings of SC'13, 1–11, New York, New York, USA: ACM Press, 2013. doi:10.1145/2503210.2503246.</ref> с работой <math>O(n \ln n)</math>.
| |
| | | | |
| − | Мосты могут быть найдены:
| + | Для разложения матрицы порядка <math>n</math> методом Холецкого в параллельном варианте требуется последовательно выполнить следующие ярусы: |
| − | * [[Алгоритм Тарьяна поиска «мостов» в графе|алгоритмом Тарьяна]]<ref>Tarjan, R Endre. “A Note on Finding the Bridges of a Graph.” Information Processing Letters 2, no. 6 (April 1974): 160–61. doi:10.1016/0020-0190(74)90003-9.</ref> (в ходе [[Поиск в глубину (DFS)|поиска в глубину]]) за время <math>O(m)</math>;
| + | * <math>n</math> ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов), |
| − | * параллельным [[Алгоритм Тарьяна-Вишкина поиска компонент двусвязности|алгоритмом Тарьяна-Вишкина]]<ref>Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.</ref> за время <math>O(\ln n)</math> на <math>O(m + n)</math> процессорах; | + | * <math>n - 1</math> ярус делений (в каждом из ярусов линейное количество делений, в зависимости от яруса — от <math>1</math> до <math>n - 1</math>), |
| − | * онлайн-алгоритмом Уэстбрука-Тарьяна<ref name=WestbrookTarjan>Westbrook, Jeffery, and Robert Endre Tarjan. “Maintaining Bridge-Connected and Biconnected Components on-Line.” Algorithmica 7, no. 1 (June 1992): 433–64. doi:10.1007/BF01758773.</ref> за время <math>O(m \alpha(m, n))</math>. | + | * по <math>n - 1</math> ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от <math>1</math> до <math>\frac{n^2 - n}{2}</math>. |
| − | | |
| − | Компоненты двусвязности могут быть найдены:
| |
| − | * [[Алгоритм Тарьяна поиска компонент двусвязности|алгоритмом Тарьяна]]<ref name=DFS /> (в ходе [[Поиск в глубину (DFS)|поиска в глубину]]) за время <math>O(m)</math> (алгоритм также находит и соответствующие шарниры);
| |
| − | * параллельным [[Алгоритм Тарьяна-Вишкина поиска компонент двусвязности|алгоритмом Тарьяна-Вишкина]]<ref>Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.</ref> за время <math>O(\ln n)</math> на <math>O(m + n)</math> процессорах (алгоритм также может находить и мосты); | |
| − | * онлайн-алгоритмом Уэстбрука-Тарьяна<ref name=WestbrookTarjan /> за время <math>O(m \alpha(m, n))</math>.
| |
| | | | |
| − | Задача [[Определение вершинной связности графа|определения вершинной связности графа]] сводится к [[Поиск максимального потока в нагруженном графе|поиску максимальных потоков]] и может быть решена за время <math>O(\min\{k^3 + n, kn\} m)</math><ref>Henzinger, Monika R, Satish Rao, and Harold N Gabow. “Computing Vertex Connectivity: New Bounds From Old Techniques.” Journal of Algorithms 34, no. 2 (February 2000): 222–50. doi:10.1006/jagm.1999.1055.</ref>.
| + | Таким образом, в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах [[глоссарий#Ярусно-параллельная форма графа алгоритма|ЯПФ]] отдельных вычислений квадратных корней может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (деления и тем более умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени. Таким образом, общая экономия в 2 раза, из-за которой метод Холецкого предпочитают в случае симметричных задач тому же методу Гаусса, в параллельном случае уже имеет место вовсе не по всем ресурсам, и главное - не по требуемому времени. |
| | | | |
| − | Рёберная связность графа может быть найдена [[Алгоритм Габова определения рёберной связности графа|алгоритмом Габова]]<ref>Gabow, H N. “A Matroid Approach to Finding Edge Connectivity and Packing Arborescences.” Journal of Computer and System Sciences 50, no. 2 (April 1995): 259–73. doi:10.1006/jcss.1995.1022.</ref> за время <math>O(k m \ln (n^2/m))</math> для ориентированного и <math>O(m + k^2 n \ln (n/k))</math> неориентированного графа. Проверка свойства <math>k</math>-связности тем же алгоритмом может быть выполнена за время <math>O(m + n \ln n)</math>.
| + | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения метода Холецкого в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает увеличение требуемой памяти почти в 2 раза. |
| | | | |
| − | = Поиск максимального потока в транспортной сети =
| + | При классификации по высоте ЯПФ, таким образом, метод Холецкого относится к алгоритмам со сложностью <math>O(n)</math>. При классификации по ширине ЯПФ его сложность будет <math>O(n^2)</math>. |
| | | | |
| − | == Постановка задачи == | + | === Входные и выходные данные алгоритма === |
| | | | |
| − | ''Транспортной сетью'' называется ориентированный граф <math>G = (V, E)</math>, каждому ребру <math>e \in E</math> которого приписана неотрицательная пропускная способность <math>c(e) \ge 0</math>. Будем считать, что вместе с каждым ребром <math>e = (v, w) \in E</math> граф содержит и обратное к нему <math>e^R = (w, v)</math> (при необходимости приписывая ему нулевую пропускную способность). | + | '''Входные данные''': плотная матрица <math>A</math> (элементы <math>a_{ij}</math>). |
| | + | Дополнительные ограничения: |
| | + | * <math>A</math> – симметрическая матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>. |
| | + | * <math>A</math> – положительно определённая матрица, т. е. для любых ненулевых векторов <math>\vec{x}</math> выполняется <math>\vec{x}^T A \vec{x} > 0</math>. |
| | | | |
| − | Пусть в графе <math>G</math> выделены две вершины: источник <math>s</math> и сток <math>t</math>. Без ограничения общности можно считать, что все остальные вершины лежат на каком-либо пути из <math>s</math> в <math>t</math>. ''Потоком'' называется функция <math>f: E \to \mathbb{R}</math>, удовлетворяющая следующим требованиям:
| + | '''Объём входных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в библиотеке, реализованной в НИВЦ МГУ, матрица A хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своего нижнего треугольника. |
| − | * ограничение по пропускной способности: <math>f(e) \le c(e)</math>;
| |
| − | * антисимметричность: <math>f(e^R) = -f(e)</math>;
| |
| − | * закон сохранения потока:
| |
| | | | |
| − | :<math> | + | '''Выходные данные''': нижняя треугольная матрица <math>L</math> (элементы <math>l_{ij}</math>). |
| − | \forall v \ne s, t: \quad \sum_{e = (w, v)} f(e) = \sum_{e = (v, w)} f(e).
| |
| − | </math> | |
| | | | |
| − | ''Величиной потока'' называется суммарный поток из источника: | + | '''Объём выходных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу треугольности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в той же библиотеке, созданной в НИВЦ МГУ, матрица <math>L</math> хранилась в одномерном массиве длины <math>\frac{n (n + 1)}{2}</math> по строкам своей нижней части. |
| | | | |
| − | :<math>
| + | === Свойства алгоритма === |
| − | \lvert f \rvert = \sum_{e = (s, v)} f(e).
| |
| − | </math>
| |
| − | | |
| − | '''Задача о максимальном потоке в транспортной сети.''' Требуется найти поток максимальной величины:
| |
| − | :<math>\lvert f \rvert \to \max.</math>
| |
| | | | |
| − | == Свойства задачи ==
| + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является ''квадратичным'' (отношение кубической к линейной). |
| | | | |
| − | Суммарный поток из источника равен суммарному потоку в сток:
| + | При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь ''линейна''. |
| − | :<math>
| |
| − | \forall v \ne s, t: \quad \sum_{e = (s, v)} f(e) = \sum_{e = (v, t)} f(e).
| |
| − | </math>
| |
| − | (Для доказательства достаточно просуммировать закон сохранения потока для всех вершин, кроме источника и стока.)
| |
| | | | |
| − | == Варианты задачи ==
| + | При этом алгоритм почти полностью детерминирован, это гарантируется теоремой о единственности разложения. Использование другого порядка выполнения ассоциативных операций может привести к накоплению ошибок округления, однако это влияние в используемых вариантах алгоритма не так велико, как, скажем, отказ от использования режима накопления. |
| | | | |
| − | В зависимости от ограничений на значения пропускной способности:
| + | Дуги информационного графа, исходящие из вершин, соответствующих операциям квадратного корня и деления, образуют пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы и координат этих вершин). При этом естественно наличие в этих пучках «длинных» дуг. Остальные дуги локальны. |
| − | * произвольная положительная пропускная способность;
| |
| − | * целая пропускная способность;
| |
| − | * единичная пропускная способность (в этом случае максимальный поток равен [[Связность в графах|рёберной связности]] графа).
| |
| | | | |
| − | == Алгоритмы решения задачи ==
| + | Наиболее известной является компактная укладка графа — его проекция на треугольник матрицы, который перевычисляется укладываемыми операциями. При этом «длинные» дуги можно убрать, заменив более дальнюю пересылку комбинацией нескольких ближних (к соседям). |
| | | | |
| − | * [[Алгоритм Форда-Фалкерсона]]<ref>Ford, L R, Jr., and D R Fulkerson. “Maximal Flow Through a Network.” Canadian Journal of Mathematics 8 (1956): 399–404. doi:10.4153/CJM-1956-045-5.</ref> и его варианты<ref>Edmonds, Jack, and Richard M Karp. “Theoretical Improvements in Algorithmic Efficiency for Network Flow Problems.” Journal of the ACM 19, no. 2 (April 1972): 248–64. doi:10.1145/321694.321699.</ref><ref>Диниц, Е. А. “Алгоритм решения задачи о максимальном потоке в сети со степенной оценкой.” Доклады АН СССР 194, no. 4 (1970): 754–57.</ref> со сложностью <math>O(n^2m)</math> (для алгоритма Диница). В случае целых пропускных способностей, не превосходящих <math>K</math>, сложность <math>O(Km)</math>.
| + | [[Глоссарий#Эквивалентное возмущение|Эквивалентное возмущение]] <math>M</math> у метода Холецкого всего вдвое больше, чем возмущение <math>\delta A</math>, вносимое в матрицу при вводе чисел в компьютер: |
| − | * [[Алгоритм проталкивания предпотока]]<ref>Goldberg, Andrew V, and Robert Endre Tarjan. “A New Approach to the Maximum-Flow Problem.” Journal of the ACM 35, no. 4 (October 1988): 921–40. doi:10.1145/48014.61051.</ref> со сложностью <math>O(mn \ln n)</math> (при использовании динамических деревьев Тарьяна-Слитора<ref>Sleator, Daniel D, and Robert Endre Tarjan. “A Data Structure for Dynamic Trees,” STOC'81, 114–22, New York, USA: ACM Press, 1981. doi:10.1145/800076.802464.</ref><ref>Sleator, Daniel Dominic, and Robert Endre Tarjan. “Self-Adjusting Binary Search Trees.” Journal of the ACM 32, no. 3 (July 1985): 652–86. doi:10.1145/3828.3835.</ref>).
| + | <math> |
| − | | + | ||M||_{E} \leq 2||\delta A||_{E} |
| − | Обозначения: <math>m</math> – число рёбер, <math>n</math> – число вершин.
| |
| − | | |
| − | = Задача о назначениях =
| |
| − | | |
| − | == Постановка задачи ==
| |
| − | | |
| − | Пусть имеется <math>n</math> агентов и <math>m</math> задач, которые могут быть распределены между этими агентами. Каждому агенту может быть выделена только одна задача, и каждая задача может быть выделена только одному агенту. Стоимость присвоения <math>i</math>-й задачи <math>j</math>-му агенту равна <math>c(i, j)</math>. В случае <math>c(i, j) = \infty</math> задача <math>j</math> не может быть назначена агенту <math>i</math>.
| |
| − | | |
| − | '''Задача о назначениях''': сформировать допустимое множество назначений <math>A = \{ (i_1, j_1), \ldots, (i_k, j_k) \}</math>, <math>k = \min \{m, n\}</math>, имеющее макисмальную суммарную стоимость:
| |
| − | | |
| − | :<math>
| |
| − | C(A) = \sum_{s = 1}^k c(i_s, j_s) \to \max.
| |
| | </math> | | </math> |
| | | | |
| − | == Варианты задачи ==
| + | Это явление обусловлено положительной определённостью матрицы. Среди всех используемых разложений матриц это наименьшее из эквивалентных возмущений. |
| − | | |
| − | При <math>m = n</math> задача называется ''линейной'': каждому агенту достаётся ровно одна задача, и каждая задача достаётся ровно одному агенту.
| |
| − | | |
| − | В случае единичных весов возникает задача о наибольшем паросочетании в двудольном графе: назначить как можно больше задач.
| |
| | | | |
| − | == Алгоритмы решения задачи == | + | == Литература == |
| | | | |
| − | * [[Венгерский алгоритм]]<ref>Kuhn, H W. “The Hungarian Method for the Assignment Problem.” Naval Research Logistics Quarterly 2, no. 1 (March 1955): 83–97. doi:10.1002/nav.3800020109.</ref><ref>Kuhn, H W. “Variants of the Hungarian Method for Assignment Problems.” Naval Research Logistics Quarterly 3, no. 4 (December 1956): 253–58. doi:10.1002/nav.3800030404.</ref><ref>Munkres, James. “Algorithms for the Assignment and Transportation Problems.” Journal of the Society for Industrial and Applied Mathematics 5, no. 1 (March 1957): 32–38. doi:10.1137/0105003.</ref> для линейной задачи, сложность <math>O(n^4)</math> (может быть уменьшена<ref>Tomizawa, N. “On Some Techniques Useful for Solution of Transportation Network Problems.” Networks 1, no. 2 (1971): 173–94. doi:10.1002/net.3230010206.</ref> до <math>O(n^3)</math>);
| + | <references \> |
| − | * [[Алгоритм аукциона]]<ref>Bertsekas, Dimitri P. “Auction Algorithms for Network Flow Problems: a Tutorial Introduction.” Computational Optimization and Applications 1 (1992): 7–66.</ref><ref>Zavlanos, Michael M, Leonid Spesivtsev, and George J Pappas. “A Distributed Auction Algorithm for the Assignment Problem,” Proceedings of IEEE CDC'08, 1212–17, IEEE, 2008. doi:10.1109/CDC.2008.4739098.</ref>;
| |
| − | * [[Алгоритм Гопкрофта-Карпа]]<ref>Hopcroft, John E, and Richard M Karp. “An $N^{5/2} $ Algorithm for Maximum Matchings in Bipartite Graphs.” SIAM Journal on Computing 2, no. 4 (1973): 225–31. doi:10.1137/0202019.</ref> для задачи с единичными ценами, сложность <math>O(m \sqrt{n})</math>.
| |
| Разложение Холецкого
|
| Последовательный алгоритм
|
| Последовательная сложность
|
[math]O(n^3)[/math]
|
| Объём входных данных
|
[math]\frac{n (n + 1)}{2}[/math]
|
| Объём выходных данных
|
[math]\frac{n (n + 1)}{2}[/math]
|
| Параллельный алгоритм
|
| Высота ярусно-параллельной формы
|
[math]O(n)[/math]
|
| Ширина ярусно-параллельной формы
|
[math]O(n^2)[/math]
|
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Разложение Холецкого впервые предложено французским офицером и математиком Андре-Луи Холецким в конце Первой Мировой войны, незадолго до его гибели в бою в августе 1918 г. Идея этого разложения была опубликована в 1924 г. его сослуживцем[1]. Потом оно было использовано поляком Т. Банашевичем[2][3] в 1938 г. В советской математической литературе называется также методом квадратного корня[4][5][6]; название связано с характерными операциями, отсутствующими в родственном разложении Гаусса.
Первоначально разложение Холецкого использовалось исключительно для плотных симметричных положительно определенных матриц. В настоящее время его использование гораздо шире. Оно может быть применено также, например, к эрмитовым матрицам. Для повышения производительности вычислений часто применяется блочная версия разложения.
Для разреженных матриц разложение Холецкого также широко применяется в качестве основного этапа прямого метода решения линейных систем. В этом случае используют специальные упорядочивания для уменьшения ширины профиля исключения, а следовательно и уменьшения количества арифметических операций. Другие упорядочивания используются для выделения независимых блоков вычислений при работе на системах с параллельной организацией.
Варианты разложения Холецкого нашли успешные применения и в итерационных методах для построения переобусловливателей разреженных симметричных положительно определенных матриц. В неполном треугольном разложении («по позициям») элементы переобусловливателя вычисляются только в заранее заданных позициях, например, в позициях ненулевых элементов исходной матрицы (так называемое разложение IC0). Для получения же более точного разложения применяется приближение, в котором фильтрация малых элементов производится «по значениям». В зависимости от используемого порога фильтрации можно получить более точное, но и более заполненное разложение. Существует и алгоритм разложения второго порядка точности[7]. В нём при таком же заполнении множителей разложения удается улучшить точность. Для такого разложения в параллельном режиме используется специальный вариант аддитивного переобуславливания на основе разложения второго порядка[8].
На этой странице представлено исходное разложение Холецкого с новых позиций нашего суперкомпьютерного века. Приведено описание конкретной версии разложения Холецкого — для плотных вещественных симметричных положительно определённых матриц, но структура для ряда других версий, например, для комплексного случая, почти такая же, различия состоят в замене большинства вещественных операций на комплексные. Список остальных основных вариантов разложения можно посмотреть на странице Метод Холецкого (нахождение симметричного треугольного разложения).
Используется для разложения положительно определённых эрмитовых (в вещественном случае - симметрических) матриц в виде [math]A = L L^*[/math] ([math]L[/math] — нижняя треугольная матрица) или в виде [math]A = U^* U[/math] ([math]U[/math] — верхняя треугольная матрица ; эти разложения совершенно эквивалентны друг другу по вычислениям и различаются только способом представления данных). Он заключается в реализации формул для элементов матрицы [math]L[/math], получающихся из вышеприведённого равенства единственным образом. Получило широкое распространение благодаря следующим особенностям.
1.1.1 Симметричность и положительная определённость матрицы
Симметричность матрицы позволяет хранить и вычислять только чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций в сравнении с, например, разложением по методу Гаусса. При этом альтернативное (без вычисления квадратных корней) LU-разложение, использующее симметрию матрицы, всё же несколько быстрее метода Холецкого (не использует извлечение квадратных корней), но требует хранения всей матрицы.
Благодаря тому, что разлагаемая матрица не только симметрична, но и положительно определена, её LU-разложения, в том числе и разложение методом Холецкого, имеют наименьшее эквивалентное возмущение из всех известных разложений матриц.
1.1.2 Режим накопления
Алгоритм позволяет использовать так называемый режим накопления, обусловленный тем, что значительную часть вычислений составляют вычисления скалярных произведений.
1.2 Математическое описание алгоритма
Исходные данные: положительно определённая симметрическая матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Вычисляемые данные: нижняя треугольная матрица [math]L[/math] (элементы [math]l_{ij}[/math]).
Формулы метода:
- [math]
\begin{align}
l_{11} & = \sqrt{a_{11}}, \\
l_{j1} & = \frac{a_{j1}}{l_{11}}, \quad j \in [2, n], \\
l_{ii} & = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}, \quad i \in [2, n], \\
l_{ji} & = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}, \quad i \in [2, n - 1], j \in [i + 1, n].
\end{align}
[/math]
Существует также блочная версия метода, однако в данном описании разобран только точечный метод.
В ряде реализаций деление на диагональный элемент выполняется в два этапа: вычисление [math]\frac{1}{l_{ii}}[/math] и затем умножение на него всех (видоизменённых) [math]a_{ji}[/math] . Здесь мы этот вариант алгоритма не рассматриваем. Заметим только, что он имеет худшие параллельные характеристики, чем представленный.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательной версии метода Холецкого можно составить из множественных (всего их [math]\frac{n (n - 1)}{2}[/math]) вычислений скалярных произведений строк матрицы:
- [math]\sum_{p = 1}^{i - 1} l_{ip} l_{jp}[/math]
в режиме накопления или без него, в зависимости от требований задачи. Во многих последовательных реализациях упомянутый способ представления не используется. Дело в том, что в них вычисление сумм типа
- [math]a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}[/math]
в которых и встречаются скалярные произведения, ведутся не в порядке «вычислили скалярное произведение, а потом вычли его из элемента», а путём вычитания из элемента покомпонентных произведений, являющихся частями скалярных произведений. Поэтому следует считать вычислительным ядром метода не вычисления скалярных произведений, а вычисления выражений
- [math]a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}[/math]
в режиме накопления или без него.
Тем не менее, в популярных зарубежных реализациях точечного метода Холецкого, в частности, в библиотеках LINPACK и LAPACK, основанных на BLAS, используются именно вычисления скалярных произведений в виде вызова соответствующих подпрограмм BLAS (конкретно — функции SDOT). На последовательном уровне это влечёт за собой дополнительную операцию суммирования на каждый из [math]\frac{n (n + 1)}{2}[/math] вычисляемый элемент матрицы [math]L[/math] и некоторое замедление работы программы (о других следствиях рассказано ниже в разделе «Существующие реализации алгоритма»). Поэтому в данных вариантах ядром метода Холецкого будут вычисления этих скалярных произведений.
1.4 Макроструктура алгоритма
Как записано и в описании ядра алгоритма, основную часть метода составляют множественные (всего [math]\frac{n (n - 1)}{2}[/math]) вычисления сумм
- [math]a_{ji}-\sum_{p=1}^{i-1}l_{ip} l_{jp}[/math]
в режиме накопления или без него.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. [math]l_{11}= \sqrt{a_{11}}[/math]
2. [math]l_{j1}= \frac{a_{j1}}{l_{11}}[/math] (при [math]j[/math] от [math]2[/math] до [math]n[/math]).
Далее для всех [math]i[/math] от [math]2[/math] до [math]n[/math] по нарастанию выполняются
3. [math]l_{ii} = \sqrt{a_{ii} - \sum_{p = 1}^{i - 1} l_{ip}^2}[/math] и
4. (кроме [math]i = n[/math]): [math]l_{ji} = \left (a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp} \right ) / l_{ii}[/math] (для всех [math]j[/math] от [math]i + 1[/math] до [math]n[/math]).
После этого (если [math]i \lt n[/math]) происходит переход к шагу 3 с бо́льшим [math]i[/math].
Особо отметим, что вычисления сумм вида [math]a_{ji} - \sum_{p = 1}^{i - 1} l_{ip} l_{jp}[/math] в обеих формулах производят в режиме накопления вычитанием из [math]a_{ji}[/math] произведений [math]l_{ip} l_{jp}[/math] для [math]p[/math] от [math]1[/math] до [math]i - 1[/math], c нарастанием [math]p[/math].
1.6 Последовательная сложность алгоритма
Для разложения матрицы порядка n методом Холецкого в последовательном (наиболее быстром) варианте требуется:
- [math]n[/math] вычислений квадратного корня,
- [math]\frac{n(n-1)}{2}[/math] делений,
- [math]\frac{n^3-n}{6}[/math] сложений (вычитаний),
- [math]\frac{n^3-n}{6}[/math] умножений.
Умножения и сложения (вычитания) составляют основную часть алгоритма.
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает долю умножений и сложений/вычитаний во времени, требуемом для выполнения метода Холецкого.
При классификации по последовательной сложности, таким образом, метод Холецкого относится к алгоритмам с кубической сложностью.
1.7 Информационный граф
Опишем граф алгоритма[9][10][11] как аналитически, так и в виде рисунка.
Граф алгоритма состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.
Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT.
Единственная координата каждой из вершин [math]i[/math] меняется в диапазоне от [math]1[/math] до [math]n[/math], принимая все целочисленные значения.
Аргумент этой функции
- при [math]i = 1[/math] — элемент входных данных, а именно [math]a_{11}[/math];
- при [math]i \gt 1[/math] — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами [math]i - 1[/math], [math]i[/math], [math]i - 1[/math].
Результат срабатывания операции является выходным данным [math]l_{ii}[/math].
Вторая группа вершин расположена в двумерной области, соответствующая ей операция [math]a / b[/math].
Естественно введённые координаты области таковы:
- [math]i[/math] — меняется в диапазоне от [math]1[/math] до [math]n-1[/math], принимая все целочисленные значения;
- [math]j[/math] — меняется в диапазоне от [math]i+1[/math] до [math]n[/math], принимая все целочисленные значения.
Аргументы операции следующие:
- [math]a[/math]:
- при [math]i = 1[/math] — элементы входных данных, а именно [math]a_{j1}[/math];
- при [math]i \gt 1[/math] — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами [math]i - 1, j, i - 1[/math];
- [math]b[/math] — результат срабатывания операции, соответствующей вершине из первой группы, с координатой [math]i[/math].
Результат срабатывания операции является выходным данным [math]l_{ji}[/math].
Третья группа вершин расположена в трёхмерной области, соответствующая ей операция [math]a - b * c[/math].
Естественно введённые координаты области таковы:
- [math]i[/math] — меняется в диапазоне от [math]2[/math] до [math]n[/math], принимая все целочисленные значения;
- [math]j[/math] — меняется в диапазоне от [math]i[/math] до [math]n[/math], принимая все целочисленные значения;
- [math]p[/math] — меняется в диапазоне от [math]1[/math] до [math]i - 1[/math], принимая все целочисленные значения.
Аргументы операции следующие:
- [math]a[/math]:
- при [math]p = 1[/math] элемент входных данных [math]a_{ji}[/math];
- при [math]p \gt 1[/math] — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами [math]i, j, p - 1[/math];
- [math]b[/math] — результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math]p, i[/math];
- [math]c[/math] — результат срабатывания операции, соответствующей вершине из второй группы, с координатами [math]p, j[/math];
Результат срабатывания операции является промежуточным данным алгоритма.
Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая [math]n = 4[/math]. Здесь вершины первой группы обозначены жёлтым цветом и буквосочетанием sq, вершины второй — зелёным цветом и знаком деления, третьей — красным цветом и буквой f. Вершины, соответствующие операциям, производящим выходные данные алгоритма, выполнены более крупно. Дублирующие друг друга дуги даны как одна. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным.
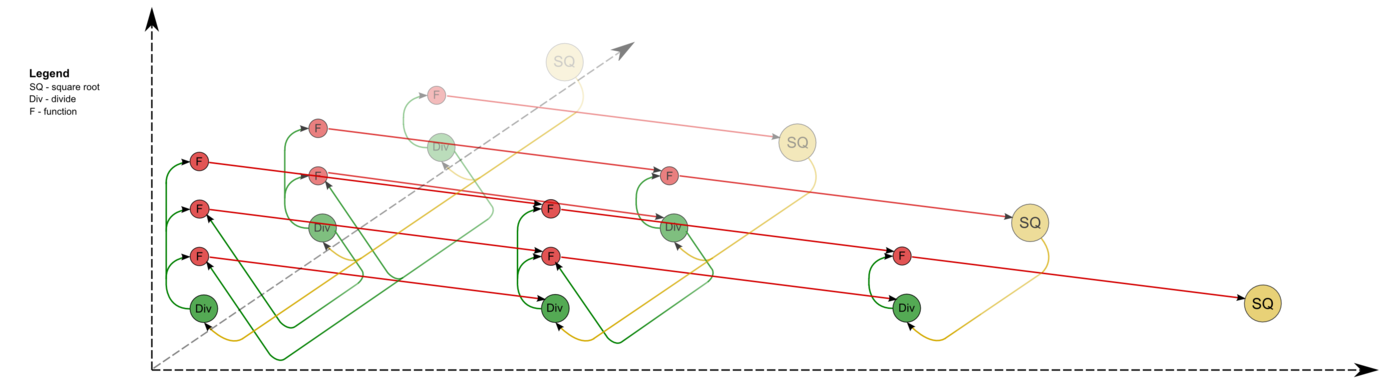
Рисунок 1. Граф алгоритма без отображения входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление.
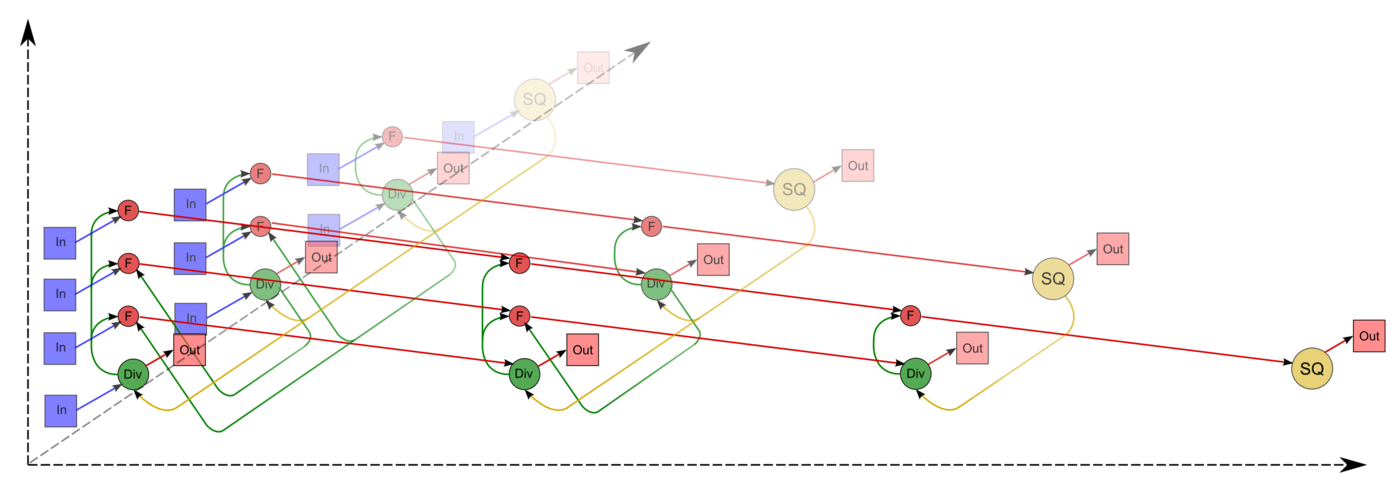
Рисунок 2. Граф алгоритма с отображением входных и выходных данных. SQ - вычисление квадратного корня, F - операция a-bc, Div - деление, In - входные данные, Out - результаты.
1.8 Ресурс параллелизма алгоритма
Для разложения матрицы порядка [math]n[/math] методом Холецкого в параллельном варианте требуется последовательно выполнить следующие ярусы:
- [math]n[/math] ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов),
- [math]n - 1[/math] ярус делений (в каждом из ярусов линейное количество делений, в зависимости от яруса — от [math]1[/math] до [math]n - 1[/math]),
- по [math]n - 1[/math] ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от [math]1[/math] до [math]\frac{n^2 - n}{2}[/math].
Таким образом, в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и делений будут определять довольно значительную долю требуемого времени. При реализации на конкретных архитектурах наличие в отдельных ярусах ЯПФ отдельных вычислений квадратных корней может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (деления и тем более умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени. Таким образом, общая экономия в 2 раза, из-за которой метод Холецкого предпочитают в случае симметричных задач тому же методу Гаусса, в параллельном случае уже имеет место вовсе не по всем ресурсам, и главное - не по требуемому времени.
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения метода Холецкого в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает увеличение требуемой памяти почти в 2 раза.
При классификации по высоте ЯПФ, таким образом, метод Холецкого относится к алгоритмам со сложностью [math]O(n)[/math]. При классификации по ширине ЯПФ его сложность будет [math]O(n^2)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Дополнительные ограничения:
- [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math].
- [math]A[/math] – положительно определённая матрица, т. е. для любых ненулевых векторов [math]\vec{x}[/math] выполняется [math]\vec{x}^T A \vec{x} \gt 0[/math].
Объём входных данных: [math]\frac{n (n + 1)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в библиотеке, реализованной в НИВЦ МГУ, матрица A хранилась в одномерном массиве длины [math]\frac{n (n + 1)}{2}[/math] по строкам своего нижнего треугольника.
Выходные данные: нижняя треугольная матрица [math]L[/math] (элементы [math]l_{ij}[/math]).
Объём выходных данных: [math]\frac{n (n + 1)}{2}[/math] (в силу треугольности достаточно хранить только ненулевые элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. Например, в той же библиотеке, созданной в НИВЦ МГУ, матрица [math]L[/math] хранилась в одномерном массиве длины [math]\frac{n (n + 1)}{2}[/math] по строкам своей нижней части.
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является квадратичным (отношение кубической к линейной).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – всего лишь линейна.
При этом алгоритм почти полностью детерминирован, это гарантируется теоремой о единственности разложения. Использование другого порядка выполнения ассоциативных операций может привести к накоплению ошибок округления, однако это влияние в используемых вариантах алгоритма не так велико, как, скажем, отказ от использования режима накопления.
Дуги информационного графа, исходящие из вершин, соответствующих операциям квадратного корня и деления, образуют пучки т. н. рассылок линейной мощности (то есть степень исхода этих вершин и мощность работы с этими данными — линейная функция от порядка матрицы и координат этих вершин). При этом естественно наличие в этих пучках «длинных» дуг. Остальные дуги локальны.
Наиболее известной является компактная укладка графа — его проекция на треугольник матрицы, который перевычисляется укладываемыми операциями. При этом «длинные» дуги можно убрать, заменив более дальнюю пересылку комбинацией нескольких ближних (к соседям).
Эквивалентное возмущение [math]M[/math] у метода Холецкого всего вдвое больше, чем возмущение [math]\delta A[/math], вносимое в матрицу при вводе чисел в компьютер:
[math]
||M||_{E} \leq 2||\delta A||_{E}
[/math]
Это явление обусловлено положительной определённостью матрицы. Среди всех используемых разложений матриц это наименьшее из эквивалентных возмущений.
2 Литература
<references \>
- ↑ Commandant Benoit, Note sur une méthode de résolution des équations normales provenant de l'application de la méthode des moindres carrés à un système d'équations linéaires en nombre inférieur à celui des inconnues (Procédé du Commandant Cholesky), Bulletin Géodésique 2 (1924), 67-77.
- ↑ Banachiewicz T. Principles d'une nouvelle technique de la méthode des moindres carrês. Bull. Intern. Acad. Polon. Sci. A., 1938, 134-135.
- ↑ Banachiewicz T. Méthode de résoltution numérique des équations linéaires, du calcul des déterminants et des inverses et de réduction des formes quardatiques. Bull. Intern. Acad. Polon. Sci. A., 1938, 393-401.
- ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
- ↑ Воеводин В.В., Кузнецов Ю.А. Матрицы и вычисления. М.: Наука, 1984.
- ↑ Фаддеев Д.К., Фаддева В.Н. Вычислительные основы линейной алгебры. М.-Л.: Физматгиз, 1963.
- ↑ Kaporin I.E. High quality preconditioning of a general symmetric positive definite matrix based on its UTU + UTR + RTU-decomposition. Numer. Lin. Algebra Appl. (1998) Vol. 5, No. 6, 483-509.
- ↑ Капорин И.Е., Коньшин И.Н. Параллельное решение симметричных положительно-определенных систем на основе перекрывающегося разбиения на блоки. Ж. вычисл. матем. и матем. физ., 2001, Т, 41, N. 4, C. 515–528.
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
- ↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
- ↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.

