Поиск в ширину (BFS): различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Elijah (обсуждение | вклад) |
Elijah (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | {{algorithm | ||
| + | | name = Алгоритм DCSC поиска компонент сильной связности | ||
| + | | serial_complexity = <math>O(n + m)</math> | ||
| + | | pf_height = <math>N/A, max O(V) </math> | ||
| + | | pf_width = <math>N/A, max O(E) </math> | ||
| + | | input_data = <math>O(m + n)</math> | ||
| + | | output_data = <math>O(n)</math> | ||
| + | }} | ||
| + | |||
| + | Основные авторы описания: [[Участник:Elijah|И.В.Афанасьев]] | ||
| + | |||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| − | '''Поиск в ширину''' (англ. Breadth-First Search, BFS) позволяет вычислить кратчайшие расстояния (в терминах количества рёбер) от выделенной вершины ориентированного графа до всех остальных вершин, и/или построить корневое направленное дерево, расстояния в котором совпадают с расстояниями в исходном графе. | + | === Общее описание алгоритма === |
| + | |||
| + | '''Поиск в ширину''' (англ. Breadth-First Search, BFS) позволяет вычислить кратчайшие расстояния (в терминах количества рёбер) от выделенной вершины ориентированного графа до всех остальных вершин, и/или построить корневое направленное дерево, расстояния в котором совпадают с расстояниями в исходном графе. Кроме того, поиск в ширину позволяет решать задачу проверки достижимости (существуют ли пути между вершиной источником и остальными вершинами графа). Впервые алгоритм поиска в ширину описан в работах Мура<ref>Moore, Edward F. “The Shortest Path Through a Maze,” International Symposium on the Theory of Switching, 285–92, 1959.</ref> и Ли<ref>Lee, C Y. “An Algorithm for Path Connections and Its Applications.” IEEE Transactions on Electronic Computers 10, no. 3 (September 1961): 346–65. doi:10.1109/TEC.1961.5219222.</ref>. | ||
| + | |||
| + | Алгоритм основан на обходе вершин графа "по слоям". На каждом шаге есть множество "передовых" вершин, для смежных к которым производится проверка, относятся ли они к еще не посещенным. Все еще не посещенные вершины добавляются в новое множество "передовых" вершин, обрабатываемых на следующем шаге. Изначально в множество "передовых" вершин входит только вершина-источник, от которой и начинается обход. | ||
| + | |||
| + | В последовательном случае алгоритм имеет алгоритмическую сложность <math>O(n + m)</math>, где <math>n</math> - число вершин в графе, <math>m</math> - число ребер в графе. | ||
| − | |||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | |||
| + | Пусть задан граф <math>G = (V, E)</math> без весов, и с выделенной вершиной-источником <math>u</math>. Путем <math>P(u,v)</math> между вершинами <math>u</math> и <math>v</math> называется множество ребер <math>(u, v_1), (v_1, v_2), ... (v_n-1, v)</math>. Длиной пути <math>d(u,v)</math> обозначим число ребер в данном пути между вершинами <math>u</math> и <math>v</math>. Поиск в ширину находит кратчайшие пути <math>d(u,v)</math> от вершины <math>u</math> до всех остальных вершин графа следующим образом: | ||
| + | |||
| + | // TODO | ||
| + | |||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| + | |||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
=== Схема реализации последовательного алгоритма === | === Схема реализации последовательного алгоритма === | ||
Версия 21:41, 7 августа 2017
| Алгоритм DCSC поиска компонент сильной связности | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n + m)[/math] |
| Объём входных данных | [math]O(m + n)[/math] |
| Объём выходных данных | [math]O(n)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]N/A, max O(V) [/math] |
| Ширина ярусно-параллельной формы | [math]N/A, max O(E) [/math] |
Основные авторы описания: И.В.Афанасьев
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Поиск в ширину (англ. Breadth-First Search, BFS) позволяет вычислить кратчайшие расстояния (в терминах количества рёбер) от выделенной вершины ориентированного графа до всех остальных вершин, и/или построить корневое направленное дерево, расстояния в котором совпадают с расстояниями в исходном графе. Кроме того, поиск в ширину позволяет решать задачу проверки достижимости (существуют ли пути между вершиной источником и остальными вершинами графа). Впервые алгоритм поиска в ширину описан в работах Мура[1] и Ли[2].
Алгоритм основан на обходе вершин графа "по слоям". На каждом шаге есть множество "передовых" вершин, для смежных к которым производится проверка, относятся ли они к еще не посещенным. Все еще не посещенные вершины добавляются в новое множество "передовых" вершин, обрабатываемых на следующем шаге. Изначально в множество "передовых" вершин входит только вершина-источник, от которой и начинается обход.
В последовательном случае алгоритм имеет алгоритмическую сложность [math]O(n + m)[/math], где [math]n[/math] - число вершин в графе, [math]m[/math] - число ребер в графе.
1.2 Математическое описание алгоритма
Пусть задан граф [math]G = (V, E)[/math] без весов, и с выделенной вершиной-источником [math]u[/math]. Путем [math]P(u,v)[/math] между вершинами [math]u[/math] и [math]v[/math] называется множество ребер [math](u, v_1), (v_1, v_2), ... (v_n-1, v)[/math]. Длиной пути [math]d(u,v)[/math] обозначим число ребер в данном пути между вершинами [math]u[/math] и [math]v[/math]. Поиск в ширину находит кратчайшие пути [math]d(u,v)[/math] от вершины [math]u[/math] до всех остальных вершин графа следующим образом:
// TODO
1.3 Вычислительное ядро алгоритма
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
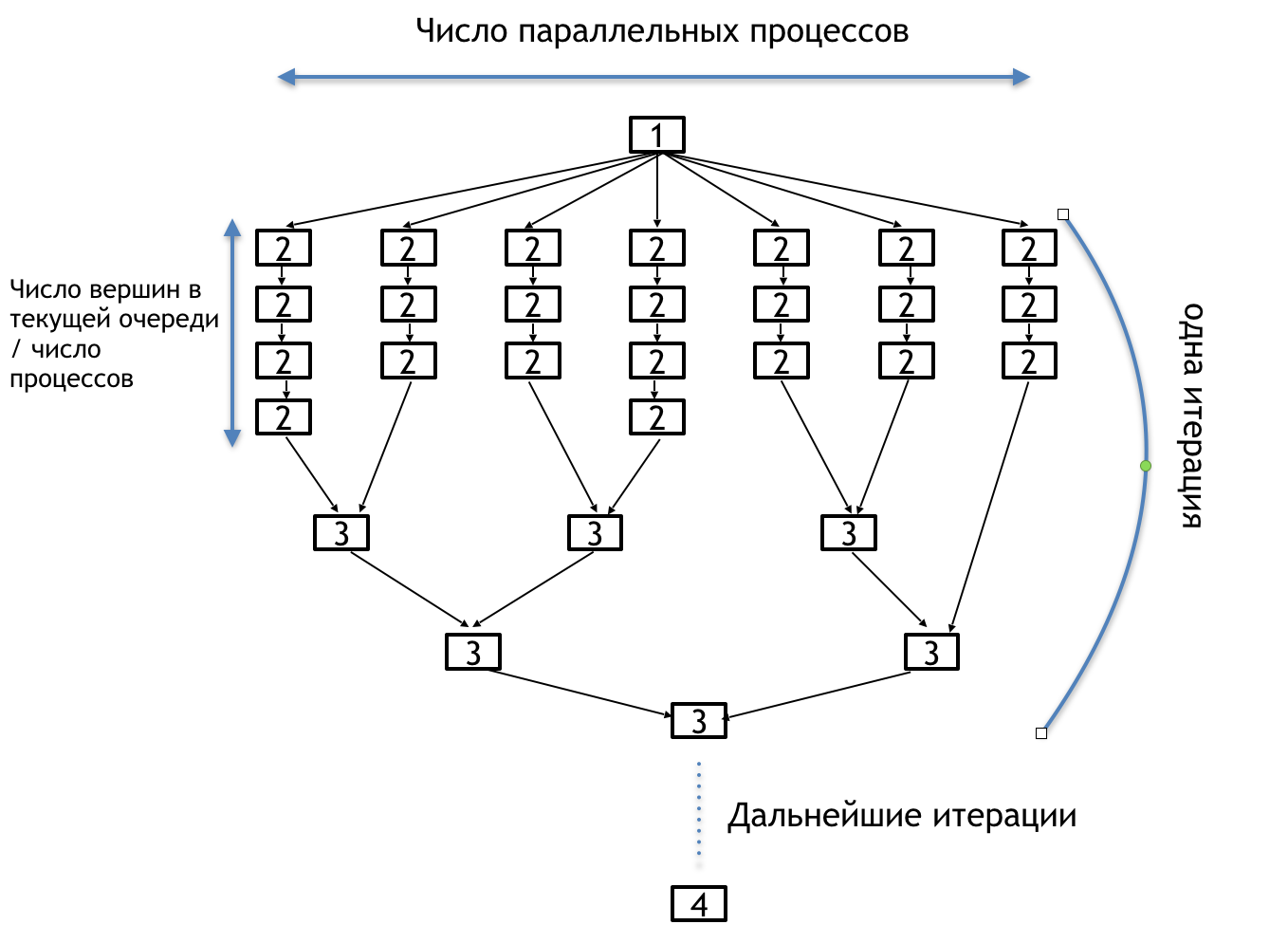
1.7 Информационный граф
Информационный граф
1.8 Ресурс параллелизма алгоритма
1.9 Входные и выходные данные алгоритма
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- Распределённый алгоритм поиска вширь является вычислительным ядром бенчмарка Graph500.
- C++: Boost Graph Library (функции
breadth_first_search,breadth_first_visit). - C++, MPI: Parallel Boost Graph Library (функция
breadth_first_search). - Java: WebGraph (класс
ParallelBreadthFirstVisit), многопоточная реализация. - Python: NetworkX (функция
bfs_edges). - Python/C++: NetworKit (класс
networkit.graph.BFS).