Участник:Адиев Тохтар/Алгоритм кластеризации, основанный на сетях Кохоннена

Алгоритм кластеризации, основанный на сетях Кохонена

Основные авторы описания: Логвиненко Александра 613 и Адиев Тохтар 616

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Рисунок 1. Массив узлов в двумерной SOM сетке.

Cамоорганизующиеся карты Кохонена (Self-Organizing Map (SOM)), представляет собой вычислительный метод, представленный финским ученным Теуво Кохоненом в 1984 году, для визуализации и анализа многомерных данных, прежде всего для экспериментально полученной информации.

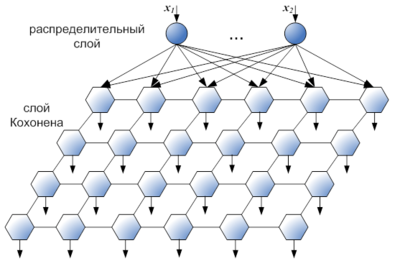
Алгоритм SOM вырос из ранних нейросетевых моделей, особенно моделей ассоциативной памяти и адаптивное обучение (Кохонена 1984). Особый вид нейронных сетей, известных как самоорганизующиеся карты Кохонена, которые используются для решения задач кластеризации данных. Она представляет собой двухслойную сеть. Каждый нейрон первого (распределительного) слоя соединен со всеми нейронами второго (выходного) слоя, которые расположены в виде двумерной решетки. Нейроны выходного слоя называются кластерными элементами, их количество определят максимальное количество групп, на которые система может разделить входные данные. Увеличивая количество нейронов второго слоя можно увеличивать детализацию результатов процесса кластеризации.

Обучение нейронной сети Кохонена относится к типу самообучающегося соревнования. При обучении методом соревнований нейроны соревнуются между собой за право активации.

a)

б)

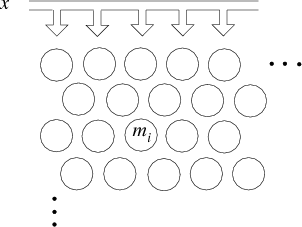
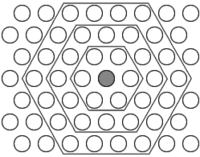
SOM подразумевает использование упорядоченной структуры нейронов. Обычно используются одно и двумерные сетки. При этом каждый нейрон представляет собой [math]n[/math]-мерный вектор-столбец [math] w= [w_1,...,w_n]^T [/math], где [math]n[/math] определяется размерностью исходного пространства (размерностью входных векторов). Применение одно и двумерных сеток связано с тем, что возникают проблемы при отображении пространственных структур большей размерности (при этом опять возникают проблемы с понижением размерности до двумерной, представимой на мониторе). Обычно нейроны располагаются в узлах двумерной сетки с прямоугольными или шестиугольными ячейками. При этом, как было сказано выше, нейроны также взаимодействуют друг с другом. Величина этого взаимодействия определяется расстоянием между нейронами на карте. На рисунках а) и б) дан пример расстояния для шестиугольной и четырехугольной сеток.

Основное отличие сетей Кохонена от других типов нейронных сетей состоит в наглядности и удобстве использования. Эти сети позволяют упростить многомерную структуру, их можно считать одним из методов проецирования многомерного пространства в пространство с более низкой размерностью. Другое принципиальное отличие сетей Кохонена от других моделей нейронных сетей - неуправляемое или неконтролируемое обучение, что позволяет задавать лишь значения входных переменных.

Алгоритм обучения Кохонена и карты Кохонена послужили основой для большого количества исследований в области нейронных сетей, благодаря чему Кохонен считается самым цитируемым финским ученым. Количество научных работ по картам Кохонена составляет около 8 000. Т. Кохонен — автор более 300 публикаций и 4 монографий

Общим недостатком всех рассмотренных алгоритмов обучения нейронной сети Кохонена является наличие в них большого числа эвристических параметров и искусственность предлагаемых решений проблемы «мертвых» нейронов.

Структура алгоритма - двухслойная нейронная сеть.

1.2 Математическое описание алгоритма

Каждый нейрон сети соединен со всеми компонентами n - мерного входного вектора [math] x(t)=[\xi_1(t),\xi_2(t),...,\xi_n(t)][/math] Входной вектор— это описание одного из объектов, подлежащих кластеризации. Количество нейронов совпадает с количеством кластеров, которое должна выделить сеть.

Каждый j-ый нейрон описывается вектором весов [math] w_j(t)=(w_{j1}(t),...,w_{jn}(t))[/math], где n– число компонентов входных векторов.

Обучение сети Кохонена представляет собой подбор значений весов,минимизирующих ошибки от замены близких в смысле используемой метрики входных векторов вектором весов

1.2.1 Алгоритм обучения

шаг 0: Подача исходных данных на входы. Весовой вектор [math]w[/math] выбирается случайным образом. Величины [math] \alpha [/math], [math] h_{kc}[/math] известны.

шаг 1: Выбрать произвольное наблюдение [math] x ( t ) [/math] из множества входных данных.

шаг 2: Определить расстояние между между входным вектором и каждого вектора весовых коэффициентов

[math] d_k(t)=||x(t)-w_k(t)||, k=1,...,n[/math],

шаг 3: Определение нейрона -победителя (веса которого в наименьшей степени отличаются от соответствующих компонентов входного вектора)

[math] d_w(t)=\min\limits_{k}(d_k(t)), k=1,...,n[/math]

шаг 4: Векторы весовых коэффициентов обновляются с помощью функции соседства по формуле

[math] w_k(t+1)=w_k(t)+\alpha(t)h_{kc}(t)||x(t)-w_k(t)||,[/math]

шаг 5: Прекратите, если максимальное число итераций достигнуто; в противном случае изменить параметры [math] \alpha [/math] и [math] h_{kc} [/math] продолжите с шага 1 .

Переменные

• [math]t [/math] -текущая итерация
• [math]\lambda [/math] -предельное значение итераций
• [math]x(t)[/math] -вектор входных данных
• [math]k[/math] -индекс узла в карте
• [math]w_k[/math] -текущий вектор веса в узле k
• [math]c[/math] -индекс нейрона-побдителя
• [math] h_{kc}(t)[/math]- функция "соседства", определяет расстояне между нейроном [math] w_k [/math] и [math] w_c [/math]
• [math]\alpha (t)[/math]- монотонно убывающий коэффициент обучения .

Инициализация начальных весов

Удачно выбранный способ инициализации может существенно ускорить обучение, и привести к получению более качественных результатов. Существуют три способа инициирования начальных весов.

• Инициализация случайными значениями, когда всем весам даются малые случайные величины.

• Инициализация примерами, когда в качестве начальных значений задаются значения случайно выбранных примеров из обучающей выборки.

• Линейная инициализация. В этом случае веса инициируются значениями векторов, линейно упорядоченных вдоль линейного подпространства, проходящего между двумя главных собственными векторами исходного набора данных. Собственные вектора могут быть найдены например при помощи процедуры Грама-Шмидта.

Задание [math]h[/math]

Часто в качестве функции соседства используется гауссовская функция:

[math]h_{ci}(t)=\alpha(t)\cdot\exp(-\frac{\|r_c-r_k\|^2}{2\sigma^2(t)})[/math]

где [math]0\lt \alpha(t)\lt 1[/math] — обучающий сомножитель, монотонно убывающий с каждой последующей итерацией (то есть определяющий приближение значения векторов веса нейрона-победителя и его соседей к наблюдению; чем больше шаг, тем меньше уточнение);
[math]r_k[/math], [math]r_c[/math] — координаты узлов [math]W_k(t)[/math] и [math]W_c(t)[/math] на карте;

[math]\sigma(t)[/math] — сомножитель, уменьшающий количество соседей с итерациями, монотонно убывает. Параметры [math]\alpha[/math], [math]\sigma[/math] и их характер убывания задаются аналитиком.

Более простой способ задания функции соседства:

[math]h_{ck}(t)=\alpha(t)[/math], 

если [math]W_k(t)[/math] находится в окрестности [math]W_c(t)[/math] заранее заданного аналитиком радиуса, и 0 в противном случае. Функция [math]h(t)[/math] равна [math]\alpha(t)[/math] для BMU и уменьшается с удалением от BMU.

Задание [math]\alpha[/math]

Функция обучения обычно задается следующим образом

• [math]\alpha(t)=\alpha_0 \cdot \exp(\frac{-t}{\tau_\alpha})[/math]

• [math]\alpha(t)=\alpha_0 \cdot (1-\frac{t}{T})[/math]

1.3 Вычислительное ядро алгоритма

Вычислительная сложность SOM как правило, высока, что зависит от конструкции слоя, участвующего в алгоритме;

Шаги 2-4 повторяются много раз для каждого документа и, таким образом, составляют большую часть времени обработки требуется. Шаги 3 (вычисление расстояния до всех узлов) и 4 (весовые коэффициенты обновления) требуют итераций всех координат входного вектора.

Вычислительная сложность сети SOM

[math]O(dN^2)[/math], 

где [math]N[/math] –число векторов в обучающей выборке , [math]d[/math] – размерность входных векторов.

1.4 Макроструктура алгоритма

Некоторые алгоритмы, относящиеся к семейству Кохонена могут быть суммированы следующими тремя фазами:

• Фаза [math] D [/math]: вычисляет расстояние между входом и вектором весовых коэффициентов с помощью уравнения в шаге 1 и возвращает матрицу [math] D [/math]
• Фаза [math] W [/math]: вычисляет нейрон-победителя уравнением в шаге 2, и возвращает вектор [math] b [/math]
• Фаза [math] U [/math]: обновляет вес по уравнению в шаге 3, используя уравнение для функции соседства.

Также выполняются такие макрооперации как:

• умножение вектора на скаляр
• поиск минимального элемента
• сложение векторов
• скалярное произведение векторов

1.9 Входные и выходные данные алгоритма

Входные данные алгоритма:

• [math]\{X_i\}\in\mathfrak{R}^n[/math] - обучающая выборка
• [math]h_{kc}[/math] -
• [math]\alpha[/math]

1.10 Свойства алгоритма

Свойство сохранения топологии означает, что карта Кохонена распределяет сходные векторы входных данных по нейронам, т.е. точки, расположенные в пространстве входов близко друг к другу, отображаются на близко расположенные элементы карты. Таким образом, карта Кохонена может служить как средством кластеризации, так и средством визуального представления данных большой размерности.

Упорядоченное отображение элементов данных облегчает понимание структур в наборе данных.

Визуализация кластеров.

Структура кластера в наборе данных могут быть представлена видимым путем, с помощью отображения расстояния между базисными векторами соседних блоков.