Участник:Александр Куваев/Алгоритм кластеризации, основанный на максимизации ожидания: различия между версиями
| Строка 24: | Строка 24: | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| + | Пусть заданы <math>l</math> объектов <math>x_{1},...,x_{l}</math>, каждый из которых описывается <math>n</math> числовыми признаками. Таким образом, определена матрица объектов-признаков <math>X \in \R^{l \times n}</math>. Предполагается, что объекты выбраны случайно и независимо из смеси <math>n</math>-мерных нормальных распределений с фиксированным числом компонент <math>k</math>. Плотность распределения на множестве объектов имеет вид: | ||
| + | |||
| + | <math>p(x)=\sum_{j=1}^{k}w_{j}p_{j}(x), \sum_{j=1}^{k}w_{j}=1, w_{j} \ge 0 </math>, где <math>p_{j}</math> - плотность распределения <math>j</math>-й компоненты смеси. | ||
| + | |||
| + | Каждая компонента смеси описывается <math>n</math>-мерным вектором математических ожиданий <math>\mu_{j}</math> и матрицей ковариации <math>\Sigma_{j}</math> порядка <math>n</math>, <math>j = 1...k</math>. | ||
| + | |||
| + | '''Исходные данные:''' матрица объектов-признаков <math>X</math>, число кластеров <math>k</math>, максимальное число итераций <math>imax</math>. | ||
| + | |||
| + | '''Вычисляемые данные:''' набор оценок весов, математических ожиданий и ковариационных матриц компонент смеси <math>\theta = (w_{1},...,w_{k}; \; \mu_{1},...,\mu_{k}; \; \Sigma_{1},...,\Sigma_{k})</math>. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
Версия 04:45, 13 октября 2016
Авторы описания: Куваев А.С. и Щенявская Е.В.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Задача кластеризации заключается в разбиении входного множества объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались друг от друга.
Решение этой задачи принципиально неоднозначно по следующим причинам:
- результат кластеризации зависит от способа задания меры сходства объектов выборки
- не существует однозначно наилучшего критерия качества кластеризации
- число кластеров, как правило, неизвестно заранее и задается из некоторых априорных соображений (хотя существуют алгоритмы, способные определять число кластеров автоматически)
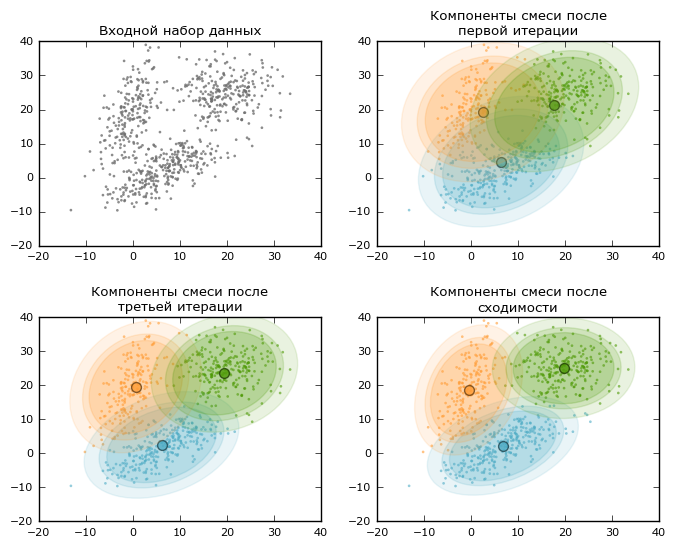
По описанной выше причине существует большое число алгоритмов кластеризации, приводящих к различным разбиениям исходного множества объектов. На этой странице представлено описание одного из таких методов — EM-алгоритма. EM-алгоритм опирается на предположение о вероятностной природе данных: элементы выборки получены случайно и независимо из смеси распределений с фиксированным числом компонент [math]k[/math]. Таким образом, плотность распределения на множестве объектов имеет следующий вид:
[math]p(x)=\sum_{j=1}^{k}w_{j}p_{j}(x), \sum_{j=1}^{k}w_{j}=1, w_{j} \ge 0 [/math], где [math]p_{j}[/math] - плотность распределения [math]j[/math]-й компоненты смеси.
Везде в дальнейшем будем предполагать, что [math]p_{j}[/math] имеют вид многомерных нормальных плотностей с произвольной матрицей ковариации: смеси нормальных распределений позволяют аппроксимировать произвольные непрерывные функции плотности с наперед заданной точностью. Результатом работы EM-алгоритма являются оценки априорных вероятностей компонент смеси [math]w_{j}[/math], а также оценки векторов математических ожиданий и матриц ковариации для каждой компоненты.
EM-алгоритм позволяет значительно упростить задачу максимизации правдоподобия выборки путем искусственного введения вспомогательной матрицы скрытых переменных [math]G[/math]. Алгоритм заключается в последовательном повторении шагов E(expectation) и M(maximization):
- На шаге E на основе текущего приближения параметров смеси по формуле Байеса вычисляются ожидаемые значения скрытых переменных [math]g_{ij}[/math] — апостериорные вероятности того, что [math]i[/math]-й объект принадлежит кластеру [math]j[/math].
- На шаге M решается задача максимизации правдоподобия для нахождения следующего приближения параметров смеси на основе текущего приближения и матрицы скрытых переменных, при этом решение этой задачи выписывается в явном виде.
1.2 Математическое описание алгоритма
Пусть заданы [math]l[/math] объектов [math]x_{1},...,x_{l}[/math], каждый из которых описывается [math]n[/math] числовыми признаками. Таким образом, определена матрица объектов-признаков [math]X \in \R^{l \times n}[/math]. Предполагается, что объекты выбраны случайно и независимо из смеси [math]n[/math]-мерных нормальных распределений с фиксированным числом компонент [math]k[/math]. Плотность распределения на множестве объектов имеет вид:
[math]p(x)=\sum_{j=1}^{k}w_{j}p_{j}(x), \sum_{j=1}^{k}w_{j}=1, w_{j} \ge 0 [/math], где [math]p_{j}[/math] - плотность распределения [math]j[/math]-й компоненты смеси.
Каждая компонента смеси описывается [math]n[/math]-мерным вектором математических ожиданий [math]\mu_{j}[/math] и матрицей ковариации [math]\Sigma_{j}[/math] порядка [math]n[/math], [math]j = 1...k[/math].
Исходные данные: матрица объектов-признаков [math]X[/math], число кластеров [math]k[/math], максимальное число итераций [math]imax[/math].
Вычисляемые данные: набор оценок весов, математических ожиданий и ковариационных матриц компонент смеси [math]\theta = (w_{1},...,w_{k}; \; \mu_{1},...,\mu_{k}; \; \Sigma_{1},...,\Sigma_{k})[/math].