Участник:ЕкатеринаКозырева/Алгоритм динамической иерархической кластеризации CHAMELEON

Алгоритм динамической иерархической кластеризации CHAMELEON
Последовательный алгоритм
Последовательная сложность	[math]O(nm + n log n + m^2 log m)[/math]
Объём входных данных	[math]\frac{n (n - 1)}{2}[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math][/math]
Ширина ярусно-параллельной формы	[math][/math]

Автор описания Е.А.Козырева

1 часть. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм CHAMELEON был предложен в 1999 году тремя учеными из университета Миннесоты – George Karypis, Eui-Hong (Sam) Han и Vipin Kumar[1].

Предназначен для решения задач кластеризации. Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны.

CHAMELEON - это агломеративный иерархический алгоритм кластеризации, ключевой особенностью которого является то, что он учитывает и взаимную связность, и сходство при определении наиболее похожей пары подкластеров, основываясь на динамической модели. Это означает, что в процессе кластеризации два кластера объединяются, только если их относительная взаимная связность и относительное взаимное сходство являются высокими по отношению к внутренней взаимосвязанности кластеров и близости элементов внутри кластеров. Кроме того, Хамелеон использует подход для моделирования степени взаимосвязанности и близости между каждой парой кластеров, который учитывает внутренние характеристики самих кластеров. Таким образом, он может автоматически адаптироваться к внутренним характеристикам объединяемых кластеров.

CHAMELEON находит кластеры в наборе данных с помощью трехфазного алгоритма. На первой фазе происходит построение графа, путём добавления рёбер по принципу k ближайших соседей. На второй фазе CHAMELEON группирует полученные элементы в множество относительно небольших подкластеров. Во время третьей фазы применяется агломеративный иерархический алгоритм кластеризации, с помощью которого находятся естесственные кластеры путем многократного объединения подкластеров, полученных на прошлом этапе.

1.2 Математическое описание алгоритма

Исходные данные:

• Множество из n точек [math]V= {v_{ij}}[/math] в метрическом пространстве, которое задано симметрической матрицей расстояний [math]A[/math] размера [math]n\times n[/math].
• [math]k[/math] - количество ближайших соседей для вершин, [math]k \in N, k \leq n[/math].
• [math]l[/math] - наименьшее число вершин, которое может содержать наибольший подграф на 2-м этапе, [math]l \in N, l \leq n[/math].

Обозначения:

• [math]G = (V, E)[/math] - граф, полученный путём соединения каждой точки с её [math]k[/math] ближайшими соседями.

• [math]K= \{K_{i}\}[/math] - разбиение множества V на набор попарно непересекающихся связных подмножеств, полученное в результате выполнения второй фазы алгоритма.

• [math]G_{2} = (K, E_{2})[/math] - взвешенный граф, вершинами которого являются получившиеся подграфы, а ребрами - количество ребер исходного графа, соединяющих соответствующие подграфы.

• [math]C = \{C_{i}\}[/math] - итоговое разбиение множества вершин графа [math]G_{2}[/math] на набор кластеров.

Вспомогательные понятия

• [math]EC_{(C_{i},C_{j})}[/math] - абсолютная взаимная связность пары кластеров [math]C_{i}, C{j}[/math]. Определяется как сумма весов ребер, соединяющих вершины, принадлежащие [math]C{i}[/math] c вершинами из [math]C{j}[/math]. Внутренняя связность [math]EC_{(C_{i},C_{i})}[/math] вычисляется как сумма ребер, входящих в разделитель, разбивающий [math]C{i}[/math] на два равных подграфа.

• [math]RI_{(C_{i},C_{j})} = \frac{|EC_{(C_{i},C_{j})}|}{(|EC_{C_{i}}|+|EC_{C_{j}}|)/2}[/math] - относительная взаимная связность пары кластеров [math]C_{i}, C{j}[/math]

• [math]S_{EC_{(C_{i},C_{j})}}[/math] - абсолютное взаимное сходство пары кластеров [math]C_{i}, C{j}[/math]. Подсчитывается как среднее сходство между соединенными вершинами, принадлежащими [math]C{i}[/math] и [math]C{j}[/math] соответственно. Соединения обусловлены разбиением общего графа, полученного на первом этапе алгоритма.

• [math] RC_{(C_{i},C_{j})}= \frac{S_{EC_{(C_{i},C_{j})}}}{\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{i})}}+\frac{|C_{i}|}{|C_{i}+C_{j}|}*S_{EC_{(C_{j})}}}[/math] - относительное взаимное сходство пары кластеров [math]C_{i}, C{j}[/math]. Определяется как абсолютное сходство между этой парой кластеров, нормализованное с учетом их внутреннего сходства.

Вычисляемые данные:

[math]U = (u_1, u_2, ..., u_n)[/math] - n-мерный вектор, где [math]u_i \in N_{[C]}[/math] - порядковый номер кластера, к которому принадлежит вершина i исходного множества V.

[math][/math]

Первый этап

На первом этапе, согласно графо-ориентированному подходу, происходит построение графа [math]G = (V, E)[/math] на матрице сходства объектов по принципу k ближайших соседей. Две вершины такого графа соединяет ребро, если объект, соответствующий любой из этих вершин попадает в число k наиболее близких объектов для объекта, соответствующего другой вершине из данной пары.

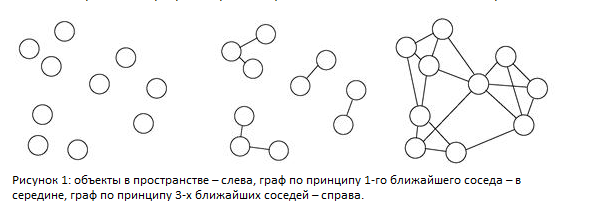
Второй этап

Алгоритм разделяет полученный граф на множество сравнительно малых подграфов [math]K= \{K_{i}\}[/math]. Разделение происходит последовательно. На каждом шаге выбирается подграф, содержащий наибольшее число вершин. Этот граф разделяется на два подграфа так, что разделитель ребер графа минимален и каждый из получаемых подграфов содержит не менее 25 % вершин исходного графа. Процесс разделения останавливается, когда наибольший подграф содержит меньше некоторого заданного числа вершин. Обычно величина этого параметра задается равной значению от 1 до 5 % от числа объектов. Полученное множество связных графов считается множеством начальных кластеров, на котором требуется провести последовательное иерархическое объединение.

Третий этап

Третий этап заключается в итеративном преобразовании множества подграфов [math]K= \{K_{i}\}[/math] в множество кластеров [math]C = \{C_{i}\}[/math]. Алгоритм осуществляет агломеративную иерархическую кластеризацию на основании показателей [math]EC_{(C_{i},C_{j})}[/math], [math]S_{EC_{(C_{i},C_{j})}}[/math], [math]RI_{(C_{i},C_{j})} [/math], [math] RC_{(C_{i},C_{j})}[/math]. Существует две стратегии анализа показателей сходства. Первая подразумевает наличие некоторых пороговых значений [math]T_{RI}[/math] и [math]T_{RC}[/math]. В соответствии с этой стратегией, алгоритм для каждого кластера [math]C_{i}[/math] проверяет, отвечают ли смежные (наиболее близкие) ему кластеры условиям:

• [math]RI_{(C_{i},C_{j})} \geqslant T_{RI}[/math]

• [math]RC_{(C_{i},C_{j})} \geqslant T_{RC}[/math]

Если более одного смежного кластера отвечает этим условиям, то алгоритм выбирает для объединения наиболее связный кластер (граф), то есть такой кластер [math]C_{j}[/math], с которым у кластера [math]C_{i}[/math] получается наибольшая абсолютная взаимная связность. По завершению прохода по всем кластерам, созданные таким образом пары объединяются. Параметры [math]T_{RI}[/math] и [math]T_{RC}[/math] могут использоваться для изменения характеристик получаемых кластеров.

Вторая стратегия заключается в использовании специальной функции, объединяющей понятия относительной взаимной связности и относительного взаимного сходства. На каждом шаге выбираются те кластеры для объединения, которые максимизируют эту функцию:

[math]RI_{(C_{i},C_{j})}*RC_{(C_{i},C_{j})}^\alpha[/math],

где [math]\alpha[/math] выбирается пользователем. Если [math]\alpha \gt 1 [/math], то алгоритм придает большее значение относительному взаимному сходству, а если [math]\alpha \lt 1 [/math], то большее значение имеет относительная взаимная связность.

1.9 Входные и выходные данные алгоритма

Входные данные

1. Симметрическая матрица [math]A[/math] расстояний между элементами данных размера [math]n\times n[/math] с нулями на главной диагонали ([math]a_{ii}= 0, i = 1, \ldots, N[/math]).

2. [math]k[/math] - количество ближайших соседей для вершин (рекомендуемое значение [math]k[/math] от 5 до 20 в зависимости от количества анализируемых объектов).

3. [math]l[/math] - наименьшее число вершин, которое может содержать наибольший подкластер на 2-м этапе . Величина этого параметра варьируется от 1 до 5 % от общего числа объектов.

Объём входных данных

[math]\frac{n (n - 1)}{2}[/math] (в силу симметричности и нулевой главной диагонали достаточно хранить только над/поддиагональные элементы).

Выходные данные

Вектор из [math]n[/math] чисел [math]u_{1}, u_{2}, \ldots, u_{N}[/math], где [math]u_{i}[/math] - целое число, соответствующее кластеру [math]i[/math]-го объекта.

Объём выходных данных

[math]n[/math]

3 Литература

[1] George Karypis, Eui-Hong (Sam) Han и Vipin Kumar, «Chameleon: Hierarchical Clustering Using Dynamic Modeling», 1999.

[2] http://studopedia.ru/7_41934_algoritm-dinamicheskoy-ierarhicheskoy-klasterizatsii-CHAMELEON.html