Участник:Екатерина/Алгоритм устойчивой кластеризации с использованием связей

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задача кластеризации заключается в следующем. Имеется множество [math]n[/math] объектов [math]S=\{s_1,\ldots,s_n\}[/math] и функция расстояния/сходства между объектами [math]\rho (x_i,x_j)[/math]. Требуется разбить множество [math]S[/math] на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из объектов, близких по метрике [math]\rho[/math], а объекты разных кластеров существенно отличались. При этом каждому объекту [math]s\in S[/math] приписывается метка(номер) кластера [math]y_i[/math].

Алгоритм кластеризации - это функция [math]f:X\to Y[/math], которая каждому объекту [math]s\in S[/math] ставит в соответствие метку кластера [math]y\in Y[/math].

Кластеризация - процесс объединения объектов, имеющих похожие характеристики, в непересекающиеся группы, называемые кластерами, так чтобы каждый кластер состоял из подобных объектов, а объекты разных кластеров отличались. При этом каждый объект характеризуется рядом признаков. Решение задачи кластеризации неоднозначно. Поэтому существует несколько типов алгоритмов кластеризации:

• эвристические графовые алгоритмы;
• статистические алгоритмы;
• иерархические алгоритмы.

Иерархические алгоритмы кластеризации строят не одно разбиение на непересекающиеся классы, а систему вложенных разбиений. Различают 2 основных типа: дивизимные и алгомеративные алгоритмы. В алгомеративной иерархической кластеризации объекты объединяются во все более и более крупные кластеры.

Одним из алгоритмов алгомеративной иерархической кластеризации является алгоритм устойчивой кластеризации с использованием связей (robust clustering using links, ROCK), предложенный Sudipto Guha (Stanford University), Rajeev Rastogi (Bell Laboratories) и Kyuseok Shim (Bell Laboratories) в 2000 году. Этот алгоритм отлично подходит для объектов с категориальными признаками, то есть признаками, принимающими свои значения из некоторого множества.

В 2005 году была предложена быстрая версия этого ROCK-алгоритма "Quick ROCK"(QROCK).

1.2 Математическое описание алгоритма

Входные данные: множество объектов [math]P = \{p_1, \ldots , p_n\}[/math], целое число [math]k[/math], пороговое значение [math]\theta[/math], где [math]0\leq\theta\leq 1[/math].

Необходимо разделить множество [math]P[/math] на [math]k[/math] непересекающиеся кластеры.

Определение 1. Два объекта [math]p_i[/math] и [math]p_j[/math] будут соседями, если они значительно близки друг к другу, то есть [math]p_i[/math] и [math]p_j[/math] являются соседями, если [math]sim(p_i, p_j)\geq \theta[/math].

Мера схожести пары объектов [math]sim(p_i, p_j)[/math] может быть основана на евклидовом расстоянии, коэффициенте Жаккарда или на какой-либо другой неметрической функции схожести. Предполагается, что мера [math]sim[/math] принимает значения от 0 до 1, при этом чем ближе значение меры к 1, тем больше схожи точки. Чаще всего используется мера схожести, основанная на коэффициенте Жаккарда (Jaccard coefficient): [math]sim(p_i,p_j) = \frac{|p_i\cap p_j|}{|p_i\cup p_j|}[/math], где [math]|p_i|[/math] - количество атрибутов в [math]p_i[/math]. Чем больше атрибутов в [math]p_i[/math] и [math]p_j[/math] похожи, тем больше значение [math]|p_i\cap p_j|[/math]. Деление его на [math]|p_i\cup p_j|[/math] гарантирует, что значение [math]\theta[/math] окажется в промежутке от 0 до 1. Таким образом уравнение вычисляет похожесть двух объектов на основе схожести атрибутов, входящих в них.

Определение 2. Назовем функцией связи между объектами функцию [math]link(p_i, p_j)[/math], определяемую как число общих соседей между объектами [math]p_i[/math] и [math]p_j[/math]. Из определения следует, что чем больше значение функции связи, тем вероятнее, что объекты [math]p_i[/math] и [math]p_j[/math] принадлежат одному кластеру.

Определение 3. Назовем функцией связи между кластерами функцию [math]link[C_i, C_j] = \sum_{\begin{smallmatrix}p_q\in C_i,\; p_r\in C_j\end{smallmatrix}}^{ } link(p_{q},p_r)[/math], хранящую число связей между объектами кластеров [math]C_i[/math] и [math]C_j[/math].

Определение 4. Целевая функция качества, использующаяся при выборе кластеров для объединения:

[math] g(C_i, C_j) = \frac{link[C_i,C_j]}{(n_i + n_j)^{1 + 2f(\theta )} - n_i^{1+2f(\theta )} - n_j^{1+2f(\theta )}}[/math], где [math]n_i[/math] - число объектов в кластере [math]C_i[/math], функция [math]f(\theta )[/math] выбирается пользователем, обычно [math]f(\theta ) = \frac{\theta - 1}{\theta + 1}[/math] , [math]n_i^{1+2f(\theta )}[/math] - ожидаемое число связей между парами объектов кластера [math]C_i[/math].

Определение 5. Симметричная матрица [math]A[/math] размерности [math]n[/math] называется матрицей связей, где элемент матрицы [math]a_{ij} = link(p_i,p_j), i = \overline{1,n}, j = \overline{1,n}[/math]

1.3 Вычислительное ядро алгоритма

Основная вычислительная нагрузка в алгоритме приходится на умножение матриц при вычислении числа связей. Оно имеет квадратичную сложность.

Также большую вычислительную нагрузку дает цикл, в котором обновляются локальная и глобальная кучи после объединения двух кластеров в один.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют [math]O(n^2\log n)[/math] обновлений содержимого локальной и глобальной куч.

1.5 Схема реализации последовательного алгоритма

Алгоритм иерархической кластеризации ROCK представлен ниже в виде двух процедур: собственно кластеризации и вычисления связей между точками.

1.5.1 Кластеризация

На вход алгоритм принимает некий набор [math]n[/math] точек [math]S[/math]. Кроме того, заданное значение [math]k[/math] кластеров желаемого разбиения. Изначально каждая точка является отдельным кластером. На шаге 1 вычисляется количество связей между всеми парами точек. На шагах 2 и 3 для каждого [math]s[/math] строится локальная куча [math]q[s][/math]. Локальная куча [math]q[s][/math] содержит те кластеры [math]t[/math], для которых [math]link[s,t][/math] отлична от нуля, причем кластеры в куче упорядочены в порядке убывания, на основе целевой функции качества [math]g(s,t)[/math]. На шаге 4 вычисляется глобальная куча [math]Q[/math], содержащая все текущие кластеры, упорядоченные в порядке убывания на основе [math]g(s,max(q[s]))[/math]. Таким образом на каждом шаге лучший кластер в [math]Q[/math] и соответствующий ему максимальный кластер из [math]q[/math] наилучшая пара кластеров для объединения их в один кластер.

На шаге 5 начинает выполняться цикл [math]while[/math], до тех пор, пока в глобальной куче не останется только [math]k[/math] кластеров. На каждой итерации [math]while[/math]-цикла на шагах 6-9 из [math]Q[/math] извлекается лучший кластер [math]u[/math] и соответствующий ему максимальный кластер [math]v[/math] из локальной кучи и удаляется из [math]Q[/math], так как он будет объединен с [math]u[/math], и больше в ней не нужен. Далее кластеры [math]u[/math] и [math]v[/math] объединяются в новый кластер [math]w[/math].

Далее на шагах 10-15 в цикле [math]for[/math] для каждого кластера, который содержит элементы [math]u[/math] и [math]v[/math] в своей локальной куче, они оттуда удаляются и заменяются на новый кластер [math]w[/math]. Для [math]w[/math] создается новая локальная куча.

На 17 шаге новый кластер добывляется в локальную кучу, а на 18 шаге уничтожаются локальные кучи для [math]u[/math] и [math]v[/math].

[math] \begin{align} &\mathbf{procedure}\ cluster (S,k) \\ &\mathbf{begin} \\ &1.\ \ link := compute\_links(S) \\ &2.\ \ \mathbf{for\ each}\ s\in S\ \mathbf{do} \\ &3.\ \ \ \ q[s] := build\_local\_heap(link,s) \\ &4.\ \ Q := build\_global\_heap(S,q) \\ &5.\ \ \mathbf{while}\ size(Q)\ \gt k\ \mathbf{do}\ \{ \\ &6.\ \ \ \ u := extract\_max(Q) \\ &7.\ \ \ \ v := max(q[u]) \\ &8.\ \ \ \ delete(Q,v) \\ &9.\ \ \ \ w := merge(u,v) \\ &10.\ \ \ \mathbf{for\ each}\ x\ \in \ q[u]\ \cup \ q[v]\\ &11.\ \ \ \ \ link[x,w] := link[x,u]\ +\ link[x,v] \\ &12.\ \ \ \ \ delete(q[x],u);\ delete(q[x],v) \\ &13.\ \ \ \ \ insert(q[x],w,g(x,w));\ insert(q[w],x,g(x,w) \\ &14.\ \ \ \ \ update(Q,x,q[x]) \\ &15.\ \ \ \} \\ &16.\ \ \ insert(Q,w,q[w]) \\ &17.\ \ \ deallocate(q[u]);\ deallocate(q[v]) \\ &18.\ \ \} \\ &\mathbf{end} \end{align} [/math]

1.5.2 Вычисление связей

Для вычисления связи между всеми парами точек в [math]S[/math] рассматривается матрица смежности [math]A[/math] размера [math]n*n[/math], где [math]A[i,j][/math] равна 1 или 0, если [math]i[/math] и [math]j[/math] являются или не являются соседями соответственно. В результате умножения [math]A*A[/math] в позиции [math]A[i,j][/math] получим количество связей между [math]i[/math] и [math]j[/math]. Для умножения матриц использовался алгоритм Штрассена.

[math] \begin{align} &\mathbf{procedure}\ compute\_links(S) \\ &\mathbf{begin} \\ &1.\ \ Compute\ nbrlist[i]\ for\ every\ point\ i\ in\ S \\ &2.\ \ Set\ link[i,j]\ to\ be\ zero\ for\ all\ i,j \\ &3.\ \ \mathbf{for}\ i := 1\ \mathbf{to}\ n\ \mathbf{do}\ \{ \\ &4.\ \ \ \ N := nbrlist[i] \\ &5.\ \ \ \ \mathbf{for}\ j := 1\ \mathbf{to}\ |N| - 1\ \mathbf{do} \\ &6.\ \ \ \ \ \ \mathbf{for}\ l := j+1\ \mathbf{to}\ |N|\ \mathbf{do} \\ &7.\ \ \ \ \ \ \ \ link[N[j],N[l]] := link[N[j],N[l]]+1 \\ &8.\ \ \} \\ &\mathbf{end} \end{align} [/math]

1.6 Последовательная сложность алгоритма

Вычислительная сложность алгоритма складывается из сложности инициализации, вычисления связей и собственно кластеризации.

• Инициализация глобальной кучи выполняется за время [math]O(n)[/math].
• Инициализация локальной кучи также требует [math]O(n)[/math].
• Связи между парой точек можно вычислить за [math]O(n*n^{2.37})[/math] шагов, где сложность [math]O(n^{2.37})[/math] - сложность умножения матриц алгоритмом Штрассена. Но это в случае, когда все являются соседями всем. Однако на практике среднее число соседей [math]m_\alpha [/math] и максимальное число соседей [math]m_m[/math] оказывается значительно меньше [math]n[/math]. С учетом этих параметров сложность можно записать как [math]O(n m_\alpha m_m)[/math].
• В процедуре кластеризации основные вычисления происходят в цикле [math]while[/math]. Сам цикл выполняется [math]O(n)[/math] раз. Внутренний [math]for[/math]-цикл доминирует над сложностью в [math]while[/math]-цикле. Его сложность [math]O(n\log n)[/math], так как размер каждой очереди в худшем случае [math]n[/math] и новый объединенный кластер [math]w[/math] может нуждаться в [math]O(n)[/math] локальных очередей. Следовательно весь [math]while[/math]-цикл выполняется за [math]O(n^2\log n)[/math].

Время работы ROCK-алгоритма равна [math]O(n^2+nm_m m_\alpha + n^2\log n)[/math], где [math]m_m[/math] - максимально возможное количество соседей, [math]m_\alpha[/math] - среднее число соседей, [math]n[/math] - количество объектов.

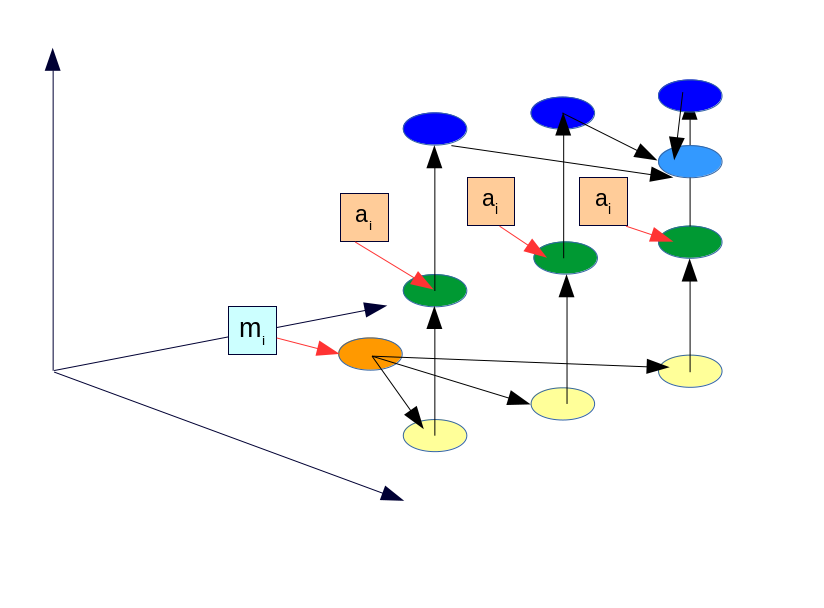
1.7 Информационный граф

Опишем вершины графа алгоритма:

• [math]s_i[/math] - входные данные.
• [math]CML[/math] - процедура, вычисляющая матрицу связей.
• [math]BLH[/math] - функция, строящая начальную локальную очередь для объекта [math]s_i[/math].
• [math]BGH[/math] - строит начальную глобальную очередь входных объектов.
• [math]EM[/math] - достает первый кластер из кучи.
• [math]DL[/math] - удаляет кластер из кучи.
• [math]MG[/math] - производит слияние двух кластеров.
• [math]L[/math] - сумма двух чисел.
• [math]IN[/math] - добавляет в кучу новый элемент учитывая целевую функцию качества.
• [math]U[/math] - обновление кучи учитывая целевую функцию качества.
• [math]FR[/math] - удаление кучи.

Как видно из графа, алгоритм имеет довольно много узких мест. CML - будет записывать данные в одну и ту же матрицу. BGH - функция, строящая глобальную очередь из объектов. Вообще говоря части функций CML и BGH можно распараллелить изнутри, но об этом в следующем разделе.

Также в программе есть вложенные циклы. Внутренний цикл мы можем выполнять параллельно, но вынуждены на каждой итерации делать синхронизацию. Внешний же цикл распараллелить не получится, так как там находятся зависимые по данным операции.

1.8 Ресурс параллелизма алгоритма

Как видно из графа алгоритма, в алгоритме устойчивой кластеризации с использованием связей довольно сильная зависимость по данным. Параллельно обработать можно некоторые отдельные участки кода и только при больших объемах входных данных.

В частности можно выполнять параллельно построение начальной локальной кучи (функция [math]build\_local\_heap[/math]). Т.е. для входа размерности [math]n[/math] и [math]p[/math] процессов, каждый посчитает [math]\frac{n}{p}[/math] локальных куч.

Еще можно выполнять параллельно цикл, связанный обновлением матрицы связей, локальной и глобальной кучи после проведения операции слияния. Но после каждой итерации необходимо делать барьерную синхронизацию для операции [math]update[/math], которая обновляет глобальную кучу.

Как видно из пункту 1.6 сложность последовательного алгоритма была равна [math]O(n^2+nm_m m_\alpha + n^2\log n)[/math]. С учетом распараллеливания описанных выше участков кода на [math]p[/math] процессов, теоретически можно получить время выполнения [math]O(\frac{n^2}{p}+nm_m m_\alpha + \frac{n^2\log n}{p})[/math].

Также стоит отметить, что можно распараллелить процедуру [math]compute\_links[/math], которая умножает матрицы алгоритмом Штрассена. Данный алгоритм имеет смысл выполнять параллельно только если порядок матрицы не менее 1287.

Функции [math]build\_local\_heap[/math] и [math]build\_global\_heap[/math] содержат в себе задачу сортировки, которую также можно выполнить параллельно согласно http://www.intuit.ru/studies/courses/1156/190/lecture/4958 или М. В. Якобовский "Введение в параллельные методы решения задач: Учебное пособие".

Их распараллеливание также может дать некоторое ускорение выполнению алгоритма, но обе функции выполняются ровно один раз.

1.9 Входные и выходные данные алгоритма

Входные данные: на вход подается [math]n[/math] объектов и [math]k[/math] - количество кластеров, на которое необходимо разделить объекты и некоторое пороговое значение [math]\theta[/math], принимающее значение от 0 до 1.

Задаются входные данные в частном случае в виде массива длины [math]n[/math], но так как вообще говоря данные могут иметь не один атрибут, потребуется матрица размера [math]n*r[/math], состоящей из 0 и 1, где [math]r[/math] - количество признаков у объектов, а 0 и 1 стоят в звисимости от того, есть ли такой атрибут у данного объекта или нет.

Выходные данные: Группа кластеризованных данных.

Выходные данные представлены в виде массива из [math]n[/math] элементов, где каждому элементу сопоставлен номер кластера, в который он попал.

1.10 Свойства алгоритма

Отношение последовательной и параллельной сложностей: [math]\frac{O(n^2+nm_m m_\alpha + n^2\log n)}{O(\frac{n^2}{p}+nm_m m_\alpha + \frac{n^2\log n}{p})}[/math].

Алгоритм является детерменированным.

Вычислительная сложность: [math]\frac{O(n^2+nm_m m_\alpha + n^2\log n)}{2n+2}[/math].

ROCK-алгоритм хорошо подходит для категорийных данных, таких как ключевые слова, булевские атрибуты, перечисления и т.п. Он хорошо масштабируем, авторы алгоритма создавали его так, чтобы он хорошо работал на больших объемах данных.

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Алгоритм устойчивой кластеризации с использованием связей реализован в библиотеке CBA в июне 2016 года.

Также он реализован в feed4weka - библиотеке, содержащей алгоритмы для кластеризации данных.