Участник:Зиновьев Владимир/Метод Якоби вычисления собственных значений симметричной матрицы ЗП

Метод Якоби вычисления собственных значений симметричной матрицы ЗП
Последовательный алгоритм
Последовательная сложность	[math]O(n^3)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n^2)[/math]
Ширина ярусно-параллельной формы	[math]2n[/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задача нахождения собственных значений и собственных векторов матриц(СЗВМ) является одной из основных задач для многих разделов физики. С такой вычислительной проблемой приходится сталкиваться, например, при исследовании собственных колебаний различных механических систем, колебательных и электронных спектров молекул и кристаллов. Совершенно принципиальное значение эта проблема приобрела после создания в тридцатых годах прошлого века квантовой механики, которая стала базовой дисциплиной исследования микромира.Кроме того, данная проблема важна в теории автоматического управления, как инструмент исследования устойчивости линейных систем. Метод Якоби приводит симметричную действительную матрицу к диагональной форме с помощью некоторой (в принципе, бесконечной) последовательности плоских вращений в разных плоскостях исходного n-мерного векторного пространства. Метод Якоби состоит из некоторой последовательности шагов, на каждом из которых обнуляется один из недиагональных элементов (обычно наибольший по модулю), в результате чего старая матрица [math]A_{i}[/math] преобразуется в некоторую новую матрицу [math]A_{i+1}[/math]. Делается это с помощью преобразования подобия, использующего матрицу плоского вращения [math]J_{i}[/math] (подробное описание матрицы плоского вращения приведено ниже в разделе "Математическое описание алгоритма"), которая изменяет лишь две координаты [math]n[/math]-мерных векторов, а именно, координаты с номерами [math]j[/math] и [math]k[/math]. При таком шаге матрица [math]A_{i+1}[/math] отличается от матрицы [math]A_{i}[/math] лишь элементами двух строк с номерами [math]j[/math], [math]k[/math] и двух столбцов с теми же номерами ([math]j[/math] и [math]k[/math]). Все же другие элементы матрицы A остаются неизменными. Число шагов, за которое матрица A приводится таким способом к диагональной форме, в общем случае является бесконечным. (это свойство метода Якоби более подробно рассмотрено в разделе "Свойства алгоритма") В результате метод Якоби представляет собой некоторый бесконечный итерационный процесс, на каждом шаге которого преобразующаяся матрица становится всё более и более близкой к диагональной форме (в смысле уменьшения суммы квадратов всех своих недиагональных элементов). На практике обычно выбирается заранее заданная погрешность [math]\varepsilon[/math] и процесс приведения исходной матрицы к диагональному виду прекращается, когда наибольший по модулю внедиагональный элемент матрицы становится меньше [math]\varepsilon[/math]. Таким образом, применяя на практике метод Якоби, мы приводим исходную матрицу к диагональной форме с точностью до некоторой вычислительной погрешности [math]\varepsilon[/math] в результате конечного числа шагов. Повышение этой точности требует увеличения числа шагов метода Якоби. В конечном итоге у полученной в результате этого процесса матрицы на диагонали будут находиться все собственные значения (с определённой погрешностью) исходной симметрической матрицы.

1.1.1 Симметричность матрицы

Симметричность матрицы позволяет хранить и вычислять только чуть больше половины её элементов, что почти вдвое экономит как необходимые для вычислений объёмы памяти, так и количество операций в сравнении с, например, разложением по методу Гаусса.

1.2 Математическое описание алгоритма

Пусть [math]A = A_0[/math] — симметричная матрица. В методе Якоби для [math]A_0[/math] строится последовательность ортогонально подобных матриц [math]A_1, A_2,...[/math], которая в конечном счёте сходится к диагональной матрице, у которой диагональными элементами являются все собственные значения матрицы [math]A[/math]. Матрица [math]A_{i}[/math] получается из матрицы [math]A_{i-1}[/math] по формуле

  [math]A_{i}=J^{T}_iA_{i-1}J_i ,[/math]

где [math]J_i[/math] - ортогональная матрица, называемая вращением Якоби. Таким образом,

  [math]A_{m}=J^{T}_{m-1}A_{m-1}J_{m-1}[/math]
       [math]=J^{T}_{m-1}J^{T}_{m-2}A_{m-2}J_{m-2}J_{m-1}[/math]
       [math]=J^{T}_{m-1}...J^{T}_{0}A_{0}J_{0}...J_{m-1}[/math]
       [math]=J^{T}AJ[/math]

При подходящем выборе вращений [math]J_i[/math] матрица [math]A_m[/math] для больших [math]m[/math] будет близкой к диагональной матрице [math]\Lambda[/math] . Таким образом, [math]\Lambda \approx J^{T}AJ[/math] или [math]J\Lambda J^{T} \approx A[/math], следовательно, столбцы матрицы [math]J[/math] являются собственными значениями матрицы [math]A[/math]. Матрица [math]J_i[/math] выбирается таким образом, чтобы сделать нулями пару внедиагональных элементов матрицы [math]A_{i+1}=J^{T}_{i}A_{i}J_{i}[/math]:

                                                                             [math]j[/math]                         [math]k[/math]

[math] J_i = R(j,k,\theta) \equiv \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} [/math] [math] \begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix} [/math]

Угол вращения [math]\theta[/math] выбирается так, чтобы элементы [math](j,k)[/math] и [math](k,j)[/math] в [math]A_{i+1}[/math] стали нулями. Для того, чтобы найти [math]\theta[/math], составляется уравнение:

[math] \begin{bmatrix} a^{i+1}_{jj}&a^{i+1}_{jk}\\ a^{i+1}_{kj}&a^{i+1}_{kk}\\ \end{bmatrix} = \begin{bmatrix} \cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta)\\ \end{bmatrix}^T \begin{bmatrix} a^{i}_{jj}&a^{i}_{jk}\\ a^{i}_{kj}&a^{i}_{kk}\\ \end{bmatrix} \begin{bmatrix} \cos(\theta)&-\sin(\theta)\\ \sin(\theta)&\cos(\theta)\\ \end{bmatrix} = \begin{bmatrix} \lambda_1&0\\ 0&\lambda_2\\ \end{bmatrix} , [/math]

где [math]\lambda_1[/math] и [math]\lambda_2[/math] - собственные значения подматрицы

[math] \begin{bmatrix} a^{i}_{jj}&a^{i}_{jk}\\ a^{i}_{kj}&a^{i}_{kk}\\ \end{bmatrix} . [/math]

Пусть [math]c = \cos(\theta)[/math] и [math]s = sin(\theta)[/math], [math]a^{i}_{lk} = a_{lk}[/math]. Тогда из предыдущего равенства получаем

[math] \begin{bmatrix} \lambda_1&0\\ 0&\lambda_2\\ \end{bmatrix} = \begin{bmatrix} a_{jj}c^2 + a_{kk}s^2+2sca_{jk}&sc(a_{kk} - a{jj}) + a_{jk}(c^2-s^2)\\ sc(a_{kk} - a{jj}) + a_{jk}(c^2-s^2)&a_{jj}s^2 + a_{kk}c^2-2sca_{jk}\\ \end{bmatrix} . [/math]

Приравнивая внедиагональный элемент к нулю, получаем

[math] \frac{a_{jj} - a{kk}}{2a_{jk}} = \frac{c^2-s^2}{2sc} = ctg(2\theta) = r. [/math]

Пусть [math]tg(\theta) = t = \frac{s}{c}[/math] . Заметим, что выполняется квадратное уравнение [math]t^2 + 2rt - 1 = 0[/math] . Решая уравнение, получаем [math]t = \frac{sign(r)}{|r| + \sqrt{1+r^2}}[/math] . Следовательно [math]c = \frac{1}{\sqrt{1+t^2}}[/math], [math]s = ct[/math]

1.3 Вычислительное ядро алгоритма

На отдельной итерации вычислительным ядром является вычисление новых значений элементов матрицы. Конкретно, изменяются 2 строки и 2 столбца матрицы. Однако в целом, можно отметить, что число операций в алгоритме во многом определяется общую числом итераций, а оно квадратично, в то время как отдельная итерация имеет линейную сложность.

1.4 Макроструктура алгоритма

На макроуровне имеет смысл выделять следующие блоки алгоритма:

1) Блок вычисления параметров вращения на текущей итерации (выбор обнуляемого элемента и расчет угла вращения).

2)Блок, реализующий непосредственно вращение Якоби.

1.5 Схема реализации последовательного алгоритма

1)Находится максимальный наддиагональный элемент [math]a_{jk}[/math] матрицы [math]A[/math].

2)Вычисляются параметры вращения Якоби:

  [math]\tau= \frac{(a_{jj}-a_{kk})}{2a_{jk}}[/math]
  [math]t=sign(\tau)(|\tau|+\sqrt{1+\tau^2})[/math]
  [math]c= \frac{1}{1+\sqrt{1+\tau^2}}[/math]
  [math]s=c*t[/math]

3)К текущей матрице А применяются вращения с вычисленными параметрами:

  [math]A=R^T(j,k,\theta)*A*R(j,k,\theta)[/math]

Стоит отметить, что вычисленные на предыдущем шаге [math]c[/math] и [math]s[/math] есть [math]\cos {\theta}[/math] и [math]\sin {\theta}[/math] соответственно.

4)Если матрица А не достаточно близка к диагональной, происходит переход к шагу 1.

Стоит отметить, что за [math]\frac{n*(n-1)}{2}[/math] итераций алгоритма гарантируется получение результата, т.к. сумма квадратов наддиагональных элементов матрицы А на каждой итерации уменьшается на [math]a_{jk}^2[/math].

1.6 Последовательная сложность алгоритма

Сначала оценим сложность одной итерации:

1)Так как элементы матрицы никак не упорядоченны, поиск наибольшего элемента линейно зависит от числа элементов над диагональю. Конкретнее, на данном шаге происходит [math]\frac{n*(n-1)}{2} -1[/math] сравнение.

2)3 операции деления, 2 операции взятия корня, 4 операции умножения и 4 операции сложения/вычитания.

3)[math]4*n[/math] операций умножения и [math]2*n[/math] операций сложения.

4)операция сравнения

В наиболее неудачном случае количество итераций равняется числу наддиагональных элементов, т.е. [math]\frac{n*(n-1)}{2}[/math]. Таким образом, суммарная сложность алгоритма составляет [math]O(N^4)[/math] сравнений, и [math]O(N^3)[/math] сложений и умножений.

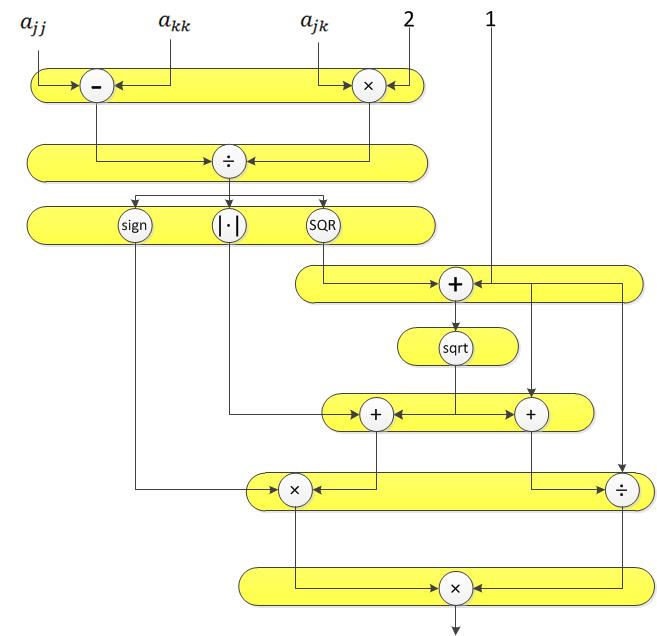
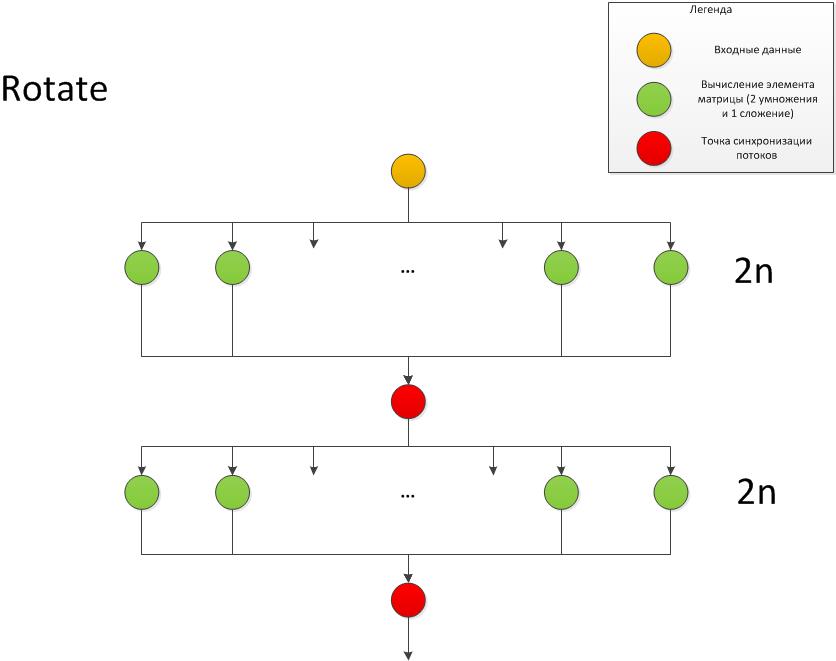
1.7 Информационный граф

Рисунок 1. Граф алгоритма на макроуровне. Rarams - вычисление параметров, Rotate - получение [math]A_{i+1}[/math] из [math]A_{i}[/math].

Рисунок 2. Структура блока Params.

Рисунок 3. Структура блока Rotate.

1.8 Ресурс параллелизма алгоритма

Как видно из представления алгоритма в ярусно-параллельной форме ( п.1.7), максимальная ширина ярусов составляет [math]2n[/math] вершин. Для выполнения данного алгоритма в параллельном варианте следует выполнить [math]O(\frac{n(n+1)}{2})[/math] итераций. Рассмотрим отдельную итерацию с точки зрения ярусно-параллельной формы алгоритма.

1)Выполнение *число_ярусов* ярусов с конечным числом операций

2)Выполнение 2 ярусов вычисления элементов в изменяемых строках и столбцах.

На данных двух ярусах осуществляется [math]4n[/math] умножений и [math]2n[/math] сложений. Данный вид параллелизма относится к координатному. Так как каждая последующая итерация алгоритма зависит от предыдущей, их выполнение распараллелить не представляется возможным. Таким образом, при наличии бесконечного числа процессоров, итоговая сложность алгоритма составляет [math]O(\frac{n(n+1)}{2})[/math]

1.9 Входные и выходные данные алгоритма

Входные данные: плотная матрица [math]A[/math] (элементы [math]a_{ij}[/math]); при этом [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math]..

Объём входных данных: [math]\frac{n (n + 1)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). Конкретный вариант хранения данных зависит от реализации. В качестве примеров можно привести хранение в одномерном массиве длины [math]\frac{n (n + 1)}{2}[/math] по строкам своей нижней части, хранение в виде так называемого ступенчатого массива (такой вариант двумерного массива, в котором каждая строка имеет свой размер).

Выходные данные: вектор собственных значений [math]\Lambda[/math] (элементы [math]\lambda_{ij}[/math]) длины [math]n[/math].

1.10 Свойства алгоритма

Параллельная сложность выполнения алгоритма составляет [math]O(\frac{n(n+1)}{2}).[/math] Последовательная сложность выполнения алгоритма составляет [math]O(\frac{n^2(n+1)}{2}).[/math] Таким образом, соотношение сложностей является линейным. Более того, и вычислительная мощность данного алгоритма линейна.

В алгоритме используется примерно в два раза больше операций умножения, чем сложения. Одельно стоит рассмотреть вопрос хранения матрицы А в процессе работы алгоритма. Хранение лишь нижней или верхней части матрицы в виде одномерного массива возможно; более того, хранение в таком виде обеспечивает экономию памяти в 2 раза и защищает от ассиметричности матрицы в результате накопления математических ошибок. Однако, вычисление индексов [math]i[/math] и [math]j[/math] элементов [math]a_{ij}[/math], соответствующих данному номеру [math]k[/math] вообще говоря требует отдельного цикла, что создает дополнительную нагрузку на процессор.

Кроме того, следует отметить следующие особенности алгоритма:

1)Несмотря на то, что выбор наибольшего наддиагонального элемента, как кандидата на обнуление, кажется оптимальным, на самом деле он таковым не является. При таком выборе элемента, на каждой итерации необходимо находить текущий наибольший элемент в матрице, что требует дополнительных [math]\frac{n*(n-1)}{2}[/math] операций сравнения и приводит к увеличению сложности алгоритма до [math]O(n^4)[/math]. Вместо этого рекомендуется перебирать по очереди все наддиагональные элементы, большие заданного параметра. В большинстве случаев от 4 до 8 полных проходов достаточно для приближения исходной матрицы к диагональной.

2)Если при выборе в качестве обнуляемого элемента [math]a_{ij}[/math] элементы [math]a_{ii} = a_{jj}[/math], то, как видно из формул в пунктах выше, матрицы поворота вырождаются в единичные и матрица на данной итерации не изменяется. Это еще один довод в пользу отказа от выбора наибольшего элемента, т.к. в данном случае произойдет зацикливание алгоритма.

2 Программная реализация алгоритма

2.2 Существующие реализации алгоритма

1)Библиотека JACOBI_EIGENVALUE содержит последовательную реализацию алгоритма.

2)В цифровой библиотеке ieee.org приводится аннотация статьи 2012 года, в которой авторы описывают реализацию данного алгоритма на CUDA.

3)

3 Литература

<references \>