Уровень алгоритма

Участник:Почернина Елена/Метод Якоби вычисления сингулярных чисел и векторов: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
 
(не показаны 104 промежуточные версии 4 участников)
Строка 1: Строка 1:
−
Авторы статьи: Почернина Елена (группа 601), Костюкова Светлана (группа 601)
+
{{Assignment|ASA|Frolov}}
  
 +
{{algorithm
 +
| name              = Метод Якоби вычисления сингулярных чисел и векторов
 +
| serial_complexity = <math>O(n^3)</math>
 +
| pf_height        = <math>O(n^2)</math>
 +
| pf_width          = <math>O(n)</math>
 +
| input_data        = <math>n^2</math>
 +
| output_data      = <math>2n^2 + n</math>
 +
}}
 +
Авторы статьи: [[Участник:Почернина Елена|Почернина Елена]], группа 601 (разделы [[#Общее описание алгоритма|1.1]], [[#Математическое описание алгоритма|1.2]], [[#Макроструктура алгоритма|1.4]], [[#Схема реализации последовательного алгоритма|1.5]], [[#Последовательная сложность алгоритма|1.6]], [[#Ресурс параллелизма алгоритма|1.8]], [[#Масштабируемость алгоритма и его реализации|2.4]], [[#Существующие реализации алгоритма|2.7]]), [[Участница:Светлана|Костюкова Светлана]], группа 601 (разделы [[#Вычислительное ядро алгоритма|1.3]], [[#Схема реализации последовательного алгоритма|1.5]], [[#Информационный граф|1.7]], [[#Входные и выходные данные алгоритма|1.9]], [[#Свойства алгоритма|1.10]], [[#Масштабируемость алгоритма и его реализации|2.4]])
  
 
== Свойства и структура алгоритма ==
 
== Свойства и структура алгоритма ==
  
 
=== Общее описание алгоритма ===
 
=== Общее описание алгоритма ===
 +
 +
'''Метод Якоби''' позволяет найти сингулярное разложение плотной матрицы <math>G</math> размера <math>n</math>×<math>n</math>. Такое разложение можно записать в виде <math>G = U\Sigma V^*</math>, где <math>U, V</math> - унитарные (''в вещественном случае - ортогональные'') матрицы размера <math>n</math>×<math>n</math>, <math>\Sigma</math> - диагональная матрица размера <math>n</math>×<math>n</math> с вещественными положительными числами на главной диагонали. Диагональные элементы матрицы <math>\Sigma</math> называются сингулярными числами матрицы <math>G</math>, а столбцы матриц <math>U,V</math> - левыми и правыми сингулярными векторами.
 +
 +
''Неявный''<ref>Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-264)</ref> метод Якоби математически эквивалентен применению метода Якоби вычисления собственных значений к матрице <math>A = G^TG</math>.
 +
Это значит, что на каждом шаге вычисляется вращение Якоби <math>J</math>, с помощью которого матрица <math>G^TG</math> неявно пересчитывется в <math>J^TG^TGJ</math>; вращение выбрано так, чтобы пара внедиагональных элементов из <math>G^TG</math> обратилась в нули в матрице <math>J^TG^TGJ</math>. При этом ни <math>G^TG</math>, ни <math>J^TG^TGJ</math> не вычисляются в явном виде; вместо них вычисляется матрица <math>GJ</math>. Поэтому алгоритм называется ''методом односторонних вращений''.
 +
 
 +
Метод Якоби для вычисления сингулярных чисел и векторов является самым медленным из имеющихся алгоритмов поиска сингулярных чисел и векторов, но тем не менее, интерес к нему сохраняется. Для некоторых некоторых типов матриц <math>G</math> он способен вычислять сингулярные числа и векторы намного точнее, чем другие методы. В частности, метод Якоби вычисляет сингулярные числа матрицы <math>G</math> с высокой точностью, если G может быть представлена в виде <math>G = DX</math>, где <math>D</math> – диагональная матрица, а <math>X</math> – хорошо обусловлена. В этом случае заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, в то время как другие алгоритмы включают в себя приведение матрицы к двухдиагональной форме, из-за чего и теряют все верные разряды во всех сингулярных числах, кроме старшего.
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
Строка 10: Строка 26:
  
 
Вычисляемые данные: матрица <math>\Sigma = diag(\sigma_{i})</math>, где <math>\sigma_{i}</math> - сингулярные числа, <math>U</math> - матрица левых сингулярных векторов, <math>V</math> - матрица правых сингулярных векторов.
 
Вычисляемые данные: матрица <math>\Sigma = diag(\sigma_{i})</math>, где <math>\sigma_{i}</math> - сингулярные числа, <math>U</math> - матрица левых сингулярных векторов, <math>V</math> - матрица правых сингулярных векторов.
 +
 +
Основной алгоритм заключается в следующем<ref>Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-264)</ref>:
 +
 +
Для всех элементов матрицы <math>A^{(i)} = (G^TG)^{(i)}</math>, находящихся вне главной диагонали <math>(a_{12}, a_{13},\dots, a_{1n}, a_{23}, a_{24},\dots, a_{2n},\dots, a_{n-1n})</math> проверяем условие <math>|A_{jk}|<\varepsilon</math>:
 +
Если <math>|A_{jk}^{(i)}| \le \varepsilon</math>, то переходим к следующему элементу,
 +
Если <math>|A_{jk}^{(i)}| > \varepsilon</math>, то нужно выполнить вращение в плоскости <math>(j,k)</math>, после чего перейти к следующей итерации алгоритма.
 +
Если на очередной итерации не было совершено ни одного вращения, значит матрица <math>A</math> стала достаточна близка к диагональной, и можно перейти к вычислению искомых значений:
 +
 +
<math>\sigma_i = ||G(:,i)||_2</math>;
 +
 +
<math>U = [u_1,\dots,u_n]</math>, где <math>u_i = G(:,i)/\sigma_i</math>;
 +
 +
<math>V = J</math>, где <math>J</math> - накопленное произведение вращений Якоби.
 +
 +
Одностороннее вращение в плоскости <math>(j,k)</math> осуществляет процедура '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>''''':
 +
 +
proc '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>'''''
 +
    вычислить <math>a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}</math> и <math>a_{kk} = (G^TG)_{kk}</math>
 +
    if <math>|a_{jk}|</math> не слишком мал
 +
        <math>
 +
        \begin{align}
 +
        \tau &= \frac{a_{jj} - a_{kk}}{2a_{jk}} \\
 +
        t &= \frac{sign(\tau)}{|\tau| + \sqrt{1 + \tau^2}} \\
 +
        c &= \frac{1}{\sqrt{1 + t^2}} \\
 +
        s &= ct \\
 +
        G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}</math>
 +
        if нужны правые сингулярные векторы
 +
            <math>J = JR(j,k,\theta)</math>
 +
        end if
 +
    end if
 +
 +
Здесь <math>R(j,k,\theta)</math> - матрица вращений Якоби. Матрица вращений выбирается так, чтобы обнулить пару внедиагональных элементов<ref>Дж. Деммель «Вычислительная линейная алгебра» (стр. 244-245)</ref>.
 +
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 +
<math>
 +
\begin{matrix}
 +
  &    &      &      & j &        & k &        &    &  \\
 +
\end{matrix}
 +
</math>
 +
 +
<math>
 +
J_i = R(j,k,\theta) =
 +
\begin{matrix}
 +
  \\
 +
  \\
 +
  \\
 +
j \\
 +
  \\
 +
k \\
 +
  \\
 +
  \\
 +
  \\
 +
\end{matrix}
 +
</math> 
 +
<math>
 +
\begin{bmatrix}
 +
  & 1 &  &        &              &        &              &        &    &  \\
 +
  &  & 1 &        &              &        &              &        &    &  \\
 +
  &  &  & \ddots &              &        &              &        &    &  \\
 +
  &  &  &        & \cos(\theta) &        & -\sin(\theta) &        &    &  \\
 +
  &  &  &        &              & \ddots &              &        &    &  \\
 +
  &  &  &        & \sin(\theta) &        & \cos(\theta)  &        &    &  \\
 +
  &  &  &        &              &        &              & \ddots  &    &  \\
 +
  &  &  &        &              &        &              &        & 1  &  \\
 +
  &  &  &        &              &        &              &        &    & 1 \\
 +
\end{bmatrix}
 +
</math>
 +
 +
При совпадении диагональных элементов <math>(a_{jj} = a_{kk})</math> считаем <math>\theta = \frac{\pi}{4}</math>.
 +
 +
Для завершения описания алгоритма, нужно указать критерий останова, то есть объяснить смысл условия ''"если <math>a_{jk}</math> не слишком мал"''. Подходящим критерием останова является условие
 +
<math>\begin{align}
 +
|a_{jk}| \ge \varepsilon\sqrt{a_{jj}a_{kk}}
 +
\end{align}</math>.
  
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
 +
 +
Вычислительное ядро составляют множественные вычисления элементов матрицы <math>a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}</math> и <math>a_{kk} = (G^TG)_{kk}</math>, а также вычисление промежуточной матрицы <math>GR(j, k, \theta)</math> путем умножения исходной матрицы на матрицу вращения Якоби в процессе выполнения процедуры '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>'''''.
 +
 +
После приведения матрицы <math>G^TG</math> к виду, достаточно близкому к диагональному, вычисляются сингулярные числа:
 +
 +
<math>\sigma_i = ||G(:,i)||_2</math>
 +
 +
Матрица левых сингулярных векторов  <math>U = [u_1,..., u_n]</math>:
 +
 +
<math>u_i = G(:,i)/\sigma_i</math>
 +
 +
И (если требуется) матрица правых сингулярных векторов <math>V</math> путем накопления произведения вращений Якоби:
 +
 +
<math>
 +
V = J,
 +
J = JR(j, k, \theta)
 +
</math>
  
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
 +
Основную часть метода составляет процедура односторонних вращений матрицы (процедура '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>'''''). Рассмотрим подробнее структуру этой процедуры.
 +
 +
- Вычисление <math>a_{jk}, a_{jj}, a_{kk} (a_{ij} = (G^TG)_{ij})</math>. В связи с тем, что нет необходимости каждый раз вычислять произведение <math>G^TG</math>, для вычисления каждого элемента требуется <math>n</math> операций умножения и <math>(n-1)</math> операций сложения.
 +
 +
- Вычисление <math>\tau, c, s, t</math> не представляют значительной вычислительной сложности.
 +
 +
- Одностороннее вращение матрицы (умножение входной матрицы на матрицу вращения) требует порядка <math>O(n)</math> операций.
 +
 +
В итоге, процедура '''''One-Sided-Jacobi-Rotation''''' требует <math>O(n)</math> операций.
 +
 +
После выполнения алгоритма односторонних вращений необходимо вычислить искомые матрицы <math>S, U, V</math> (матрица сингулярных чисел и матрицы левых и правых векторов).
 +
 +
- Вычисление сингулярных чисел <math>\sigma_i</math> требует <math>n</math> операций умножения.
 +
 +
- Вычисление <math>U</math> требует <math>O(n^2)</math> операций. Аналогично для матрицы <math>V</math>.
  
 
=== Схема реализации последовательного алгоритма ===
 
=== Схема реализации последовательного алгоритма ===
 +
Метод можно описать следующим образом<ref>Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-263)</ref>:
 +
 +
repeat
 +
    for <math>j=1</math> to <math>n-1</math>
 +
        for <math>k=j+1</math> to <math>n</math>
 +
            обратиться к процедуре '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>'''''
 +
        end for
 +
    end for
 +
пока <math>G^TG</math> не станет достаточно близка к диагональной матрице
 +
Положить <math>\sigma_{i} = ||G(:,i)||_2 </math> (норма <math>i</math>-го столбца в <math>G</math>)
 +
Положить <math>U = [u_{1},\dots, u_{n}]</math>, где <math>u_{i} = G(:,i)/\sigma_{i}</math>
 +
Положить <math>V = J</math>, где <math>J</math> - накопленное произведение вращений Якоби.
 +
 +
Метод Якоби для нахождения сингулярных чисел и векторов матрицы <math>G</math> также использует метод односторонних вращений (процедура '''''One-Sided-Jacobi-Rotation'''''). Алгоритм выглядит следующим образом:
 +
 +
proc '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>'''''
 +
    вычислить <math>a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}</math> и <math>a_{kk} = (G^TG)_{kk}</math>
 +
    if <math>|a_{jk}|</math> не слишком мал
 +
        <math>
 +
        \begin{align}
 +
        \tau &= \frac{a_{jj} - a_{kk}}{2a_{jk}} \\
 +
        t &= \frac{sign(\tau)}{|\tau| + \sqrt{1 + \tau^2}} \\
 +
        c &= \frac{1}{\sqrt{1 + t^2}} \\
 +
        s &= ct \\
 +
        G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}</math>
 +
        if нужны правые сингулярные векторы
 +
            <math>J = JR(j,k,\theta)</math>
 +
        end if
 +
    end if
  
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
 +
Для вычисления сингулярных чисел и векторов матрицы порядка <math>n</math> в последовательном варианте на каждой итерации алгоритма вызывается процедура '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>''''', сложность которой равна <math>O(n)</math>. Так как выбор индексов <math>j</math> и <math>k</math> осуществляется путем перебора внедиагональных элементов матрицы, для полного прохода потребуется <math>\frac{n(n-1)}{2}</math> итераций.
 +
 +
Таким образом, метод Якоби вычисления сингулярных чисел и векторов при классификации по последовательной сложности относится к алгоритмам с ''кубической сложностью''.
  
 
=== Информационный граф ===
 
=== Информационный граф ===
 +
Граф алгоритма состоит из трех групп вершин:
 +
 +
'''Первая''' группа вершин расположена в двумерной области, соответствующая ей операция - вычисление <math>a_{jj}, a_{jk}, a_{kk}</math>.
 +
Естественно введённые координаты области таковы:
 +
* <math>j</math> — меняется в диапазоне от <math>1</math> до <math>n-1</math>, принимая все целочисленные значения;
 +
* <math>k</math> — меняется в диапазоне от <math>j+1</math> до <math>n</math>, принимая все целочисленные значения.
 +
 +
'''Вторая''' группа вершин соответствует вычислению значений <math>c</math> и <math>s</math> для матрицы вращения
 +
 +
'''Третья''' группа вершин соответствует вычислению произведений матриц <math>GR(k,j, \theta)</math> и <math>JR(k,j, \theta)</math>
 +
 +
<center>
 +
<div class="thumb">
 +
<div class="thumbinner" style="width:{{#expr: 3 * (400 + 35) + 4 * (3 - 1) + 8}}px">
 +
<gallery widths=400px heights=400px>
 +
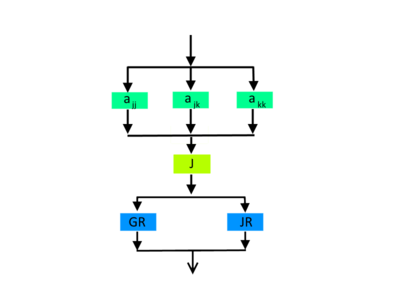
File:JacobiSVG.png|Рисунок 1. Граф одной итерации алгоритма без отображения входных и выходных данных.
 +
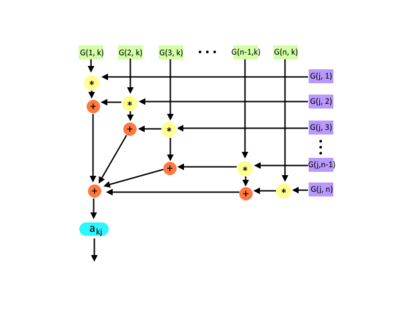
File:Akj.png|Рисунок 2. Граф вычисления значений элементов <math>a_{jj}, a_{jk}, a_{kk}</math>.
 +
</gallery>
 +
<gallery widths=400px heights=1200px>
 +
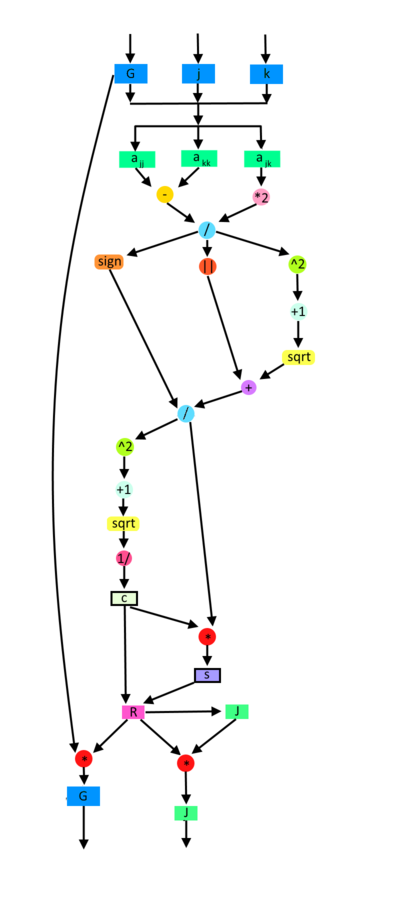
File:JacobiSVD2.png|Рисунок 3. Граф одной итерации алгоритма с вычислением матрицы вращения <math>R</math> отображением входных и выходных данных.
 +
</gallery>
 +
<gallery widths=400px heights=400px>
 +
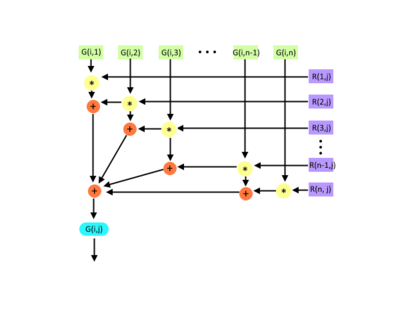
File:Gij.png|Рисунок 4. Граф вычисления значений элементов матрицы <math>GR</math>
 +
File:Jij.png|Рисунок 5. Граф вычисления значений элементов матрицы <math>JR</math>
 +
</gallery>
 +
</div>
 +
</div>
 +
</center>
  
 
=== Ресурс параллелизма алгоритма ===
 
=== Ресурс параллелизма алгоритма ===
 +
В данном алгоритме существует возможность параллельного вычисления вращений Якоби<ref>Halil Snopce, Ilir Spahiu Parallel Computation of the SVD, pp. 458-460, http://www.wseas.us/e-library/conferences/2011/Paris/ECC/ECC-73.pdf</ref><ref>V. Strumpen, H. Hoffmann, A. Agarwal A Stream Algorithm for the SVD, pp. 6-7, 23-24, http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TM-641.pdf</ref>. Максимальное количество вращений в данном методе равно <math>\frac{n(n-1)}{2}</math>. В параллельной реализации, если <math>n</math> - четное, можно выполнить <math>\frac{n}{2}</math> вращений параллельно, если <math>n</math> - нечетное, то <math>\frac{n-1}{2}</math> вращений.
 +
 +
Основную сложность в процедуре вращения '''''One-Sided-Jacobi-Rotation<math>(G,j,k)</math>''''' представляет вычисление элементов <math>a_{jj}, a_{jk}, a_{kk}</math>, которое можно производить параллельно. Вычисление элементов <math>a_{jj}, a_{jk}, a_{kk}</math>  требует порядка <math>O(logN)</math> операций. Вычисление элементов матриц <math>GR, JR</math> в параллельной реализации требует <math>O(1)</math> операций.
 +
 +
Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью <math>O(n^2)</math>, а при классификации по ширине ЯПФ — к алгоритмам со сложностью <math>O(n)</math>.
  
 
=== Входные и выходные данные алгоритма ===
 
=== Входные и выходные данные алгоритма ===
Строка 28: Строка 215:
 
* <math>A= G^TG</math> – симметрическая матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>.
 
* <math>A= G^TG</math> – симметрическая матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>.
  
−
'''Объём входных данных''':  
+
'''Объём входных данных''': <math>n^2</math>
  
 
'''Выходные данные''': матрица <math>\Sigma = diag(\sigma_{i})</math>, где <math>\sigma_{i}</math>  - сингулярные числа, матрица <math>U</math> левых сингулярных векторов и матрица <math>V</math> правых сингулярных векторов.
 
'''Выходные данные''': матрица <math>\Sigma = diag(\sigma_{i})</math>, где <math>\sigma_{i}</math>  - сингулярные числа, матрица <math>U</math> левых сингулярных векторов и матрица <math>V</math> правых сингулярных векторов.
  
−
'''Объём выходных данных''':  
+
'''Объём выходных данных''': <math>2n^2 + n</math> (так как матрица сингулярных чисел <math>\Sigma</math> - диагональная, то достаточно хранить вектор сингулярных чисел (элементы <math>\sigma_i</math>), а также две матрицы <math>U, V</math> левых и правых сингулярных векторов).
  
 
=== Свойства алгоритма ===
 
=== Свойства алгоритма ===
 +
Метод Якоби является самым медленным из имеющихся алгоритмов вычисления сингулярных чисел и сингулярных векторов матрицы. Тем не менее, для некоторых некоторых типов матриц <math>G</math> он способен вычислять сингулярные числа и векторы намного точнее, чем другие методы. Кроме того, в методе Якоби заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, за счет этого метод достигает высокой относительной точности.
 +
 +
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов для метода Якоби является линейным, вычислительная мощность алгоритма также линейна.
 +
 +
Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности (число итераций зависит от входных данных и порогового значения).
  
 
== Программная реализация алгоритма ==
 
== Программная реализация алгоритма ==
 +
 +
=== Особенности реализации последовательного алгоритма ===
 +
 +
=== Локальность данных и вычислений ===
 +
 +
=== Возможные способы и особенности параллельной реализации алгоритма ===
  
 
=== Масштабируемость алгоритма и его реализации ===
 
=== Масштабируемость алгоритма и его реализации ===
 +
 +
==== Масштабируемость алгоритма ====
 +
Оценки предела масштабируемости алгоритма были рассмотрены в разделе [[#Ресурс параллелизма алгоритма|Ресурс параллелизма алгоритма]].
 +
 +
==== Масштабируемость реализации алгоритма ====
 +
Проведём исследование масштабируемости параллельной реализации метода Якоби нахождения сингулярных чисел и векторов. Исследование проводилось на суперкомпьютере "Ломоносов" [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского университета].
 +
 +
Набор и границы значений изменяемых реализации алгоритма:
 +
 +
* число процессоров [1:16] с шагом 1;
 +
* размер матрицы [100 : 900] с шагом 100.
 +
 +
В результате проведенных экспериментов был получен следующий диапазон [[Глоссарий#Эффективность реализации|эффективности реализации]] алгоритма:
 +
 +
* минимальная эффективность реализации: 0.0095%
 +
* максимальная эффективность реализации: 0.929%
 +
 +
При запуске использовалась версия mkl 11.2.0.
 +
 +
Компилятор icc запускался со следующими опциями: -DMKL_ILP64 -qopenmp -I${MKLROOT}/include -Wl,--start-group ${MKLROOT}/lib/intel64/libmkl_intel_ilp64.a ${MKLROOT}/lib/intel64/libmkl_core.a ${MKLROOT}/lib/intel64/libmkl_intel_thread.a -Wl,--end-group -lpthread -lm -ldl
 +
 +
 +
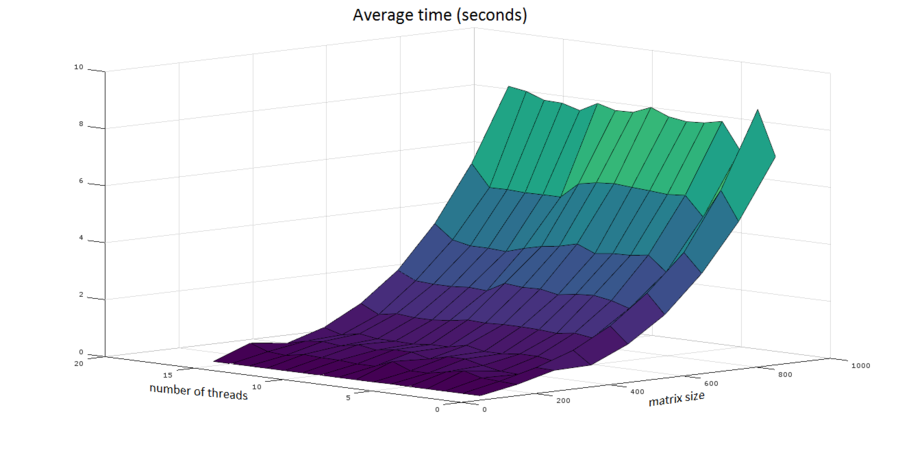
[[File:Averagetime.PNG|center|thumb|900px|Рисунок 6. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение времени выполнения в зависимости от числа процессоров и размера матрицы]]
 +
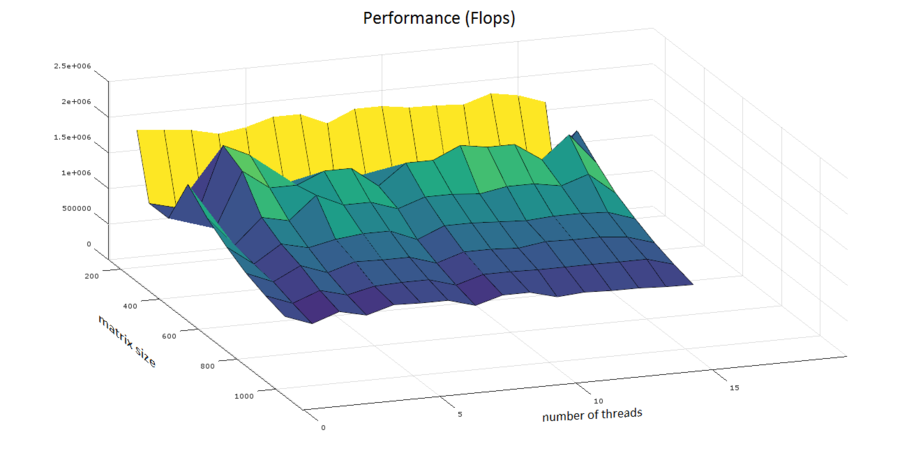
[[File:JacobiPerformance.PNG|center|thumb|900px|Рисунок 7. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение производительности в зависимости от числа процессов и размера матрицы]]
 +
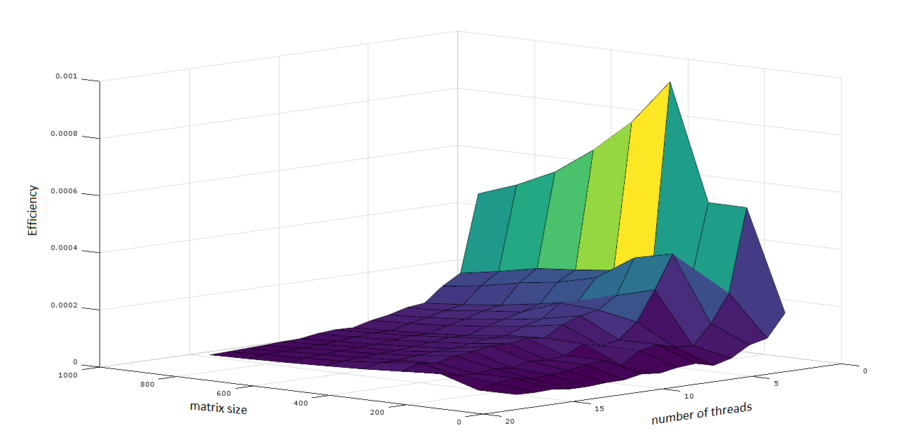
[[File:JacobiEfficiency.PNG|center|thumb|900px|Рисунок 8. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение эффективности в зависимости от числа процессов и размера матрицы]]
 +
 +
Построим оценки масштабируемости реализации метода Якоби вычисления сингулярных чисел и векторов:
 +
* По числу потоков: при увеличении числа потоков эффективность на рассмотренной области увеличивается при переходе от двух потоков к трем. Дальнейшее увеличение количества потоков приводит к снижению эффективности.
 +
* По размеру задачи: наибольшая производительность достигается на матрицах размера 300x300 и 400x400. Дальнейшее увеличение размера матрицы не приводит к увеличению производительности.
 +
 +
[https://software.intel.com/ru-ru/node/521152#248AD4D8-005A-4800-9A73-428952BC1E44 Исследованная параллельная реализация, реализованная в библиотеке Intel MKL]
 +
 +
=== Динамические характеристики и эффективность реализации алгоритма ===
 +
 +
=== Выводы для классов архитектур ===
  
 
=== Существующие реализации алгоритма ===
 
=== Существующие реализации алгоритма ===
−
Метод Якоби нахождения сингулярных значений и векторов реализован в библиотеке Intel MKL.
+
Несмотря на то, что метод Якоби является самым медленным из методов вычисления сингулярных чисел и векторов матрицы, он реализован в некоторых пакетах, например, LAPACK, ScaLAPACK, Intel MKL<ref>Intel® Math Kernel Library, https://software.intel.com/ru-ru/node/521153#CAF8CA08-1C69-48F8-B0C3-B2B27AFA92FA</ref>.
−
В целом, этот не включен во многие пакеты, несмотря на то, что он обеспечивает высокую относительную точность, так как считается самым медленным алгоритмом поиска сингулярных чисел и векторов.
+
 
 
== Литература ==
 
== Литература ==
−
1. Дж. Деммель Вычислительная линейная алгебра. Изд. Мир, 2001.
 

Текущая версия на 15:50, 14 декабря 2016

Symbol confirmed.svgЭта работа успешно выполнена
Преподавателю: в основное пространство, в подстраницу
Данное задание было проверено и зачтено.
Проверено Frolov и ASA.



Метод Якоби вычисления сингулярных чисел и векторов
Последовательный алгоритм
Последовательная сложность [math]O(n^3)[/math]
Объём входных данных [math]n^2[/math]
Объём выходных данных [math]2n^2 + n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(n^2)[/math]
Ширина ярусно-параллельной формы [math]O(n)[/math]

Авторы статьи: Почернина Елена, группа 601 (разделы 1.1, 1.2, 1.4, 1.5, 1.6, 1.8, 2.4, 2.7), Костюкова Светлана, группа 601 (разделы 1.3, 1.5, 1.7, 1.9, 1.10, 2.4)

Содержание

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Якоби позволяет найти сингулярное разложение плотной матрицы [math]G[/math] размера [math]n[/math]×[math]n[/math]. Такое разложение можно записать в виде [math]G = U\Sigma V^*[/math], где [math]U, V[/math] - унитарные (в вещественном случае - ортогональные) матрицы размера [math]n[/math]×[math]n[/math], [math]\Sigma[/math] - диагональная матрица размера [math]n[/math]×[math]n[/math] с вещественными положительными числами на главной диагонали. Диагональные элементы матрицы [math]\Sigma[/math] называются сингулярными числами матрицы [math]G[/math], а столбцы матриц [math]U,V[/math] - левыми и правыми сингулярными векторами.

Неявный[1] метод Якоби математически эквивалентен применению метода Якоби вычисления собственных значений к матрице [math]A = G^TG[/math]. Это значит, что на каждом шаге вычисляется вращение Якоби [math]J[/math], с помощью которого матрица [math]G^TG[/math] неявно пересчитывется в [math]J^TG^TGJ[/math]; вращение выбрано так, чтобы пара внедиагональных элементов из [math]G^TG[/math] обратилась в нули в матрице [math]J^TG^TGJ[/math]. При этом ни [math]G^TG[/math], ни [math]J^TG^TGJ[/math] не вычисляются в явном виде; вместо них вычисляется матрица [math]GJ[/math]. Поэтому алгоритм называется методом односторонних вращений.

Метод Якоби для вычисления сингулярных чисел и векторов является самым медленным из имеющихся алгоритмов поиска сингулярных чисел и векторов, но тем не менее, интерес к нему сохраняется. Для некоторых некоторых типов матриц [math]G[/math] он способен вычислять сингулярные числа и векторы намного точнее, чем другие методы. В частности, метод Якоби вычисляет сингулярные числа матрицы [math]G[/math] с высокой точностью, если G может быть представлена в виде [math]G = DX[/math], где [math]D[/math] – диагональная матрица, а [math]X[/math] – хорошо обусловлена. В этом случае заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, в то время как другие алгоритмы включают в себя приведение матрицы к двухдиагональной форме, из-за чего и теряют все верные разряды во всех сингулярных числах, кроме старшего.

1.2 Математическое описание алгоритма

Исходные данные: матрица [math]G[/math] (элементы [math]g_{ij}, i, j = 1, \ldots, n[/math]).

Вычисляемые данные: матрица [math]\Sigma = diag(\sigma_{i})[/math], где [math]\sigma_{i}[/math] - сингулярные числа, [math]U[/math] - матрица левых сингулярных векторов, [math]V[/math] - матрица правых сингулярных векторов.

Основной алгоритм заключается в следующем[2]:

Для всех элементов матрицы [math]A^{(i)} = (G^TG)^{(i)}[/math], находящихся вне главной диагонали [math](a_{12}, a_{13},\dots, a_{1n}, a_{23}, a_{24},\dots, a_{2n},\dots, a_{n-1n})[/math] проверяем условие [math]|A_{jk}|\lt \varepsilon[/math]: Если [math]|A_{jk}^{(i)}| \le \varepsilon[/math], то переходим к следующему элементу, Если [math]|A_{jk}^{(i)}| \gt \varepsilon[/math], то нужно выполнить вращение в плоскости [math](j,k)[/math], после чего перейти к следующей итерации алгоритма. Если на очередной итерации не было совершено ни одного вращения, значит матрица [math]A[/math] стала достаточна близка к диагональной, и можно перейти к вычислению искомых значений:

[math]\sigma_i = ||G(:,i)||_2[/math];

[math]U = [u_1,\dots,u_n][/math], где [math]u_i = G(:,i)/\sigma_i[/math];

[math]V = J[/math], где [math]J[/math] - накопленное произведение вращений Якоби.

Одностороннее вращение в плоскости [math](j,k)[/math] осуществляет процедура One-Sided-Jacobi-Rotation[math](G,j,k)[/math]: 

proc One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
    вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]
         \begin{align}
         \tau &= \frac{a_{jj} - a_{kk}}{2a_{jk}} \\
         t &= \frac{sign(\tau)}{|\tau| + \sqrt{1 + \tau^2}} \\
         c &= \frac{1}{\sqrt{1 + t^2}} \\
         s &= ct \\
         G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}[/math]
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

Здесь [math]R(j,k,\theta)[/math] - матрица вращений Якоби. Матрица вращений выбирается так, чтобы обнулить пару внедиагональных элементов[3].

                                                                                 [math] \begin{matrix} & & & & j & & k & & & \\ \end{matrix} [/math]

[math] J_i = R(j,k,\theta) = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} [/math] [math] \begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix} [/math]

При совпадении диагональных элементов [math](a_{jj} = a_{kk})[/math] считаем [math]\theta = \frac{\pi}{4}[/math].

Для завершения описания алгоритма, нужно указать критерий останова, то есть объяснить смысл условия "если [math]a_{jk}[/math] не слишком мал". Подходящим критерием останова является условие [math]\begin{align} |a_{jk}| \ge \varepsilon\sqrt{a_{jj}a_{kk}} \end{align}[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро составляют множественные вычисления элементов матрицы [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math], а также вычисление промежуточной матрицы [math]GR(j, k, \theta)[/math] путем умножения исходной матрицы на матрицу вращения Якоби в процессе выполнения процедуры One-Sided-Jacobi-Rotation[math](G,j,k)[/math].

После приведения матрицы [math]G^TG[/math] к виду, достаточно близкому к диагональному, вычисляются сингулярные числа:

[math]\sigma_i = ||G(:,i)||_2[/math]

Матрица левых сингулярных векторов [math]U = [u_1,..., u_n][/math]:

[math]u_i = G(:,i)/\sigma_i[/math]

И (если требуется) матрица правых сингулярных векторов [math]V[/math] путем накопления произведения вращений Якоби:

[math] V = J, J = JR(j, k, \theta) [/math]

1.4 Макроструктура алгоритма

Основную часть метода составляет процедура односторонних вращений матрицы (процедура One-Sided-Jacobi-Rotation[math](G,j,k)[/math]). Рассмотрим подробнее структуру этой процедуры.

- Вычисление [math]a_{jk}, a_{jj}, a_{kk} (a_{ij} = (G^TG)_{ij})[/math]. В связи с тем, что нет необходимости каждый раз вычислять произведение [math]G^TG[/math], для вычисления каждого элемента требуется [math]n[/math] операций умножения и [math](n-1)[/math] операций сложения.

- Вычисление [math]\tau, c, s, t[/math] не представляют значительной вычислительной сложности.

- Одностороннее вращение матрицы (умножение входной матрицы на матрицу вращения) требует порядка [math]O(n)[/math] операций.

В итоге, процедура One-Sided-Jacobi-Rotation требует [math]O(n)[/math] операций.

После выполнения алгоритма односторонних вращений необходимо вычислить искомые матрицы [math]S, U, V[/math] (матрица сингулярных чисел и матрицы левых и правых векторов).

- Вычисление сингулярных чисел [math]\sigma_i[/math] требует [math]n[/math] операций умножения.

- Вычисление [math]U[/math] требует [math]O(n^2)[/math] операций. Аналогично для матрицы [math]V[/math].

1.5 Схема реализации последовательного алгоритма

Метод можно описать следующим образом[4]: 

repeat
    for [math]j=1[/math] to [math]n-1[/math]
        for [math]k=j+1[/math] to [math]n[/math]
            обратиться к процедуре One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
        end for
    end for
пока [math]G^TG[/math] не станет достаточно близка к диагональной матрице
Положить [math]\sigma_{i} = ||G(:,i)||_2 [/math] (норма [math]i[/math]-го столбца в [math]G[/math])
Положить [math]U = [u_{1},\dots, u_{n}][/math], где [math]u_{i} = G(:,i)/\sigma_{i}[/math]
Положить [math]V = J[/math], где [math]J[/math] - накопленное произведение вращений Якоби.

Метод Якоби для нахождения сингулярных чисел и векторов матрицы [math]G[/math] также использует метод односторонних вращений (процедура One-Sided-Jacobi-Rotation). Алгоритм выглядит следующим образом: 

proc One-Sided-Jacobi-Rotation[math](G,j,k)[/math]
    вычислить [math]a_{jj} = (G^TG)_{jj}, a_{jk} = (G^TG)_{jk}[/math] и [math]a_{kk} = (G^TG)_{kk}[/math]
    if [math]|a_{jk}|[/math] не слишком мал
        [math]
         \begin{align}
         \tau &= \frac{a_{jj} - a_{kk}}{2a_{jk}} \\
         t &= \frac{sign(\tau)}{|\tau| + \sqrt{1 + \tau^2}} \\
         c &= \frac{1}{\sqrt{1 + t^2}} \\
         s &= ct \\
         G &= GR(j,k,\theta) \  \dots c=cos\theta, s=sin\theta \end{align}[/math]
        if нужны правые сингулярные векторы 
            [math]J = JR(j,k,\theta)[/math]
        end if
    end if

1.6 Последовательная сложность алгоритма

Для вычисления сингулярных чисел и векторов матрицы порядка [math]n[/math] в последовательном варианте на каждой итерации алгоритма вызывается процедура One-Sided-Jacobi-Rotation[math](G,j,k)[/math], сложность которой равна [math]O(n)[/math]. Так как выбор индексов [math]j[/math] и [math]k[/math] осуществляется путем перебора внедиагональных элементов матрицы, для полного прохода потребуется [math]\frac{n(n-1)}{2}[/math] итераций.

Таким образом, метод Якоби вычисления сингулярных чисел и векторов при классификации по последовательной сложности относится к алгоритмам с кубической сложностью.

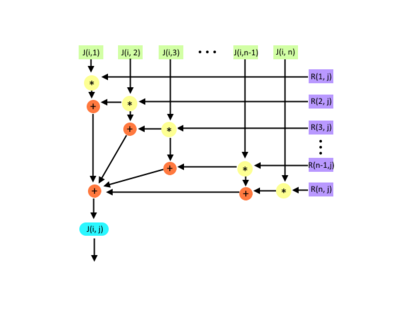
1.7 Информационный граф

Граф алгоритма состоит из трех групп вершин:

Первая группа вершин расположена в двумерной области, соответствующая ей операция - вычисление [math]a_{jj}, a_{jk}, a_{kk}[/math]. Естественно введённые координаты области таковы:

  • [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]n-1[/math], принимая все целочисленные значения;
  • [math]k[/math] — меняется в диапазоне от [math]j+1[/math] до [math]n[/math], принимая все целочисленные значения.

Вторая группа вершин соответствует вычислению значений [math]c[/math] и [math]s[/math] для матрицы вращения

Третья группа вершин соответствует вычислению произведений матриц [math]GR(k,j, \theta)[/math] и [math]JR(k,j, \theta)[/math]

  • Рисунок 1. Граф одной итерации алгоритма без отображения входных и выходных данных.

  • Рисунок 2. Граф вычисления значений элементов [math]a_{jj}, a_{jk}, a_{kk}[/math].

  • Рисунок 3. Граф одной итерации алгоритма с вычислением матрицы вращения [math]R[/math] отображением входных и выходных данных.

  • Рисунок 4. Граф вычисления значений элементов матрицы [math]GR[/math]

  • Рисунок 5. Граф вычисления значений элементов матрицы [math]JR[/math]

1.8 Ресурс параллелизма алгоритма

В данном алгоритме существует возможность параллельного вычисления вращений Якоби[5][6]. Максимальное количество вращений в данном методе равно [math]\frac{n(n-1)}{2}[/math]. В параллельной реализации, если [math]n[/math] - четное, можно выполнить [math]\frac{n}{2}[/math] вращений параллельно, если [math]n[/math] - нечетное, то [math]\frac{n-1}{2}[/math] вращений.

Основную сложность в процедуре вращения One-Sided-Jacobi-Rotation[math](G,j,k)[/math] представляет вычисление элементов [math]a_{jj}, a_{jk}, a_{kk}[/math], которое можно производить параллельно. Вычисление элементов [math]a_{jj}, a_{jk}, a_{kk}[/math] требует порядка [math]O(logN)[/math] операций. Вычисление элементов матриц [math]GR, JR[/math] в параллельной реализации требует [math]O(1)[/math] операций.

Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью [math]O(n^2)[/math], а при классификации по ширине ЯПФ — к алгоритмам со сложностью [math]O(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная матрица [math]G[/math] (элементы [math]g_{ij}[/math]). Дополнительные ограничения:

  • [math]A= G^TG[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math].

Объём входных данных: [math]n^2[/math]

Выходные данные: матрица [math]\Sigma = diag(\sigma_{i})[/math], где [math]\sigma_{i}[/math] - сингулярные числа, матрица [math]U[/math] левых сингулярных векторов и матрица [math]V[/math] правых сингулярных векторов.

Объём выходных данных: [math]2n^2 + n[/math] (так как матрица сингулярных чисел [math]\Sigma[/math] - диагональная, то достаточно хранить вектор сингулярных чисел (элементы [math]\sigma_i[/math]), а также две матрицы [math]U, V[/math] левых и правых сингулярных векторов).

1.10 Свойства алгоритма

Метод Якоби является самым медленным из имеющихся алгоритмов вычисления сингулярных чисел и сингулярных векторов матрицы. Тем не менее, для некоторых некоторых типов матриц [math]G[/math] он способен вычислять сингулярные числа и векторы намного точнее, чем другие методы. Кроме того, в методе Якоби заданная матрица обрабатывается без предварительного приведения к двухдиагональному виду, за счет этого метод достигает высокой относительной точности.

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов для метода Якоби является линейным, вычислительная мощность алгоритма также линейна.

Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности (число итераций зависит от входных данных и порогового значения).

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

Оценки предела масштабируемости алгоритма были рассмотрены в разделе Ресурс параллелизма алгоритма.

2.4.2 Масштабируемость реализации алгоритма

Проведём исследование масштабируемости параллельной реализации метода Якоби нахождения сингулярных чисел и векторов. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых реализации алгоритма:

  • число процессоров [1:16] с шагом 1;
  • размер матрицы [100 : 900] с шагом 100.

В результате проведенных экспериментов был получен следующий диапазон эффективности реализации алгоритма:

  • минимальная эффективность реализации: 0.0095%
  • максимальная эффективность реализации: 0.929%

При запуске использовалась версия mkl 11.2.0.

Компилятор icc запускался со следующими опциями: -DMKL_ILP64 -qopenmp -I${MKLROOT}/include -Wl,--start-group ${MKLROOT}/lib/intel64/libmkl_intel_ilp64.a ${MKLROOT}/lib/intel64/libmkl_core.a ${MKLROOT}/lib/intel64/libmkl_intel_thread.a -Wl,--end-group -lpthread -lm -ldl


Рисунок 6. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение времени выполнения в зависимости от числа процессоров и размера матрицы
Рисунок 7. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение производительности в зависимости от числа процессов и размера матрицы
Рисунок 8. Параллельная реализация метода Якоби вычисления сингулярных чисел и векторов. Изменение эффективности в зависимости от числа процессов и размера матрицы

Построим оценки масштабируемости реализации метода Якоби вычисления сингулярных чисел и векторов:

  • По числу потоков: при увеличении числа потоков эффективность на рассмотренной области увеличивается при переходе от двух потоков к трем. Дальнейшее увеличение количества потоков приводит к снижению эффективности.
  • По размеру задачи: наибольшая производительность достигается на матрицах размера 300x300 и 400x400. Дальнейшее увеличение размера матрицы не приводит к увеличению производительности.

Исследованная параллельная реализация, реализованная в библиотеке Intel MKL

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Несмотря на то, что метод Якоби является самым медленным из методов вычисления сингулярных чисел и векторов матрицы, он реализован в некоторых пакетах, например, LAPACK, ScaLAPACK, Intel MKL[7].

3 Литература

  1. ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-264)
  2. ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-264)
  3. ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 244-245)
  4. ↑ Дж. Деммель «Вычислительная линейная алгебра» (стр. 261-263)
  5. ↑ Halil Snopce, Ilir Spahiu Parallel Computation of the SVD, pp. 458-460, http://www.wseas.us/e-library/conferences/2011/Paris/ECC/ECC-73.pdf
  6. ↑ V. Strumpen, H. Hoffmann, A. Agarwal A Stream Algorithm for the SVD, pp. 6-7, 23-24, http://publications.csail.mit.edu/lcs/pubs/pdf/MIT-LCS-TM-641.pdf
  7. ↑ Intel® Math Kernel Library, https://software.intel.com/ru-ru/node/521153#CAF8CA08-1C69-48F8-B0C3-B2B27AFA92FA
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Почернина_Елена/Метод_Якоби_вычисления_сингулярных_чисел_и_векторов&oldid=20915