Участник:Руфина Третьякова/Хранение ненулевых элементов разреженных матриц. Умножение разреженной матрицы на вектор: различия между версиями
м (Lineprinter переименовал страницу Хранение ненулевых элементов разреженных матриц. Умножение разреженной матрицы на вектор в [[Участник:Ру…) |
|
(нет различий)
| |
Версия 16:09, 28 октября 2016
 | Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 28.10.2016 Авторы этой статьи считают, что задание выполнено. |
| Умножение разреженной матрицы на вектор | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]nnz[/math] |
| Объём входных данных | [math]2(nnz+n)+1[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(n)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Авторы статьи: Третьякова Р. М. (группа 603), Буторина Е. В. (группа 603)
Руфина Третьякова отвечает за программную реализацию алгоритма, Екатерина Буторина - за написание статьи.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Разрежённая матрица — это матрица с преимущественно нулевыми элементами. В противном случае, если бо́льшая часть элементов матрицы ненулевые, матрица считается плотной. Среди специалистов нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разрежённой. Разные авторы предлагают различные варианты. Огромные разрежённые матрицы часто возникают при решении таких задач, как дифференциальное уравнение в частных производных или операции с графами. При хранении и преобразовании разрежённых матриц в компьютере бывает полезно, а часто и необходимо, использовать специальные алгоритмы и структуры данных, которые учитывают разрежённую структуру матрицы. Операции и алгоритмы, применяемые для работы с обычными, плотными матрицами, применительно к большим разрежённым матрицам работают относительно медленно и требуют значительных объёмов памяти. Однако разрежённые матрицы могут быть легко сжаты путём записи только своих ненулевых элементов, что снижает требования к компьютерной памяти. Сложность операции с разреженными матрицами чаще всего определяется не их размером но числом ненулевых элементов. Далее будет показано, что умножение разреженной матрицы на плотный вектор можно произвести ровно за столько умножений сколько в матрице ненулевых элементов.
1.2 Математическое описание алгоритма
Исходные данные: разреженная матрица [math]M^{n*n}[/math], вектор [math]x^n[/math]
Наиболее удобным форматом для вычисления произведения матрицы на вектор является "Compressed Sparse Row" или сокращенно CSR-формат.
Рассмотрим CSR-представление разреженной матрицы: пусть число ненулевых элементов матрицы равно [math]nnz[/math] CSR-формат представляет матрицу [math]M[/math] в виде 3-х одномерных массивов:
массив [math]A[/math] размера [math]nnz[/math] содержит ненулевые значения матрицы, [math]JA[/math] размера [math]nnz[/math] - номера столбцов ненулевых элементов., [math]IA[/math] размера [math]n[/math]- содержит номер с которого начинается описание элементов строки в массивах [math]A[/math] и [math]JA[/math].
Этот формат позволяет производить перемножение матрицы [math]M[/math] на вектор [math]x[/math] за [math]O(nnz)[/math] умножений и сложений. Если при умножении плотной матрицы на вектор каждый элемент результата определяется по формуле [math]y_i = \sum_{k = 1}^{n} A_{ik} x_k[/math], то в случае разреженной матрицы достаточно выполнять умножения только для ненулевых элементов [math]A_ik[/math], которые хранятся в массиве [math]A[/math] в части соответствующей строке [math]i[/math] (элементы с индексами от [math]IA_i[/math] до [math]IA_{i+1}[/math]). Необходимо также знать на какой элемент вектора должен быть домножен данный ненулевой элемент массива, то есть нужен столбцовый индекс каждого элемента [math]A[/math]. Для этого используется массив [math]JA[/math]. Таким образом, каждый элемент итогового вектора определятся формулой
- [math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]
Нетрудно заметить, что общее число операций умножения равно числу элементов [math]A[/math], то есть числу ненулевых элементов разреженной матрицы.
Например, это разреженная матрица с 4-мя ненулевыми элементами
- [math]\begin{pmatrix} 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 1 \\ 0 & 0 & 3 & 0 \\ 0 & 4 & 0 & 0 \\ \end{pmatrix}[/math],
представляемая в формате CSR
A = [ 2 1 3 4 ] IA = [ 0 0 2 3 4 ] JA = [ 0 3 2 1 ]
домножим ее на вектор
x = [ 5 6 7 8 ]
получим
y[0] = 0 y[1] = a[0]*x[0] + a[1]*x[3] = 18 y[2] = a[2]*x[2] = 21 y[3] = a[3]*x[1] = 24
Алгоритм умножения матрицы на вектор полностью детерминирован и не зависит от порядка хранения элементов принадлежащих одной строке.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром алгоритма является формула умножения разреженной матрицы на плотный вектор:
- [math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]
для всех [math]i = 1,n[/math]
1.4 Макроструктура алгоритма
Псевдокод алгоритма:
Входные данные:
число строк матрицы n;
разреженная матрица в формате CSR:
строчные указатели IA,
столбцовые указателиJA,
ненулевые элементы A;
вектор x.
Выходные данные: произведение матрицы на вектор y.
read CSR n, IA, JA, A;
read x
for i = 1,n:
for k = IA(i), IA(i+1)-1:
y(i) += A(k)*x(JA(k));
write y;
1.5 Схема реализации последовательного алгоритма
Метод можно описать следующим образом:
- привести матрицу [math]M[/math] к формату CSR
- для [math]i[/math] от [math]0[/math] до [math]n-1[/math] вычислить [math]y_i[/math] по формуле [math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]
1.6 Последовательная сложность алгоритма
Для вычисления матрично-векторного произведения матрицы размера [math]n*n[/math] и вектора размера n в последовательном варианте требуется:
- [math]nnz[/math] сложений,
- [math]nnz[/math] умножений.
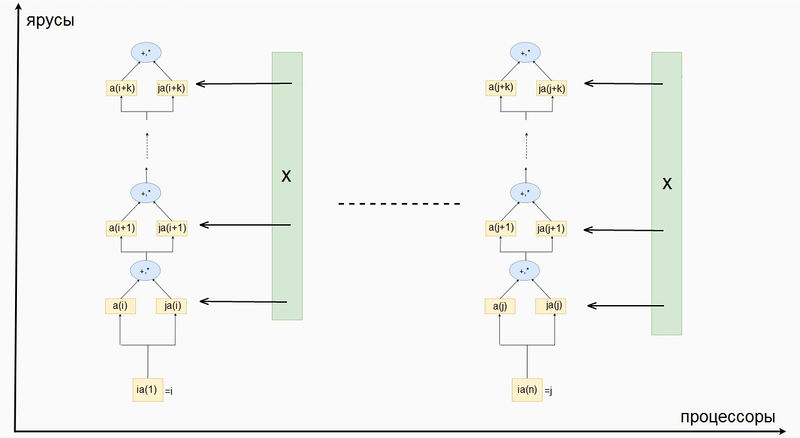
1.7 Информационный граф
Для того чтобы построить информационный граф рассмотрим процесс вычисления значения одного элемента результирующего вектора [math]y_i[/math]. Число последовательных ярусов равно числу последовательных операций -- [math] AI_{i+1} - AI_i [/math] (в данном случае умножение и сложение будем считать за одну операцию). Если же вычисления всех [math]y_i[/math] производить параллельно, на каждом ярусе будет производиться [math]n[/math] операций.
1.8 Ресурс параллелизма алгоритма
Возможность параллельной реализации алгоритма появляется благодаря независимости вычисления каждого элемента результирующего вектора [math]y_i[/math]. Предположим, что имеется неограниченное число процессоров (теоретически, для максимальной эффективности требуется [math]n[/math] процессоров). Каждый процессор работает с одной строкой разреженной матрицы и хранит в памяти только те части массивов [math] AJ [/math] и [math] A [/math], которые соответствуют данной строке. Вектор [math] x [/math] хранится в памяти всех процессоров. Таким образом достигается экономия памяти (объем данных для i-ого процессора [math] 2(AI_{i+1} - AI_i) + n [/math]). На данном процессоре выполняется [math] AI_{i+1} - AI_i [/math] последовательных операций умножения и сложения. Число ярусов для i-ого процессора равно [math] AI_{i+1} - AI_i [/math]. Поскольку изначальная разреженная матрица имеет произвольную структуру, число ярусов на различных процессорах может быть различно. В худшем случае (если в строке все элементы ненулевые) число ярусов будет равно [math]n[/math].
Таким образом, для алгоритма умножения разреженной матрицы на плотный вектор в параллельном варианте требуется последовательно выполнить:
- не более чем [math]n[/math] ярусов умножений и сложений,
- в каждом из ярусов не более чем [math]n[/math] операций.
При классификации по высоте ЯПФ, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.
Замечание: если число процессоров [math]k[/math] меньше числа строк, но отношение [math]\frac{n}{k} = c[/math] является константой, то каждый процессор вычисляет [math]c[/math] элементов результирующего вектора, и число ярусов не более чем [math]cn[/math]. Таким образом, предыдущие оценки сложности сохранятся.
1.9 Входные и выходные данные алгоритма
Входными данными алгоритма являются:
- размер разреженной матрицы [math] n [/math];
- вектор [math] AI [/math] размерности [math] n+1 [/math];
- вектор [math] AJ [/math] размерности [math] nnz [/math];
- вектор [math] A [/math] размерности [math] nnz [/math];
- вектор [math] x [/math] размерности [math] n [/math].
Суммарная размерность входных данных: [math] 2(nnz + n) + 1 [/math]
Выходными данными является
- вектор [math] y [/math] размерности [math] n [/math].
Объем выходных данных: [math] n [/math].
1.10 Свойства алгоритма
Если размерность матрицы [math]n[/math], число ненулевых элементов [math]nnz[/math], для вычисления используется [math]k[/math] процессоров тогда:
- Каждый процессор оперирует с [math]\frac{n}{k}[/math] строками, в каждой из которых примерно [math]\frac{nnz}{n}[/math] элементов. Параллельная сложность алгоритма - [math]O(\frac{nnz}{k})[/math].
- Вычислительная мощность алгоритма (отношение числа операций к суммарному объему входных и выходных данных) - [math]O(\frac{nnz}{2nnz + 3n}) = O(1)[/math] - для последовательного алгоритма; [math]O(\frac{nnz}{n} / (2\frac{nnz}{n} + n)) = O(1) [/math] - для параллельного алгоритма.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Последовательная реализация имеется в пакете SPARSKIT [1], Python.Scipy [2]
Параллельный алгоритм реализован в библиотеке Matlab [3], Intel MKL [4]
3 Литература
[1] С. Писсанецки. Технология разреженных матриц. Изд. Мир, 1988.
[2] В. В. Воеводин, Вл.В. Воеводин. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002.