Участник:Светлана Лукьяненко/Строгий алгоритм С средних (Hard C-Means, HCM)

Строгий алгоритм С средних (Hard C-Means,HCM)
Последовательный алгоритм
Последовательная сложность	[math]O(N)[/math]
Объём входных данных	[math]nN+1[/math]
Объём выходных данных	[math]C(N+n)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(1)[/math]
Ширина ярусно-параллельной формы	[math]O(N)[/math]

Авторы описания: Лукьяненко Светлана(1.1, 1.3, 1.4, 1.8, 1.10, 2.4, 2.7), Комаров Юрий(1.2, 1.5, 1.6, 1.7, 1.8, 1.9, 2.4)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Строгий алгоритм C средних (Hard C-Means; Jang, Sun and Mizutani, 1997) позволяет распределить большие наборы числовых данных по кластерам в многомерном пространстве. Алгоритм является управляемым, так как для работы с ним требуется задание одного параметра — числа кластеров, на которое необходимо разделить данные. Входными данными для алгоритма являются набор векторов и количество кластеров, также может задаваться пороговое значение величины объектной функции, по достижении которого расчёт прекращается. Выходными данными для алгоритма является рядовая матрица, отображающая принадлежность исходных элементов построенным кластерам, и центры построенных кластеров.

Первым шагом выполнения алгоритма является инициализация центров кластеров случайными значениями. Дальнейшие шаги алгоритма выполняются итеративно до тех пор, пока объектная функция не станет меньше порогового значения или же значение объектной функции не будет минимально отличаться от полученного на предыдущей итерации. На каждой итерации вычислений выполняются следующие действия:

1. Расчёт рядовой матрицы, сопоставляющей каждый вектор с ближайшим кластерным центром.
2. Расчёт объектной функции; проверка условий остановки и завершение расчёта в случае их выполнения.
3. Пересчёт кластерных центров.

Так как алгоритм является итеративным и зависит от начальных значений кластерных центров, он может сходиться к локальному минимуму.

1.2 Математическое описание алгоритма

1.2.1 Входные и выходные данные

На вход подаётся набор векторов [math]\{u_k\}_{k=1}^{N}[/math] пространства [math]\mathbb{R}^n[/math] и количество кластеров [math]C[/math].

Конечным результатом работы алгоритма являются построенная рядовая матрица [math]M[/math], содержащая информацию о принадлежности элементов кластерам:

[math] m_{ij} = \begin{cases} 1, & u_j \in C_i, \\ 0, & \text{otherwise}, \end{cases} [/math]

где под [math]C_i[/math] подразумевается [math]i[/math]-ый построенный кластер, и набор [math]\{c_i\}_{i=1}^{C}[/math] центров этих кластеров.

1.2.2 Описание алгоритма

Алгоритм состоит из 5 последовательных шагов.

Шаг 1

Инициализация кластерных центров [math]c_i \, (i=1,2,\ldots,C)[/math] может происходить за счёт случайного выбора необходимого числа точек из входного набора либо путём явного указания.

Шаг 2

Вычисление рядовой матрицы [math]M = \|m_{ik}\|[/math], элементы которой задаются следующими выражениями ([math]N[/math] — количество элементов во входном наборе данных):

[math] m_{ik} = \begin{cases} 1, & \|u_k-c_i\|^2 \leqslant \|u_k-c_j\|^2 \;\; \text{for all } i \neq j; \;\; (i,j=1,2,\ldots,C; \; k = 1,2,\ldots,N)\\ 0, & \text{otherwise}. \end{cases} [/math]

Будем говорить, что [math]u_k \in C_i[/math], если [math]m_{ik} = 1[/math].

Шаг 3

Расчёт объектной функции:

[math] J = \sum\limits_{i=1}^C J_i = \sum\limits_{i=1}^C \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right) .[/math]

На этом шаге происходит остановка и выход из цикла, если полученное значение ниже пороговой величины [math]\varepsilon_{tr}[/math] или полученное значение не сильно отличается от значений, полученных на предыдущих циклах.

Шаг 4

Пересчёт кластерных центров выполняется в соответствии со следующим уравнением:

[math] c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k, [/math]

где под [math]|C_i|[/math] подразумевается количество элементов в [math]i[/math]-ом кластере.

Шаг 5

Переход по циклу на шаг 2.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляют вычисления квадратов нормы расстояния от каждого из векторов исходной выборки до промежуточных кластерных центров [math]\|u_k-c_i\|^2[/math]. На каждой итерации алгоритма происходит расчёт [math]CN[/math] таких расстояний.

1.4 Макроструктура алгоритма

Основной операцией, выполняемой в алгоритме, как сказано выше, является операция нахождения квадратов расстояний между исходными векторами и кластерными центрами.

[math] d_{ki} = \|u_k-c_i\|^2 [/math]

Также на шаге вычисления объектной функции производится множественное суммирование полученных расстояний:

[math] J = \sum\limits_{i=1}^C J_i = \sum\limits_{i=1}^C \left( \sum\limits_{k:\, u_k \in C_i} \|u_k -c_i \|^2 \right), [/math]

а на шаге расчета кластерных центров происходит суммирование векторов:

[math] c_i = \frac{1}{|C_i|} \sum\limits_{k:\, u_k \in C_i} u_k. [/math]

1.5 Схема реализации последовательного алгоритма

Реализация последовательного алгоритма состоит в итеративном повторении блока, описанного далее в форме псевдокода, до тех пор, пока не будет достигнута желаемая точность.

J = 0;
M = zeros(N,C);
for i = 1 to N //go through every element
   d_min = MAXINT;
   j_min = 1;
   for j = 1 to C //deside which claster does element belong to
      d_ij  = sq_norm(u[i] - c[j]);
      if d_ij < d_min
         d_min = d_ij;
         j_min = j;
   //generation of output data
   J += d_min; 
   M[i,j_min] = 1;
   c_new[j] += u[i];
   c_newCount[k]++;

1.6 Последовательная сложность алгоритма

На каждой итерации алгоритма требуется выполнение:

• [math]NC[/math] операций вычисления квадрата нормы разности элементов;
• [math]NC[/math] операций сравнения (вычитаний);
• [math]3N[/math] операций сложения.

Каждая операция вычисления нормы разности векторов предполагает выполнение [math]2n-1[/math] арифметических операций сложения и вычитания и [math]n[/math] операций возведения в квадрат (умножений), поэтому получаем для каждой итерации:

• [math](2nC + 3)N[/math] арифметических операций сложения и вычитания;
• [math]nNC[/math] операций умножения.

Ожидая, что предельная точность будет достигнута менее, чем за [math]N[/math] итераций (в противном случае применение алгоритма можно считать нецелесообразным), получаем итоговую сложность последовательной реализации алгоритма [math]O(N)[/math] (в предположении, что [math]n[/math] и [math]C[/math] существенно меньше [math]N[/math]).

1.7 Информационный граф

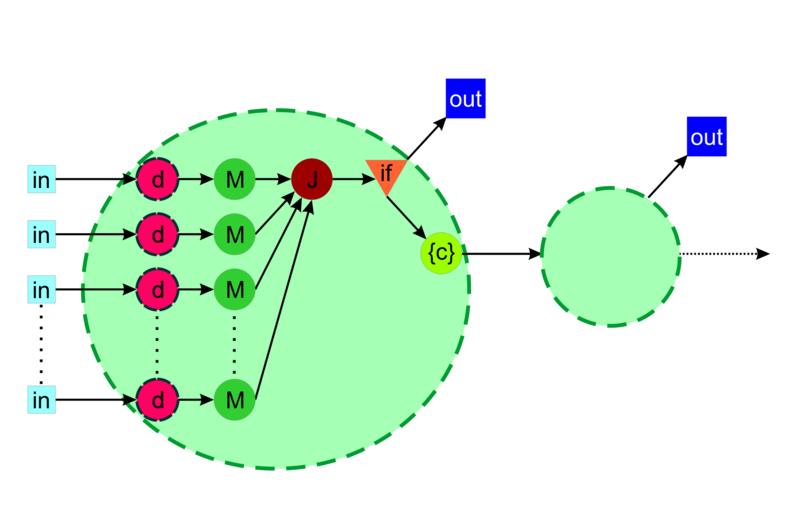
Приведём аналитическое и графическое описание графа алгоритма.

Граф алгоритма состоит из 5 различных видов вершин.

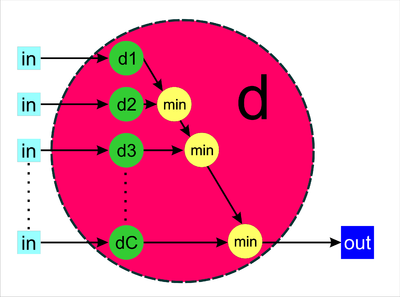
Первая группа вершин отмечена символом d, ей соответствует вычисление минимального расстояния до кластерных центров, включающее в себя следующую последовательность действий:

• независимое вычисление расстояний от заданного элемента [math]u_i[/math] до каждого из кластерных центров;
• последовательное сравнение полученных значений с целью отыскания минимума;
• передача найденного минимального расстояния и соответствующего ему индекса кластера.

Вторая группа вершин отмечена символом M, ей соответствует операция записи единички в столбец, отвечающий текущей ветке графа, в позицию, полученную на предыдущем шаге и соответствующую ближайшему кластерному центру.

Третья вершина отмечена символом J, подразумевается, что на этом этапе происходит расчёт объектной функции.

Четвертая вершина обозначена треугольным маркером и помечена if, на этом этапе происходит проверка условия достижения необходимой точности (условия остановки итерационного процесса).

Пятая соответствует операции пересчёта кластерных центров, она отмечена как {c}.

Все эти виды вершин визуально выделены в одну большую группу, поскольку все вместе они составляют одну полную итерацию алгоритма.

Рисунок 1. Информационный граф алгоритма. Здесь in — ввод входных данных ([math]C[/math] стартовых значений кластерных центров и 1 значение [math]u_i[/math] на каждую вершину графа), d — вычисление минимального расстояния до кластерных центров (подробнее см. рисунок 2), M — запись единички в соответствующий столбец матрицы [math]M[/math], J — вычисление объектной функции по результатам полученных вычислений, if — проверка условия достижения заданной точности, {c} — пересчёт кластерных центров и out — вывод полученных данных (матрица [math]M[/math] и [math]C[/math] значений полученных кластерных центров).

Рисунок 2. Подробное описание работы блока d. Здесь in — ввод входных данных (по 1 значению центра кластера на каждую из [math]C[/math] соответствующих вершин графа и значение [math]u_i[/math], единое для этого d-блока), d1,...,dC — прямое вычисление расстояния до кластерных центров, min — вычисление минимума двух чисел (с сохранением соответствующего минимуму кластерного индекса) и out — вывод полученных данных (индекс кластерного центра, расположенного ближе всего к точке [math]u_i[/math], и соответствующее расстояние).

1.8 Ресурс параллелизма алгоритма

Для выполнения одной итерации алгоритма C средних необходимо выполнить параллельно ряд вычислений для каждого из [math]N[/math] элементов:

1. Вычисление [math]C[/math] расстояний между элементом и кластерными центрами.
2. Выполнение [math](C - 1)[/math] сравнений для определения минимального.
3. Определение значений соответствующего рассматриваемому элементу [math]u_i[/math] столбца матрицы [math]M[/math].

Эта последовательность операций может быть выполнена для каждого элемента [math]u_i[/math] входной выборки независимо и поэтому составляет основной ресурс параллелизма алгоритма.

При этом, как можно видеть из информационного графа алгоритма, часть вычислений проводится в последовательном режиме, например, расчёт значения объектной функции [math]J[/math]. Аналогичная ситуация имеет место и с пересчётом кластерных центров — разделив эту операцию на [math]C[/math] независимых процессов, мы потеряем в производительности за счёт увеличения накладных расходов, связанных с пересылкой данных и координацией вычислений.

Стоит отметить, что при малом объёме выборки и размерности системы попытка использования параллельной реализации алгоритма приведёт к понижению производительности, поскольку проведение последовательных расчётов потребует меньше времени, нежели пересылка данных (хотя бы матриц размера [math]nC[/math], определяющих кластерные центры).

При этом, как легко видеть, ширина ЯПФ составляет [math]O(N)[/math] (если быть точнее, просто [math]N[/math]). Высота ЯПФ для строгого алгоритма C средних оценивается как [math]O(1)[/math] (предполагаем, что число итераций существенно меньше объёма выборки [math]N[/math]).

1.9 Входные и выходные данные алгоритма

Входные данные:

• [math]\{u_k\}_{k=1}^{N} \subset \mathbb{R}^n[/math] — исходный набор векторов;
• [math]C[/math] — количество кластеров ([math]2 \leqslant C \leqslant N[/math]);
• (опционально) [math]\varepsilon_{tr}[/math] — пороговая точность работы алгоритма.

Объём входных данных: [math]nN+1[/math].

Выходные данные:

• [math]M[/math] — рядовая матрица из пространства [math]\mathbb{R}^{C \times N}[/math].
• [math]\{c_k\}_{k=1}^{C}[/math] — набор построенных кластерных центров.

Объём выходных данных: [math]C(N+n)[/math].

1.10 Свойства алгоритма

Назначение: кластеризация больших наборов числовых данных.

Достоинства:

• лёгкость реализации;
• вычислительная простота.

Недостатки:

• нет гарантии, что итерационный процесс сойдётся к оптимальному решению;
• производительность существенно зависит от выбора начальных кластерных центров.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

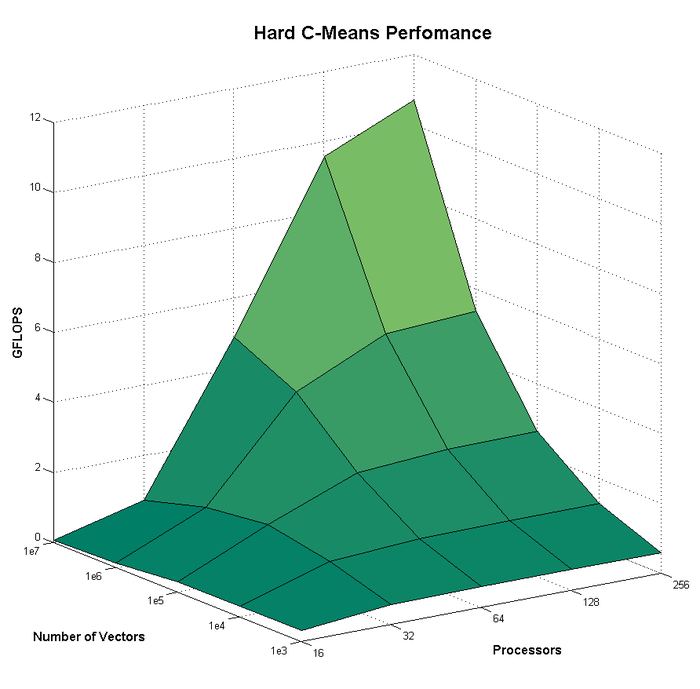
Исследуем масштабируемость параллельной реализации строгого алгоритма C средних, соответствующей последовательной реализации, описанной в п1.5. Для проведения расчётов использовались ресурсы вычислительного комплекса IBM Blue Gene/P и собственная реализация алгоритма, поскольку в открытом доступе параллельные реализации алгоритма авторами найдены не были (п2.7).

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [math][16 : 256][/math] с шагом по степеням двойки;
• объём выборки [math][10^3:10^7][/math] с шагом по степеням десятки;
• размерность системы [math]n=10[/math];
• количество кластеров [math]C = 11[/math].

В качестве изменяемого параметра для построения графика был выбран объём выборки [math]N[/math], поскольку варьирование прочих параметров существенно хуже отражает возможности применения технологии параллельных вычислений. Это связано с тем, что при малом количестве векторов время, затраченное на пересылку данных, сравнимо со временем, затрачиваемым непосредственно на расчёты; это хорошо видно на графике: при объёмах выборки, составляющих [math]10^3[/math] и [math]10^4[/math] векторов, использование большего числа процессоров не приводит к приросту производительности (наоборот, производительность падает) ввиду высоких накладных расходов.

Рис.3 Реализация строгого алгоритма C средних. График производительности (GFLOPS) в зависимости от числа параллельных процессов и объёма выборки.

2.7 Существующие реализации алгоритма

1) Последовательная реализация на С++

2) Последовательная реализация на MatLab

На момент публикации параллельных реализаций в свободном доступе обнаружено не было.