Участник:Anlesnichiy/Решение задачи Коши для системы ОДУ методом Рунге-Кутты 4 порядка

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 14.10.2016 Авторы этой статьи считают, что задание выполнено.

Решение задачи Коши для системы ОДУ методом Рунге-Кутты 4 порядка
Последовательный алгоритм
Последовательная сложность	[math] 4mn [/math]
Объём входных данных	[math] m + 3 [/math]
Объём выходных данных	[math] (m+1)n [/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] O(n) [/math]
Ширина ярусно-параллельной формы	[math] O(m) [/math]

Основные авторы описания: А.А. Лесничий(1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9), Д.А. Алимов(1.1,1.7,1.10,2.4,2.7)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Рунге-Кутты четвертого порядка — наиболее распространенный метод из семейства методов Метод Рунге-Кутты численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения.
Основная идея алгоритмов Рунге - Кутты состоит в замене правой части дифференциального уравнения, зависящей от искомой неизвестной функции, некоторым приближением. Если задачу Коши переписать в интегральном виде

[math] y(x) = y_{0} + \int\limits_{x_{0}}^{x}f(t,y)dt, [/math]

то, применяя различные численные формулы для расчёта интеграла в правой части уравнения, можно получить методы Рунге - Кутты различных порядков.

Общий вид формул методов Рунге - Кутты с шагом сетки [math]h_{n}[/math]:

[math] y = f(t,y),\,\,\, y(t_{0}) = y_{0}, [/math]

[math] y_{n+1} = y_{n} + h_{n+1}\sum\limits_{i=1}^{s}b_{i}K_{n}^{i}, [/math]

где

[math] K_{n}^{i} = f(t_{n} + c_{i}h_{n+1}, y_{n} + h_{n+1}\sum\limits_{j=1}^{i-1}a_{ij}K_{n}^{j}). [/math]

Конкретный метод Рунге - Кутты определяется набором коэффициентов [math]b_{i}, c_{j}, a_{ij}[/math], которые должны удовлетворять определённым соотношениям.

1.2 Математическое описание алгоритма

1.2.1 Метод Рунге-Кутты 4-го порядка для задачи Коши для ДУ первого порядка

Рассмотрим задачу Коши, где правая часть удовлетворяет условиям теорем существования и единственности решения.

[math] y' = f(x,y),\ a \leq x \leq b;\ y(a) = y^0 [/math]

Зададим равномерную сетку

[math] x_i = a + ih,\ i = 1,\dots, n,\ h = \frac{b-a}{n} [/math]

Введём обозначения [math]y(x_i) = y_i[/math]. Получим вычислительную формулу:

[math] \begin{cases} k_1 = hf(x_i,y_i)\\ k_2 = hf(x_i + h/2,y_i + k_1/2)\\ k_3 = hf(x_i + h/2,y_i + k_2/2)\\ k_4 = hf(x_i + h,y_i + k_3)\\ y_{i+1} = y_i + [ k_1 + 2k_2 + 2k_3 + k_4 ]/6 \\ \end{cases} [/math]

1.2.2 Метод Рунге-Кутты 4-го порядка для задачи Коши для системы ДУ первого порядка

Численное решение задачи Коши для систем ОДУ 1-го порядка методами Рунге-Кутты ищется по тем же формулам, что и для ОДУ первого порядка. Например, решение методом Рунге-Кутты 4-го порядка можно найти, если положить:

[math] y_i \rightarrow \bar y_i [/math]

[math] f(x_i,y_i) \rightarrow \bar f(x_i,\bar y_i) [/math]

[math] k_l \rightarrow \bar k_l [/math]

[math] \bar k_l = \begin{pmatrix} k^i_{l,1}\\ \vdots\\ k^i_{l,m}\\ \end{pmatrix} [/math]

где m – размерность системы, [math] l = 1, \dots, 4 [/math]. В результате получим

[math] \begin{cases} \bar k_1 = h\bar f(x_i,\bar y_i)\\ \bar k_2 = h\bar f(x_i + h/2,\bar y_i + \bar k_1/2)\\ \bar k_3 = h\bar f(x_i + h/2,\bar y_i + \bar k_2/2)\\ \bar k_4 = h\bar f(x_i + h,\bar y_i + \bar k_3)\\ \bar y_{i+1} = \bar y_i + [ \bar k_1 + 2\bar k_2 + 2\bar k_3 + \bar k_4 ]/6 \\ \end{cases} [/math]

1.3 Вычислительное ядро алгоритма

Вычислительным яром алгоритма можно считать вычисление значение вектора [math] \bar y_i [/math], то есть вычислительным ядром является цикл по i. Иными словами сам алгоритм совпадает со своим ядром и был описан в пункте 1.2.2.

1.4 Макроструктура алгоритма

Макроструктуру алгоритма составляют вычисления коэффициентов [math]k_{j},\,j=1,..,4[/math] при нахождении значений искомой функции в каждом узле.

1.5 Схема реализации последовательного алгоритма

Приведем возможную реализацию последовательного алгоритма на языке Matlab (правая часть ОДУ задана в виде функции func(x,y))

 1  function [x, y] = RungeKutta4(y0, a, b, n)
 2      h = (b-a)/n;
 3      x = a : h : b
 4 
 5      y(:, 1) = y0;
 6      for i = 2 : n
 7          k1        = h*func(x(i), y(:, i))
 8          k2        = h*func(x(i) + h/2, y(:, i) + k1/2)
 9          k3        = h*func(x(i) + h/2, y(:, i) + k2/2)
10          k4        = h*func(x(i) + h, y(:, i) + k3)
11          y(:, i+1) = y(:, i) + (k1 + 2*k2 + 2*k3 + k4)/6 
12      end
13  end

1.6 Последовательная сложность алгоритма

Каждый шаг цикла алгоритма состоит из 4 обращений к функции [math] \bar f [/math], 11 умножений и 10 сложений. Так как обращение к функции [math] \bar f [/math] является наиболее сложной операцией, то сложность линейного выполнения алгоритма можно определить как [math] 4mn [/math].

1.7 Информационный граф

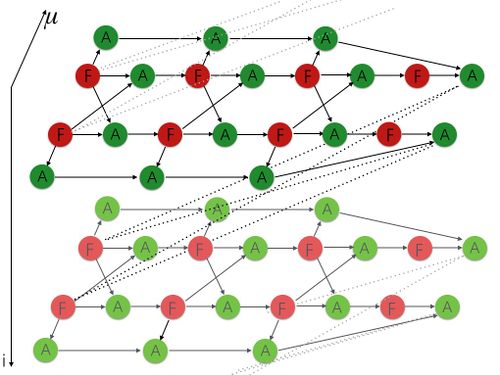
Опишем граф алгоритма аналитически и графически.
Пусть задана система из [math] m [/math] одномерных дифференциальных уравнений. Граф имеет трёхмерную структуру, которая представляет собой связанные между собой ограниченные плоскости (уровни). На каждом i-ом уровне вычисляется i-ое приближение вектора решения системы. Всего таких уровней – n, где n – количество узлов, в которых вычисляется приближённое решение системы дифференциальных уравнений. Выходные данные i-го уровня являются входными данными для i+1-го уровня.
Вершины информационного графа делятся на два типа:

• Первому типу вершин соответствует вычисление одной координаты функции, стоящей в правой части дифференциального уравнения, в точках, подаваемых на вход вершине. Результатом выполнения операции является одна координата вектора [math]k_{l},\,\,\,l = 1,2,3,4[/math]. На каждом уровне таких вершин будет [math]4m[/math], а их общее количество – [math]4mn[/math].
• Второму типу вершин соответствует операция [math]a + bc[/math]. Эти вершины также можно разделить на две группы. В вершинах первой группы вычисляются выражения, результат которых будет подаваться в качестве аргументов для вершин первого типа, при этом входными данными для этих вершин будут результаты срабатывания m вершин первого типа, расположенных на одном уровне. На каждом уровне вершин первой группы будет [math]3m[/math], а их общее количество – [math]3mn[/math]. Входными данными для вершин второй группы будет результат срабатывания одной вершины первого типа и одной такой же вершины второго типа. Результатом срабатывания данной вершины на i-ом уровне будут m координат вектора i-го приближения решения системы. На каждом уровне таких вершин будет [math]4m[/math], а их общее количество – [math]4mn[/math].

Приведём графическую иллюстрацию информационного графа. Для того чтобы сильно не загромождать граф, рассмотрим случай системы из двух дифференциальных уравнений. Красным цветом обозначены вершины первого типа, зелёным - вершины второго типа. Входные данные задачи подаются на все вершины первого типа, а также на [math]m[/math] левых вершин второй группы второго типа и на все вершины первой группы второго типа на первом уровне подаются начальные значения искомой функции (см. пункт 1.8). Выходными данными будут результаты срабатывания [math]m[/math] правых вершин второй группы второго типа на каждом уровне. Результаты срабатывания остальных вершин являются промежуточными данными алгоритма.

Информационный граф для системы из двух дифференциальных уравнений

1.8 Ресурс параллелизма алгоритма

Поскольку в описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) [/math], то основное внимание следует уделить распараллеливанию этой операции. Здесь будет применяться подход декомпозиции уравнений системы ОДУ на подсистемы. Поэтому для инициализации рассмотрим следующую схему декомпозиции данных по имеющимся процессорным элементам с локальной памятью: на каждый [math]\mu[/math]- ПЭ (процессорный элемент) ([math]\mu = 0, \dots, p-1 [/math]) распределяется [math] n/p [/math] дифференциальных уравнений и вектор [math] \bar y_0 [/math]. Далее расчеты производятся по следующей схеме:

1. на каждом ПЭ одновременно вычисляются [math] n/p [/math] соответствующих компонент вектора [math] \bar k_1 [/math] по формуле [math] [ \bar k_1 ]_{\mu} = h[ \bar f(x_i, \bar y_i) ]_{\mu} [/math]
2. для обеспечения второго расчетного этапа необходимо провести сборку вектора [math] \bar k_1 [/math] целиком на каждом ПЭ. Затем независимо выполняется вычисление компонент вектора [math] \bar k_2 [/math] по формуле [math] [ \bar k_2 ]_{\mu} = h[ \bar f(x_i + h/2,\bar y_i + \bar k_1/2)]_{\mu} [/math];
3. проводится сборка вектора [math] \bar k_2 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_3:\ [ \bar k_3 ]_{\mu} = h [\bar f(x_i + h/2,\bar y_i + \bar k_2/2)]_{\mu} [/math];
4. проводится сборка вектора [math] \bar k_3 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_4:\ [ \bar k_4 ]_{\mu} = h [\bar f(x_i + h,\bar y_i + \bar k_3)]_{\mu} [/math];
5. рассчитываются с идеальным параллелизмом компоненты вектора [math] \bar y_{i+1}:\ [\bar y_{i+1}]_{\mu} = [\bar y_{i}]_{\mu} + ([ \bar k_1 ]_{\mu} + 2[ \bar k_2 ]_{\mu} + 2[ \bar k_3 ]_{\mu} + [ \bar k_4 ]_{\mu})/6\ [/math] и производится сборка вектора [math] \bar y_{i+1} [/math] на каждом ПЭ. Если необходимо продолжить вычислительный процесс, то полагается [math] i = i + 1 [/math] и осуществляется переход на п. 1

Заметим, что данный алгоритм обладает конечным параллелизмом, но не массовым, так как циклы алгоритма являются информационно зависимыми.

На каждом ярусе в данном алгоритме каждый ПЭ производит четыре операции вычисления правых частей ОДУ, шестнадцать операций сложения векторов и умножения вектора на число, а так же р-1 пересылку данных между другими ПЭ, что довольно сильно замедляет выполнение алгоритма и является накладными расходами при распараллеливании алгоритма. При этом количество итераций цикла равно длине вектора [math] x [/math], то есть [math] n [/math]. Из вышеуказанного следует, что при классификации по высоте ЯПФ алгоритм имеет сложность [math] O(n) [/math], а при классификации по ширине ЯПФ – O(m) (при условии, что [math] p = m [/math]).

1.9 Входные и выходные данные алгоритма

Входными данными алгоритма являются:

1. вектор [math] y^0 [/math] размерности [math] m [/math];
2. границы временного интервала [math] a [/math] и [math] b [/math];
3. частота дискретизации [math] n [/math];

Всего размер входных данных: [math] m + 3 [/math]

Выходными данными являются

1. [math] n [/math] векторов [math] \bar y_i [/math] размерности [math] m [/math];
2. вектор [math] \bar x [/math] размерности [math] n [/math]

Всего размер выходных данных: [math] (m+1)n [/math]

1.10 Свойства алгоритма

Перечислим основные свойства алгоритма:

• Точность. Как следует из названия, у метода Рунге-Кутты 4-го порядка ошибка на конечно интервале интегрирования имеет порядок [math]\mathcal{O}(h^{4})[/math], где [math]h[/math] – расстояние между узлами, в которых вычисляется искомая функция.
• Устойчивость. Метод имеет интервал абсолютной устойчивости [math](-2.78; 0)[/math]. (Определение понятия интервала абсолютной устойчивости см. [2])
• Отношение числа расчётов функции, стоящей в правой части задачи Коши, при последовательном алгоритме к числу расчётов при параллельном равняется [math]p[/math], где [math]p[/math] число, используемых процессорных элементов. То есть при увеличении числа используемых процессорных элементов скорость расчётов увеличивается, но стоит учитывать, что число пересылок данных между процессами при этом резко увеличивается также и, в свою очередь, замедляет работу программы.
• Если известен класс функций, которые могут стоять в правой части задачи Коши, то алгоритм можно эффективно модифицировать, чтобы избавиться от лишних пересылок данных.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

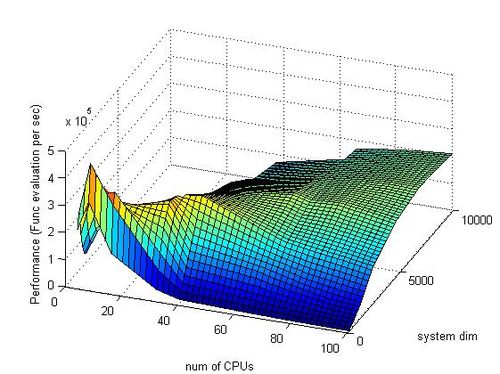
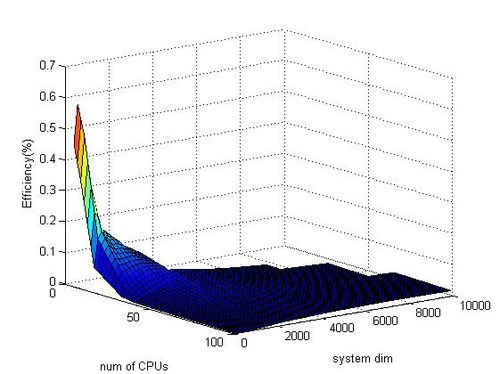
Раздел не закончен.

Минимальная эффективность реализации 0.00032%;

Максимальная эффективность реализации 0.54%;

Изменение производительности параллельного алгоритма в зависимости от размерности системы

Эффекивность работы параллельного алгоритма в зависимости от размерности системы

Построим оценки масштабируемости метода Рунге - Кутты 4-го порядка:

1. По числу процессоров -0.0000417;

2. По размеру задачи 0.00000526;

3. По двум направлениям -0.000000027;

2.7 Существующие реализации алгоритма

Метод 4-го порядка является самым часто используемым из всех схем Рунге - Кутты, поэтому существует множество его программных последовательных реализаций как коммерческих, так и бесплатных. Одной из самых известных программных реализаций является ode45 в среде MATLAB, у которой имеется большое количество возможностей для настройки численного расчёта, что делает её достаточно удобной для использования. Также метод Рунге - Кутты 4-го порядка реализован в параллельной библиотеке PETSc, которая является свободно распространяемой. Несмотря на то, что в этой библиотеки большинство методов реализовано с использованием параллельных алгоритмов, метод Рунге - Кутта в ней реализован последовательным. Довольно трудно найти параллельную реализацию метода в случае рассмотрения общей задачи Коши, но существует множество научных работ, в которых описываются параллельные реализации метода Рунге - Кутты для конкретных классов систем, например, в [1] описывается параллельная реализация для линейных систем.

3 Литература

[1] А. В. Старченко, В. Н. Берцун. Методы параллельных вычислений - Издательство Томского университета, 2013 - 173 с.

[2] А. Ф. Заусаев. Разностные методы решения обыкновенных дифференциальных уравнений. Учебное пособие. Самарский гос. техн. ун-т, 2010 - 100 с. <references \>