Плотностный алгоритм кластеризации DBSCAN
Последовательный алгоритм
Последовательная сложность	[math]-[/math]
Объём входных данных	[math]-[/math]
Объём выходных данных	[math]-[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]-[/math]
Ширина ярусно-параллельной формы	[math]-[/math]

Авторы описания: Вашуров И.М., Шемякин Р.О.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Задача кластеризации - это задача разбиения заданной входной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Алгоритм DBSCAN (Density-based spatial clustering of applications with noise)^[1] был предложен Мартином Эстер, Гансом-Питером Кригель и коллегами в 1996 году как решение задачи кластеризации с кластерами произвольной формы. DBSCAN является непараметрическим плотностным алгоритмом кластеризации: для заданного набора точек в некотором пространстве, алгоритм группирует те точки, которые расположены достаточно близко друг к другу (точки с большим количеством соседей), и помечает как выбросы те, что располагаются далеко от ближайших соседей.

Близость в алгоритме определяется заданной в пространстве метрикой. Наиболее часто в качестве метрики используются Евклидово расстояние, квадрат Евклидова расстояния, манхэттенская метрика, расстояние Чебышева или степенное расстояние.

1.2 Математическое описание алгоритма

Вход алгоритма: множество точек [math]X[/math] из [math]n[/math]-мерного пространства, на котором определена функция расстояния [math]D[/math].

Выход алгоритма: размеченное множество точек [math]X[/math], в котором каждой точке соответствует номер ее кластера.

Параметры алгоритма:

[math]\varepsilon[/math] - максимальное расстояние между соседями;
[math]MinPts[/math] - минимальное количество соседей для создания области связности.

1.2.1 Определения

Рис. 1. Здесь MinPts = 4. Точка A и другие красные точки - ядровые и образуют единый кластер, так как достижимы друг из друга. Точки B и C не являются ядровыми, но достижимы из A, а значит также принадлежат кластеру. Точка N - не достижима из других точек и является шумом.

Все заданные точки классифицируются на три группы:

ядровые точки: точка [math]p[/math] является ядровой, если количество [math]\varepsilon[/math]-соседей, включая саму точку [math]p[/math], не меньше [math]MinPts[/math]. Под [math]\varepsilon[/math]-соседями точки [math]p \in X[/math] понимается множество точек, расстояние до которых не превышает [math]\varepsilon[/math], т.е. [math]N_\varepsilon(p) = \{ x \in X | D(p, x) \le \varepsilon \}[/math]. Эти точки являются напрямую достижимыми из [math]p[/math];

достижимые точки: точка [math]q[/math] достижима из [math]p[/math], если существует путь [math]p_1, \dots, p_n[/math], где [math]p_1 = p[/math] и [math]p_n = q[/math], для которого выполнено:

[math]\begin{align} p_{i + 1} \in N_\varepsilon(p_i), i = 1, \dots, n-1 \\ | N_\varepsilon(p_{i}) | \ge MinPts, i = 1, \dots, n-1 \\ \end{align}[/math]

шум (выбросы): все точки, недостижимые из какой-либо другой точки считаются шумом (выбросом).

Так, если [math]p[/math] - ядровая точка, то она образует кластер вместе со всеми точками, достижимыми из неё. Каждый кластер содержит по крайней мере одну ядровую точку; неядровые точки могут быть частью кластера, образуя при этом его "границу", так как они не могут быть использованы для достижения других точек.

Достижимость не является симметричным отношением, так как по определению никакая точка не может быть достижима из неядровой точки, независимо от расстояния. Поэтому в DBSCAN применяется следующий термин связности: две точки [math]p[/math] и [math]q[/math] связанны, если существует такая точка [math]o[/math], что [math]p[/math] и [math]q[/math] достижимы из [math]o[/math]. Такое отношение связности симметрично.

Кластер в таком случае определяется двумя свойствами:

Все точки внутри кластера взаимно связанны;
Если точка достижима из любой точки кластера, она также является частью кластера.

1.2.2 Шаги алгоритма

Выбирается произвольная непосещенная точка [math]p[/math].
Точка [math]p[/math] помечается как посещенная.
У точки [math]p[/math] определяется множество её [math]\varepsilon[/math]-соседей - [math]N_\varepsilon(p)[/math].
- Если точка [math]p[/math] оказалась ядровой - [math]| N_\varepsilon(p) | \ \ge MinPts[/math], то:
  - она становится началом нового кластера или сохраняет номер кластера, который был ей присвоен ранее;
  - все точки из [math]N_\varepsilon(p)[/math] добавляются в её кластер;
  - процесс продолжается рекурсивно для каждой новой добавленной непосещенной точки [math]p' \in N_\varepsilon(p)[/math] c шага 2 (в качестве новой [math]p[/math]).
- Если точка [math]p[/math] оказалась не ядровой, то [math]p[/math] объявляется шумом. Алгоритм продолжается с шага 4.
Если остались непосещенные точки, то алгоритм продолжается с шага 1.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является нахождение [math]\varepsilon[/math]-соседей каждой точки входного множества [math]X[/math].

Для решения этой задачи требуется найти расстояния между любыми двумя точками множества [math]X[/math] по заданной метрике.

1.4 Макроструктура алгоритма

Как записано и в описании ядра алгоритма, основную часть метода составляют вызовы функции [math]request\_neighbours[/math] получения [math]\varepsilon[/math]-соседей и нахождение расстояний между точками множества [math]X[/math].

1.5 Схема реализации последовательного алгоритма

[math]DBSCAN(X, \varepsilon, MinPts)[/math]
  [math]C = 0[/math]
  for [math]\forall p \in X[/math]
     if [math]p[/math] is visited then
        continue
     mark [math]p[/math] as visited
     [math]neighbours[/math] = [math]request\_neighbours(p, \varepsilon)[/math]
     if [math]| neighbours | \lt  MinPts[/math] then
        mark [math]p[/math] as [math]NOISE[/math]
     else
        [math]C = next\_cluster[/math]
        [math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math]

[math]expand\_cluster(p, neighbours, C, \varepsilon, MinPts)[/math]
  add [math]p[/math] to cluster [math]C[/math]
  for [math]\forall p' \in neighbours[/math]
     if [math]p'[/math] is not visited 
        mark [math]p'[/math] as visited
        [math]neighbours'[/math] = [math]request\_neighbours(p, \varepsilon)[/math]
        if [math]| neighbours' | \ \ge MinPts[/math]
           [math]neighbours[/math] = [math]neighbours \cup neighbours'[/math]  
     if [math]p'[/math] is not yet member of any cluster
        add [math]p'[/math] to cluster [math]C[/math]

 [math]request\_neighbours(p, \varepsilon)[/math]
  return [math]\{ p' \ | \ \forall p' \in X: D(p, p') \lt  \varepsilon \}[/math]

1.6 Последовательная сложность алгоритма

DBSCAN проходит через каждую точку входного множества, возможно, по несколько раз. Временная сложность зависит в большей степени от вызова функции [math]request\_neighbours[/math] (нахождение [math]\varepsilon[/math]-соседей для заданной точки). Эта функция вызывается ровно один раз для каждой точки множества [math]X[/math].

Если использовать индексированную структуру данных (например, R-деревья), выполяющую операцию [math]request\_neighbours[/math] за [math]O(\log n)[/math], то суммарная сложность алгоритма в среднем составит [math]O(n \log n)[/math], с учётом хорошо подобранного параметра [math]\varepsilon[/math], такого что в среднем [math]request\_neighbours[/math] возвращает [math]O(\log n)[/math] точек. Без использования ускоряющих структур или на вырожденных данных (таких, что все точки находятся на расстоянии меньшем, чем [math]\varepsilon[/math] друг от друга) сложность по времени в худшем случае будет [math]O(n^2)[/math].

Расстояния между точками можно вычислить заранее за [math]O(\frac {n(n - 1)}{2})[/math], например в виде матрицы расстояний, но это потребует [math]O(n^2)[/math] памяти. Иначе, расстояния будут вычисляться при каждом запуске функции [math]request\_neighbours[/math] за [math]O(n)[/math] и потребуют [math]O(n)[/math] памяти. Итоговая сложность вычисления расстояний в таком случае составляет [math]O(n^2)[/math]. Сложность рассчета расстояний зависит от природы объектов из [math]X[/math] и заданной метрики [math]D[/math]. Например, если [math]X\subset\mathbb{R}^m[/math], то сложность равна [math]O(m)[/math], но оценка может быть улучшена при использовании векторных операций.

1.7 Информационный граф

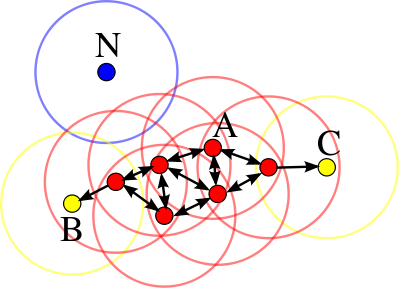
Опишем граф алгоритма^[2]^[3]^[4].

>>> Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций [1].

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

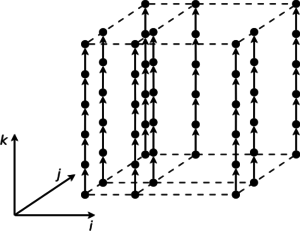
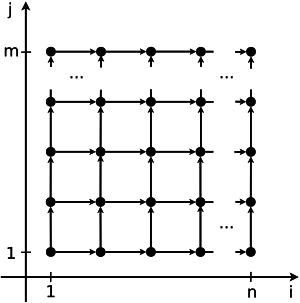
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

<<<

1.8 Ресурс параллелизма алгоритма

Поиск [math]\varepsilon[/math]-соседей требует вычисления [math]n[/math] расстояний (функция [math]D[/math]) и выполнения [math]n[/math] сравнений с [math]\varepsilon[/math]. Эти операции для каждой пары точек независимы и могут быть выполнены параллельно. Таким образом, при наличии неограниченного числа процессоров сложность поиска составит [math]O(1)[/math]. Т.к. поиск выполняется для каждой точки ровно один раз, параллельная сложность всего алгоритма составит [math]O(n)[/math].

>> Здесь приводится оценка параллельной сложности алгоритма: числа шагов, за которое можно выполнить данный алгоритм в предположении доступности неограниченного числа необходимых процессоров (функциональных устройств, вычислительных узлов, ядер и т.п.). Параллельная сложность алгоритма понимается как высота канонической ярусно-параллельной формы [1]. Необходимо указать, в терминах каких операций дается оценка. Необходимо описать сбалансированность параллельных шагов по числу и типу операций, что определяется шириной ярусов канонической ярусно-параллельной формы и составом операций на ярусах.

Параллелизм в алгоритме часто имеет естественную иерархическую структуру. Этот факт очень полезен на практике, и его необходимо отразить в описании. Как правило, подобная иерархическая структура параллелизма хорошо отражается в последовательной реализации алгоритма через циклический профиль результирующей программы (конечно же, с учетом графа вызовов), поэтому циклический профиль (п.1.5) вполне может быть использован и для отражения ресурса параллелизма.

Для описания ресурса параллелизма алгоритма (ресурса параллелизма информационного графа) необходимо указать ключевые параллельные ветви в терминах конечного и массового параллелизма. Далеко не всегда ресурс параллелизма выражается просто, например, через координатный параллелизм или, что то же самое, через независимость итераций некоторых циклов (да-да-да, циклы - это понятие, возникающее лишь на этапе реализации, но здесь все так связано… В данном случае, координатный параллелизм означает, что информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей). С этой точки зрения, не менее важен и ресурс скошенного параллелизма. В отличие от координатного параллелизма, скошенный параллелизм намного сложнее использовать на практике, но знать о нем необходимо, поскольку иногда других вариантов и не остается: нужно оценить потенциал алгоритма, и лишь после этого, взвесив все альтернативы, принимать решение о конкретной параллельной реализации. Хорошей иллюстрацией может служить алгоритм, структура которого показана на рис.2: координатного параллелизма нет, но есть параллелизм скошенный, использование которого снижает сложность алгоритма с [math]n\times m[/math] в последовательном случае до [math](n+m-1)[/math] в параллельном варианте.

Рассмотрим алгоритмы, последовательная сложность которых уже оценивалась в п.1.6. Параллельная сложность алгоритма суммирования элементов вектора сдваиванием равна [math]\log_2n[/math], причем число операций на каждом ярусе убывает с [math]n/2[/math] до [math]1[/math]. Параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки - [math]\log_2n[/math]. Параллельная сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это [math]n[/math] шагов для вычислений квадратного корня, [math](n-1)[/math] шагов для операций деления и [math](n-1)[/math] шагов для операций умножения и сложения. <<<

1.9 Входные и выходные данные алгоритма

Вход алгоритма: множество точек X из n-мерного пространства, на котором определена функция расстояния D. В наиболее распространенном случае пространственной кластеризации используется Евлидово расстояние между векторами из [math]\mathbb{R}^n[/math].

Выход алгоритма: размеченное множество точек [math]X[/math], в котором каждой точке соответствует номер ее кластера. Обычно каждой точке из [math]X[/math] сопоставляется ее номер, а на выходе алгоритм дает отображение номеров точек в номера соответствующих им кластеров, например в виде вектора размера [math]|X|[/math].

>>> В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие. <<<

1.10 Свойства алгоритма

1.10.1 Преимущества алгоритма

не требует указывать число кластеров;
может определять кластера произвольной формы;
может определять шум и устойчив к выбросам;
требует всего два параметра и по в большинстве случаев не чувствителен к порядку заданных точек.

1.10.2 Недостатки алгоритма

не детерминирован: граничные точки, достижимые из более, чем одного кластера могут быть частью любого из них, в зависимости от порядка обрабатываемых данных. Однако относительно ядровых точек и шума DBSCAN детерминирован;
качество алгоритма зависит от используемой функции расстояния [math]D[/math]. Наиболее часто используемое Евклидово расстояние в многомерных множествах может оказаться практически бесполезным из-за так называемого "проклятия размерности", значительно затрудняя нахождение подходящего значения [math]\varepsilon[/math];
не может выделять кластеры, имеющие разную плотность, так как параметры алгоритма не могут быть выбранны отдельно для каждого кластера.

>>> Описываются прочие свойства алгоритма, на которые имеет смысл обратить внимание на этапе реализации. Как и ранее, никакой привязки к конкретной программно-аппаратной платформе не предполагается, однако вопросы реализации в проекте AlgoWiki всегда превалируют, и необходимость обсуждения каких-либо свойств алгоритмов определяется именно этим.

Весьма полезным является соотношение последовательной и параллельной сложности алгоритма. Оба понятия мы рассматривали ранее, но здесь делается акцент на том выигрыше, который теоретически может дать параллельная реализация алгоритма. Не менее важно описать и те сложности, которые могут возникнуть в процессе получения параллельной версии алгоритма.

Вычислительная мощность алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных. Несмотря на простоту данного понятия, это значение исключительно полезно на практике: чем выше вычислительная мощность, тем меньше накладных расходов вызывает перемещение данных для их обработки, например, на сопроцессоре, ускорителе или другом узле кластера. Например, вычислительная мощность скалярного произведения двух векторов равна всего лишь [math]1[/math], а вычислительная мощность алгоритма умножения двух квадратных матриц равна [math]2n/3[/math].

Вопрос первостепенной важности на последующем этапе реализации - это устойчивость алгоритма. Все, что касается различных сторон этого понятия, в частности, оценки устойчивости, должно быть описано в данном разделе.

Сбалансированность вычислительного процесса можно рассматривать с разных сторон. Здесь и сбалансированность типов операций, в частности, арифметических операций между собой (сложение, умножение, деление) или же арифметических операций по отношению к операциям обращения к памяти (чтение/запись). Здесь и сбалансированность операций между параллельными ветвями алгоритма. С одной стороны, балансировка нагрузки является необходимым условием эффективной реализации алгоритма. Вместе с этим, это очень непростая задача, и в описании должно быть отмечено явно, насколько алгоритм обладает этой особенностью. Если обеспечение сбалансированности не очевидно, желательно описать возможные пути решения этой задачи.

На практике важна детерминированность алгоритмов, под которой будем понимать постоянство структуры вычислительного процесса. С этой точки зрения, классическое умножение плотных матриц является детерминированным алгоритмом, поскольку его структура при фиксированном размере матриц никак не зависит от элементов входных матриц. Умножение разреженных матриц, когда матрица хранятся в одном из специальных форматов, свойством детерминированности уже не обладает: его свойства, например, степень локальности данных зависит от структуры разреженности входных матриц. Итерационный алгоритм с выходом по точности также не является детерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных. В этом же ряду стоит использование датчиков случайных чисел, меняющих вычислительный процесс для различных запусков программы. Причина выделения свойства детерминированности понятна: работать с детерминированным алгоритмом проще, поскольку один раз найденная структура и будет определять качество его реализации. Если детерминированность нарушается, то это должно быть здесь описано вместе с описанием того, как недетерминированность влияет на структуру вычислительного процесса.

Серьезной причиной недетерминированности работы параллельных программ является изменение порядка выполнения ассоциативных операций. Типичный пример - это использование глобальных MPI-операций на множестве параллельных процессов, например, суммирование элементов распределенного массива. Система времени исполнения MPI сама выбирает порядок выполнения операций, предполагая выполнение свойства ассоциативности, из-за чего ошибки округления меняются от запуска программы к запуску, внося изменения в конечный результат ее работы. Это очень серьезная проблема, которая сегодня встречается часто на системах с массовым параллелизмом и определяет отсутствие повторяемости результатов работы параллельных программ. Данная особенность характерна для второй части AlgoWiki, посвященной реализации алгоритмов, но вопрос очень важный, и соответствующие соображения, по возможности, должны быть отмечены и здесь.

Заметим, что, в некоторых случаях, недетерминированность в структуре алгоритмов можно "убрать" введением соответствующих макроопераций, после чего структура становится не только детерминированной, но и более понятной для восприятия. Подобное действие также следует отразить в данном разделе.

Степень исхода вершины информационного графа показывает, в скольких операциях ее результат будет использоваться в качестве аргумента. Если степень исхода вершины велика, то на этапе реализации алгоритма нужно позаботиться об эффективном доступе к результату ее работы. В этом смысле, особый интерес представляют рассылки данных, когда результат выполнения одной операции используется во многих других вершинах графа, причем число таких вершин растет с увеличением значения внешних переменных.

"Длинные" дуги в информационном графе [1] говорят о потенциальных сложностях с размещением данных в иерархии памяти компьютера на этапе выполнения программы. С одной стороны, длина дуги зависит от выбора конкретной системы координат, в которой расположены вершины графа, а потому в другой системе координат они попросту могут исчезнуть (но не появится ли одновременно других длинных дуг?). А с другой стороны, вне зависимости от системы координат их присутствие может быть сигналом о необходимости длительного хранения данных на определенном уровне иерархии, что накладывает дополнительные ограничения на эффективность реализации алгоритма. Одной из причин возникновения длинных дуг являются рассылки скалярных величин по всем итерациям какого-либо цикла: в таком виде длинные дуги не вызывают каких-либо серьезных проблем на практике.

Для проектирования специализированных процессоров или реализации алгоритма на ПЛИС представляют интерес компактные укладки информационного графа [1], которые также имеет смысл привести в данном разделе.<<<

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Задача данного раздела - показать пределы масштабируемости алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование сильной и слабой масштабируемости алгоритма и его реализаций.

Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).

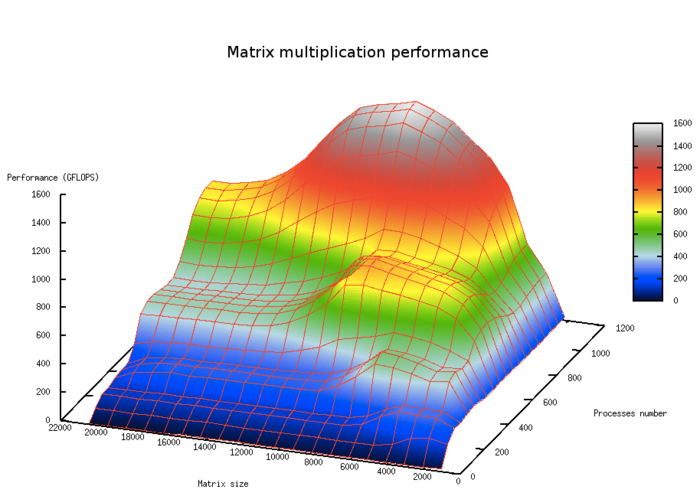
Ключевой момент данного раздела заключается в том, чтобы показать реальные параметры масштабируемости программы для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.

На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.

Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Scikit learn (Python)
R-project (github)
Matlab
P-DBSCAN (Parallel DBSCAN)^[5]
Parallel DBSCAN with MPI^[6]
PDSDBSCAN (Parallel Disjoint-Set DBSCAN)^[7]

>>> Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки. <<<

3 Литература

[1] Пестунов, Игорь Алексеевич, and Юрий Николаевич Синявский. "Алгоритмы кластеризации в задачах сегментации спутниковых изображений." Вестник Кемеровского государственного университета 4.2 (2012).

↑ Ester, Martin, et al. "A density-based algorithm for discovering clusters in large spatial databases with noise." Kdd. Vol. 96. No. 34. 1996.
↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.
↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.
↑ Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.
↑ Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.
↑ Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.
↑ Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.

[1] Ester, Martin, et al. "A density-based algorithm for discovering clusters in large spatial databases with noise." Kdd. Vol. 96. No. 34. 1996.

[2] Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.

[3] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002. – 608 с.

[4] Фролов А.В.. Принципы построения и описание языка Сигма. Препринт ОВМ АН N 236. М.: ОВМ АН СССР, 1989.

[5] Chen, Min, Xuedong Gao, and HuiFei Li. "Parallel DBSCAN with priority r-tree." Information Management and Engineering (ICIME), 2010 The 2nd IEEE International Conference on. IEEE, 2010.

[6] Savvas, Ilias K., and Dimitrios Tselios. "Parallelizing DBSCaN Algorithm Using MPI." Enabling Technologies: Infrastructure for Collaborative Enterprises (WETICE), 2016 IEEE 25th International Conference on. IEEE, 2016.

[7] Patwary, Md Mostofa Ali, et al. "A new scalable parallel DBSCAN algorithm using the disjoint-set data structure." High Performance Computing, Networking, Storage and Analysis (SC), 2012 International Conference for. IEEE, 2012.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Участник:Dadrik/Плотностный алгоритм кластеризации