Участник:Gkhazeeva/Нечеткий алгоритм C средних

Нечеткий алгоритм C средних
Последовательный алгоритм
Последовательная сложность	[math]O(Mdc^2i)[/math], [math]i[/math] - количество итераций
Объём входных данных	[math]M*d[/math], [количество наблюдений * размерность]
Объём выходных данных	[math]M*c[/math], [количество наблюдений * количество кластеров]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]2i[/math]
Ширина ярусно-параллельной формы	[math]n[/math]

Авторы : Гелана Хазеева, Павел Юшин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация - это объединение объектов в группы (кластеры) на основе схожести признаков для объектов одной группы и отличий между группами. Нечеткий алгоритм C Средних (Fuzzy C-means, FCM) - алгоритм кластеризации, позволяющий объектам принадлежать с различной степенью нескольким кластерам одновременно. Впервые алгоритм был предложен J.C. Dunn в 1973 . Нечеткое разбиение позволяет просто решить проблему объектов, расположенных на границе двух кластеров - им назначают степени принадлежностей равные 0.5.

Входные данные алгоритма: набор векторов, которые следует кластеризовать.

Параметры алгоритма: [math]c[/math] - количество кластеров; [math]m[/math] - экспоненциальный вес; [math]\varepsilon[/math] - параметр останова алгоритма.

Выходные данные: матрица вероятностей принадлежности векторов кластерам.

Краткое описание алгоритма:

• Задать параметры алгоритма.

• Сгенерировать случайную матрицу принадлежностей векторов кластерам (матрицу нечеткого разбиения).

• Повторить следующие шаги до момента, пока матрицы нечеткого разбиения на этом и предыдущем шаге алгоритма будут отличать менее чем на параметр останова.
  • Рассчитать центры кластеров.
  • Рассчитать расстоение между объектами и центрами кластеров.
  • Пересчитать элементы матрицы нечеткого разбиения.

1.2 Математическое описание алгоритма

Пусть [math] W = w_{ij} \in[0,1],\; i = 1, ..., M, \; j = 1, ..., c[/math] - матрица разбиения, где [math]w_{i,j}[/math] - степень принадлежности объекта [math]i[/math] к кластеру [math]j[/math]; [math]c[/math] - количество кластеров, [math]M[/math] - количество векторов.

При этом элементы матрицы должны удовлетворять условиям:

• [math]\sum_{j = 1}^c w_{ij} = 1, i = 1, ..., M[/math] [math](1)[/math]
• [math]0 \lt \sum_{i = 1}^M w_{ij} \lt M, j = 1, ..., c[/math] [math](2)[/math]

Тогда алгоритм принимает следующий вид:

1) Задаем параметры алгоритма: [math]c[/math] - количество кластеров; [math]m \gt = 1[/math] - экспоненциальный вес, определяющий нечеткость кластеров; [math]\varepsilon \gt 0[/math] - параметр останова алгоритма.

2) Генерируем случайным образом матрицу нечеткого разбиения с учетом условий [math](1)[/math] и [math](2)[/math]

3) Рассчитываем центроиды (центры кластеров): [math]V_j = {{\sum_{i=1}^M w_{ij}^m * X_i} \over {\sum_{i=1}^M w_{ij}^m}}, j = 1, ..., c[/math]

4) Рассчитываем расстояния между объектами [math]X[/math] и центроидами:

[math]D_{ij} = {||X_i - V_j||}, i = 1,...,M; j = 1,...,c [/math]

5) Пересчет элементов матрицы разбиения:

при [math]D_{ij} \gt 0[/math] : [math]w_{ij} = {{1}\over {{ (\sum_{k=1}^c {{D_{ij}}\over{D_{ik}}} ) }^{2/(m-1)}}}, j = 1,...,c[/math]

при [math]D_{ij} =0[/math] : [math]w_{ij} = \delta_{ij}, j = 1,...,c[/math], где [math]\delta_{ij}[/math] - символ Кронекера

6) Если [math]|| F - F^{*} || \lt \varepsilon [/math], где [math]F^{*}[/math] - матрица нечеткого разбиения предыдущей итерации, то идем далее, иначе возвращаемся на пункт 3.

7) Конец.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма являются пункты (3), (4), (5) - расчет центроидов, вычисление расстояний и пересчет элементов матрицы соответственно

1.4 Макроструктура алгоритма

Основные шаги при реализации алгоритма

• Генерация случайной матрицы размера [math]M[/math] на где [math]c[/math], проверка условий
• Расчет центроидов – по сути, скалярное произведение с нормировкой
• Расчет расстояний – в общепринятом случае является скалярным произведением
• Пересчет матрицы – по сути, скалярное произведение
• Проверка условий останова – вычисление нормы

1.5 Схема реализации последовательного алгоритма

   float ** FuzzyCMeans (float** X, c, m, eps){
       n = X.size();
       r = X[0].size();
       centers = generateZeroFill(c, r)
       Wprev = genetateRandFill(n, c);
       W = Wprev;
       while (true){
           // обновляем центры кластеров 
           for (int i=0; i<c; i++){
               float * num = new float []();
               float den = 0;
               for (int j=0; j<n; j++){
                   num += pow(W[j][i], m) * X[j];
                   den+=pow(W[j][i], m);
               }
               centers[i] = num / den;
           }
           //обновляем вероятности W и считаем расстояние между матрицами W и Wprev
           float max_diff = 0;
           for (int i=0; i<n; i++)
               for (int j=0; j<c; j++){
                   total = 0;
                   for (int m=0; m<с; m++)
                       total += pow(distance(X[i], centers[j]) / distance(X[i], centers[m]), 2/(m-1));
                   W[i][j] = 1/total;
                   max_diff = max(abs(Wprev[i][j]-W[i][j]), max_diff);
                   Wprev[i][j] = W[i][j];
              }               
          if (max_diff < eps):                
               break;
       }
       return W;
   }

1.6 Последовательная сложность алгоритма

Последовательная сложность алгоритма состоит из сложности каждой итерации умноженной на их количество. Так как число итераций заранее неизвестно и зависит от входных параметров, рассмотрим сложность на каждой итерации. Наибольшую сложность представляет собой пересчет матрицы, сложность которого [math]O(c^2 nd)[/math] (по сравнению со сложностью [math]O(cnd)[/math] расчета расстояний, вычисления центроидов и проверки условия останова). Итого общая сложность алгоритма [math]O(c^2 ndi)[/math]

1.7 Информационный граф

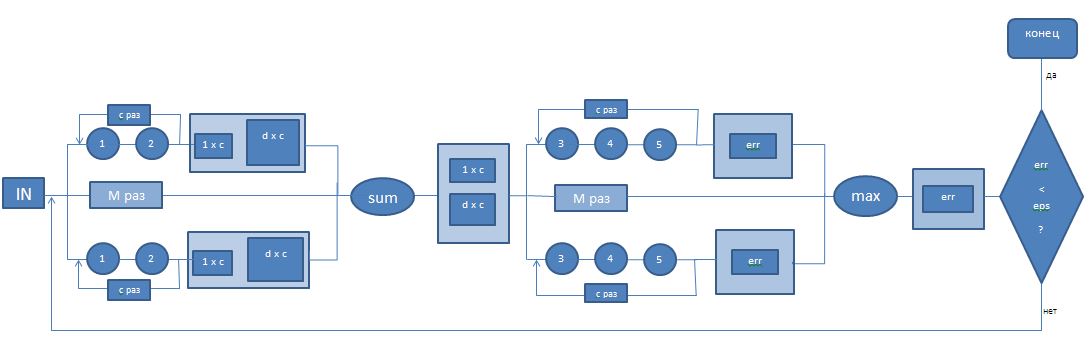
Информационный граф представлен на рисунке ниже.

Первый ярус состоит из [math]M[/math] параллельных операций 1, 2, совершаемых в цикле [math]c[/math] раз для каждого кластера.

Операция 1: [math]w_{ij}^m[/math], где [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

Операция 2: [math]w_{ij}^m*X_i[/math]

Здесь [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

На выходе из каждой ветки получаем вектор размера [math]1[/math] x [math]c[/math] и матрицу размера [math]d[/math] x [math]c[/math]. Далее совершаем поэлементное сложение векторов и матриц соответственно, а затем делим каждый столбец в матрице на соответствующий элемент в векторе.

Второй ярус состоит их [math]M[/math] параллельных операций 3, 4, 5 также совершаемых в цикле [math]c[/math] раз.

Операция 4: обновление значения [math]w_{ij}[/math] по указанной в разделе 1.2 в пункте 5 формуле.

Операция 5: [math]maximum = max(|w_{ij} - w_{ij}^{prev}|, maximum)[/math].

Операция 6: [math]w_{ij}^{prev} = w_{ij}[/math].

Здесь [math]j[/math] - номер итерации в цикле, [math]i[/math] - номер параллельной ветви.

На выходе из каждой ветки получаем число [math]maximum[/math]. Далее находим максимальное значение из полученных величин для каждой ветки. Затем проверяем условие останова алгоритма.

1.8 Ресурс параллелизма алгоритма

Параллельная сложность алгоритма: [math]M*c^2*i[/math]. Такая сложность получается за счет распараллеливания на каждом ярусе [math]M[/math] операций. Иерархическая структура параллелизма подробно описана в п.1.7.

В алгоритме не возникает скошенного параллелизма.

1.9 Входные и выходные данные алгоритма

• Входные данные алгоритма: набор векторов [math]x_i[/math] размерности [math]d[/math], где [math]i = 1,...,M[/math]; [math]M[/math] - количество векторов.
• Выходные данные алгоритма: матрица вероятностей принадлежности векторов кластерам [math]M[/math] на [math]c[/math].

1.10 Свойства алгоритма

• Соотношение последовательной и параллельной формы алгоритма: [math]M[/math]
• Вычислительная мощность: [math]{dc^2i} \over {c+d}[/math].
• Устойчивость: алгоритм не является устойчивым, поэтому существует много исследований о том, как первоначально выбрать параметры кластеризации.
• Сбалансированность: в данном алгоритме операция умножения доминирует над операцией сложения. Операции между параллельными ветвями сбалансированны.
• Детерминированность: алгоритм не является детерминированным, так как матрица нечеткого разбиение генерируется произвольно.
• Степень исхода вершины информационного графа ( для одной интерации): 2 (3 - с учетом, если выходные данные пошли на следующую итерацию).

2 Программная реализация алгоритма

2.2 Существующие реализации алгоритма

• Реализация алгоритма на POSTGRESQL: http://num-meth.srcc.msu.ru/zhurnal/tom_2012/pdf/v13r207.pdf
• Библиотека для MATLAB: http://www.mathworks.com/help/fuzzy/fcm.html (распространяется на коммерческой основе)