Участник:NataliaPolienko/Блочное умножение матриц по методу Кеннона
Автор: Полиенко Н.А.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Одной из основных операций над матрицами является их перемножение. Данная операция широко применяется в большом количестве разных методов. Здесь мы рассмотрим умножение [math]C = AB[/math] квадратных матриц с помощью алгоритма Кеннона. Его суть заключается в том, что матрицы разбиваются на блоки, представляющие собой подматрицы исходных матриц. В следствии чего в качестве базовой подзадачи можно выбрать вычисления, связанные с определением одного из блоков результирующей матрицы [math]C[/math] [1].
1.2 Математическое описание алгоритма
Исходные данные: матрица [math]A[/math] размера [math]n \times n[/math], матрица [math]B[/math] размера [math]n \times n[/math].
Вычисляемые данные: матрица [math]C[/math] размера [math]n \times n[/math].
Исходные и результирующая матрицы представляются в виде наборов блоков. Операцию матричного умножения матриц [math]A[/math] и [math]B[/math] в блочном виде можно представить следующим образом [2]: [math] \begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1k} \\ A_{21} & A_{22} & \cdots & A_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ A_{k1} & A_{k2} & \cdots & A_{kk} \end{bmatrix} \begin{bmatrix} B_{11} & B_{12} & \cdots & B_{1k} \\ B_{21} & B_{22} & \cdots & B_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ B_{k1} & B_{k2} & \cdots & B_{kk} \end{bmatrix} = \begin{bmatrix} C_{11} & C_{12} & \cdots & C_{1k} \\ C_{21} & C_{22} & \cdots & C_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ C_{k1} & C_{k2} & \cdots & C_{kk} \end{bmatrix}, [/math]
где каждый блок [math]C_{ij}[/math] матрицы [math]C[/math] определяется в соответствии с выражением:
- [math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
Полученные блоки [math]C_{ij}[/math] являются независимыми.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро перемножения матриц(квадратных) методом Кеннона можно составить из множественных вычислений умножения блоков матрицы [math]A[/math] на блоки матрицы [math]B[/math], таким образом получая блок результирующей матрицы [math]C[/math]:
- [math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
1.4 Макроструктура алгоритма
Как записано в описании ядра алгоритма, основную часть метода составляют множественные вычисления умножений блоков матрицы [math]A[/math] на блоки матрицы [math]B[/math]:
- [math] \begin{align} \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
1.5 Схема реализации последовательного алгоритма
Алгоритм осуществляет последовательное вычисление блоков результирующей матрицы [math]C[/math]: 1. Матрицы [math]A[/math], [math]B[/math] разбиваются на блоки фиксированного размера(будем предполагать, что блоки квадратные и порядок матрицы делится на размер блока без остатка). 2. На одной итерации цикла по переменной [math]i[/math] используется первая строка, состоящая из блоков матрицы [math]A[/math] и все столбцы, состоящие из блоков матрицы [math]B[/math]: [math] \begin{align} C_{ij} = \sum_{l = 1}^{k} A_{il} B_{lj}, \quad i \in [1, k], \quad j \in [1, k]. \end{align} [/math]
1.6 Последовательная сложность алгоритма
Для перемножения матриц размера [math]n \times n[/math] в последовательной реализации алгоритма требуется [math]n^3[/math] умножений и сложений.
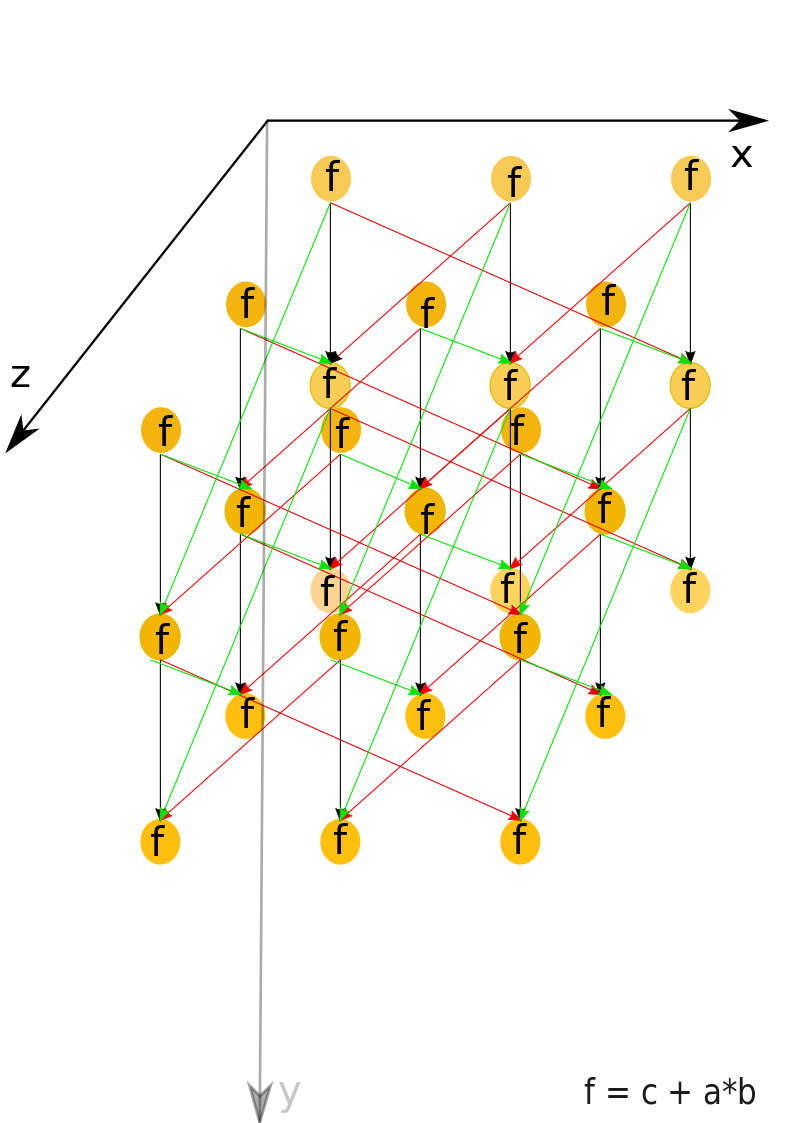
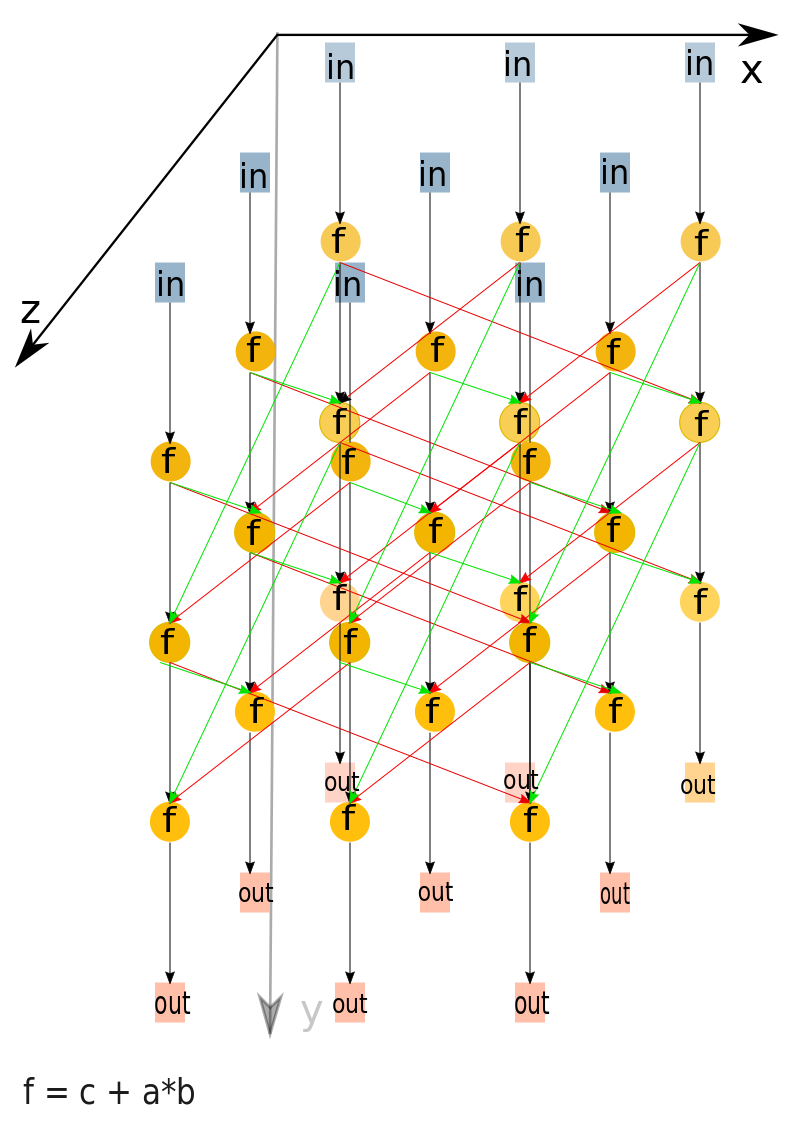
1.7 Информационный граф
Опишем граф алгоритма[3] как аналитически, так и в виде рисунка.
Граф алгоритма умножения квадратных матриц методом Кеннона состоит из одной группы вершин, расположенной в целочисленных узлах трёхмерной области, соответствующая ей операция вычисляет функцию f, где [math]f = с+a*b[/math].
Естественно введённые координаты области таковы:
- [math]i[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения;
- [math]j[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения;
- [math]k[/math] — меняется в диапазоне от [math]1[/math] до [math]m[/math], принимая все целочисленные значения.
Аргументы операции следующие:
- [math]k = 1[/math]:
- [math]c = 0[/math];
- [math]a[/math]: элемент входных данных, а именно блок матрицы [math]A[/math] с координатами [math]i, j[/math];
- [math]b[/math] - элемент входных данных, а именно блок матрицы [math]B[/math] с координатами [math]i, j[/math];
- [math]k \gt 1[/math]:
- [math]c[/math] - результат срабатывания операции, соответствующей вершине с координатами [math]i, j, k-1[/math];
- [math]a[/math]: элемент, переданный из вершины [math]i, j+1, k-1[/math], являющийся элементом(блоком) матрицы [math]A[/math];
- [math]b[/math]: элемент, переданный из вершины [math]i+1, j, k-1[/math], являющийся элементом(блоком) матрицы [math]B[/math];
При [math]k \lt m[/math] - результатом выполнения операции является промежуточные данные алгоритма; При [math]k = m[/math] - выходными данными алгоритма([math]C_{ij}[/math]) будут являться результаты выполнения операции в узлах.
Описанный граф можно посмотреть на рис.1 и рис.2, выполненных для случая [math]m = 3[/math]([math]m [/math] - количество блоков, на которые разбиты исходные матрицы [math]A[/math] и [math]B[/math] ).Здесь красными стрелками указана циклическая передача данных, соответствующих блоку матрицы [math]A[/math], а зелеными стрелка - матрицы [math]B[/math]. На рис.1 показан граф алгоритма согласно классическому определению , на рис.2 к графу алгоритма добавлены вершины , соответствующие входным (обозначены синим цветом) и выходным (обозначены розовым цветом) данным.
1.8 Ресурс параллелизма алгоритма
Для алгоритма умножения квадратных матриц методом Кеннона размера [math]n \times n[/math] в параллельном варианте требуется последовательно выполнить следующие ярусы:
- по [math]m/k[/math] ярусов умножений и сложений (в каждом из ярусов — [math](m/k)^2[/math] операций, где [math]m/k[/math] - количество элементов в блоке).
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.
При классификации по высоте ЯПФ, таким образом, алгоритм умножения матриц относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет квадратичной (для квадратных матриц) или билинейной (для матриц общего вида).
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math], матрица [math]B[/math].
Объём входных данных: [math]n \times n + n \times n[/math]
Выходные данные: матрица [math]C[/math] .
Объём выходных данных: [math]n \times n[/math]
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ http://www.math.tsu.ru/sites/default/files/mmf2/e-resources/Introduction_to_Parallel_Computations_L4(6).pdf
- ↑ http://www.intuit.ru/studies/courses/1156/190/lecture/4964?page=7
- ↑ Воеводин В.В. Математические основы параллельных вычислений// М.: Изд. Моск. ун-та, 1991. 345 с.