Уровень алгоритма

Участник:Shostix/Алгоритм Ланцоша для точной арифметики (без переортогонализации): различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
Строка 1: Строка 1:
 
{{algorithm
 
{{algorithm
−
| name = Алгоритм Ланцоша для точной арифметики (без ортогонализации)
+
| name             = Алгоритм Ланцоша для точной арифметики (без ортогонализации)
 
| serial_complexity = <math>O(kn^2)</math>
 
| serial_complexity = <math>O(kn^2)</math>
−
| input_data        = <math>n*(n-1)+2</math>
+
| input_data        = <math>\frac{n(n+1)}{2} + 1</math>
−
| output_data = <math>k*(n+1)</math>
+
| output_data       = <math>kn+k</math>
−
| pf_height = <math>O(k*log(n))</math>
+
| pf_height         = <math>O(k*log(n))</math>
−
| pf_width = <math>O(n^2)</math>
+
| pf_width         = <math>O(n^2)</math>
 
}}
 
}}
  
Строка 15: Строка 15:
 
=== Общее описание алгоритма ===
 
=== Общее описание алгоритма ===
  
−
'''Алгоритм Ланцоша''' - один из итерационных методов вычисления собственных значений симметричных матриц. Используется для работы с матрицами столь большими, что классические численные методы нахождения собственных значений наприменимы из-за высокой вычислительной сложности.
+
'''Алгоритм Ланцоша''' - один из итерационных методов вычисления собственных значений и собственных векторов симметричных матриц (задача <math>Ax = \lambda x</math>). Используется для работы с матрицами столь большими, что классические численные методы нахождения собственных значений неприменимы из-за высокой вычислительной сложности. На практике чаще всего используется для работы с большими разреженными матрицами.
  
−
Алгоритм был предложен в 1950 году венгерским физиком и математиком Корнелием Ланцошем. Основан на методе Ланцоша для построения крыловского подпространства и процедуре Рэлея-Ритца.
+
Алгоритм был предложен в 1950 году венгерским физиком и математиком Корнелием Ланцошем. Основан на понятии построения крыловского подпространства и процедуре Рэлея-Ритца: строит последовательность трехдиагональных матриц с тем свойством, что экстремальные собственные значения для каждой последующей трехдиагональной матрицы дают все более точные оценки экстремальных собственных значений для А.  
  
−
В данной статье будет рассмотрен простой метод Ланцоша (без ортогонализации). Он не является устойчивым к влиянию ошибок округления, в отличие от своих модификаций - алгоритма Ланцоша с выборочной ортогонализацией и полной ортогонализацией. На практике часто применяется алгоритм Ланцоша с полной ортогонализацией, предложенный в 1970 году. Он является оптимальным по точности вычислений, хоть и наиболее дорогостоящим алгоритмом из указанных.
+
В данной статье будет рассмотрен простой метод Ланцоша (без ортогонализации). К сожалению, на практике использование метода Ланцоша без ортогонализации затруднено ошибками округления. Центральная проблема - это потеря ортогональности получаемых итерационно векторов Ланцоша. Такая проблема решается усовершенствованием алгоритма Ланшоца (алгоритмами Ланшоца с выборочной и полной ортогонализацией)<ref>Деммель Д. Вычислительная линейная алгебра</ref>.
  
−
Для наименее дорогостоящего в вычислениях алгоритма Ланцоша без ортогонализации будем подразумевать отсутствие влияния ошибок округления на вычислительный процесс.  
+
В данной статье будем подразумевать отсутствие влияния ошибок округления на вычислительный процесс.  
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
 +
 +
''Исходные данные'':
 +
 +
*  симметрическая матрица <math>A=A^T</math> размерности <math>n</math>, элементы матрицы <math>a_{ij}=a_{ji}</math>
 +
*  начальный вектор <math>v = {v_1, v_2, ..., v_n}, v \neq \theta</math>
 +
Так как матрица является симметрической, достаточно хранить <math>\frac{n(n+1)}{2}</math> ее элементов.
 +
 +
Для исходной матрицы <math>A</math> и вектора <math>v</math> строится крыловское подпространство. Крыловское подпространство - это линейная оболочка векторов <math>[v, Av, A^2v, ..., A^{k-1}v]</math>, называемых векторами Ланцоша.
 +
Каждый из векторов Ланцоша ортонормируется: <math>q_k=\frac{A^kv}{\|A^kv\|}</math>, и на шаге <math>k</math> алгоритма имеется Крыловская матрица <math>Q = {q_0, ..., q_{k-1}}</math> размерности <math>n \times k</math>.
 +
 +
Соответствующий текущей итерации <math>k</math> вектор Ланцоша считается <math>k</math>-ым приближением собственного вектора исходной матрицы <math>A</math>.
 +
В качестве приближенных собственных значений матрицы <math>A</math> берутся собственные значения симметричной трехдиагональной матрицы <math>T_k = Q^T_k A Q</math> (числа Ритца). В качестве алгоритма нахождения собственных векторов и собственных значений симметрической трехдиагональной матрицы будем использовать метод "разделяй и властвуй", который требует <math>O(k^3)</math> операций.<ref>https://en.wikipedia.org/wiki/Divide-and-conquer_eigenvalue_algorithm</ref>.
 +
 +
''Выходные данные'':
 +
 +
* совокупность собственных векторов матрицы <math>T_k</math> (т.е. <math>k</math>-ых приближений собственных векторов матрицы <math>A</math>)
 +
* совокупность собственных значений матрицы <math>T_k</math> (т.е. <math>k</math>-ых приближений собственных значений матрицы <math>A</math>)
 +
 +
=== Вычислительное ядро алгоритма ===
 +
 +
'''Вычислительное ядро'''. т.е. часть алгоритма, требующая наибольших вычислительных затрат на каждой итерации состоит из вычисления промежуточного вектора <math>z=Aq_i</math>
 +
 +
=== Макроструктура алгоритма ===
 +
''' Итерация алгоритма: '''
 +
* вычисление нормы вектора,
 +
* деление вектора на число,
 +
* умножение матрицы на вектор,
 +
* линейная комбинация векторов (умножение на число и сложение).
 +
 +
''' Финальный расчет: '''
 +
* вычисление собственных векторов и собственных значений трехдиагональной симметричной матрицы.
 +
 +
=== Схема реализации последовательного алгоритма ===
 +
 +
''Псевдокод алгоритма''<ref>Деммель Д. Вычислительная линейная алгебра</ref>:
 +
 +
'''Вход'''  : размерность матрицы <math>n</math>, элементы симметричной матрицы <math>A</math>, количество итераций <math>k</math>
 +
'''Выход''' : собственные вектора матрицы <math>T_k</math>, матрица собственных значений
 +
<math>
 +
\begin{align}
 +
q_1 = & b/ \|b\|_2,\;
 +
\beta_0 = 0,\;
 +
q_0 = 0\\
 +
for \; & i = 1 \; to \; k \\
 +
& z = Aq_i\\
 +
& \alpha_i = q^T_i z\\
 +
& z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}\\
 +
& \beta_i = \|z\|_2\\
 +
& If \; \beta_i == 0 \; then \\
 +
& \; \; \; \; exit\\
 +
& else \\
 +
& \; \; \; \; q_{i+1} = z / \beta_i \\
 +
end \; & for
 +
\end{align};
 +
</math>
 +
 +
<math>procedure(T_k)</math>;
 +
 +
<math>procedure()</math> - процедура вычисления собственных векторов и собственных значений симметрической трехдиагональной матрицы.
 +
 +
=== Последовательная сложность алгоритма ===
 +
 +
Глобально алгоритм состоит из инициализации, <math>k</math> итераций и финального расчета собственных векторов и собственных значений.
 +
 +
Рассмотрим сложность каждой макрооперации алгоритма:
 +
* вычисление нормы вектора - <math>(n-1)</math> сложений, <math>n</math> умножений, операция извлечения корня
 +
* деление вектора на число - <math>n</math> операций
 +
* умножение матрицы на вектор - <math>n^2</math> операций
 +
* скалярное произведение векторов - <math>n</math> операций
 +
* линейная комбинация векторов - <math>2n</math> умножений и вычитаний
 +
* вычисление собственных векторов и собственных значений матрицы <math>T_k</math> методом "Разделяй и властвуй"  - <math>O(k^3)</math> операций.
 +
 +
'''Инициализация:'''
 +
* вычисление нормы вектора,
 +
* деление вектора на число.
 +
'''Одна итерация:'''
 +
* умножение матрицы на вектор,
 +
* скалярное произведение векторов,
 +
* линейная комбинация векторов,
 +
* вычисление нормы вектора,
 +
* деление вектора на число.
 +
'''Финальный расчет:'''
 +
* вычисление собственных векторов и собственных значений матрицы
 +
 +
Итого '''последовательная сложность алгоритма''' составляет <math>O(3n+k(n^2+n+2n+2n+3n))+O(k^3)</math>.
 +
 +
Так как на практике порядок матрицы <math>n</math> намного превышает количество итераций <math>k</math>, сложность алгоритма Ланцоша можно рассматривать <math>O(kn^2)</math>.
 +
 +
=== Информационный граф ===
 +
 +
Информационный граф алгоритма с входными и выходными данными можно описать в виде рисунка:
 +
 +
[[Файл:Ланцош.png|600px|thumb|center|Рисунок 1. Информационный граф алгоритма Ланцоша.<br/>
 +
<math>\|.\|</math> — операция вычисления нормы, <br/>
 +
<math>/</math> — операция деления, <br/>
 +
<math>A</math> — операция умножения матрицы на вектор, <br/>
 +
<math>*</math>  — операция скалярного произведения,<br/>
 +
<math>L</math> — операция вычисления линейной комбинации векторов, <br/>
 +
▽ - проверка условия <math>\mathsf{(\beta_i = 0)}</math> и выход из цикла в случае выполнения условия]]
 +
 +
=== Ресурс параллелизма алгоритма ===
 +
 +
Внутри каждой итерации алгоритма можно задействовать параллельные вычисления для суммирования векторов (использовать суммирование методом сдваивания элементов). Эта операция будет использована в макрооперации умножения матрицы на вектор, которая требует в последовательной реализации <math>n</math> умножений и <math>n-1</math> сложение. В таком виде сложение <math>n</math> элементов можно выполнить за <math>\log_2 n</math> действий.
 +
 +
=== Входные и выходные данные алгоритма ===
 +
 +
''Входные данные'': симметрическая матрица <math>A=A^T</math> размерности <math>n</math>, количество итераций <math>k</math>.
 +
 +
''Объем входных данных'': <math>\frac{n(n+1)}{2} + 1</math>.
 +
 +
''Выходные данные'': <math>k</math> собственных векторов, собственных значений матрицы на <math>k</math>-ом приближении.
 +
 +
''Объем выходных данных'': <math>kn+k</math>.
 +
 +
=== Свойства алгоритма ===
 +
 +
* Сложность последовательной реализации алгоритма <math>O(kn^2)</math>.
 +
* Сложность параллельного алгоритма Ланцоша по высоте ЯПФ <math>O(k\log n)</math>, по ширине ЯПФ <math>O(n^2)</math>.
 +
** В умножении матрицы на вектор сложение n элементов выполняется в <math>\log_2 n</math> ярусов шириной <math>\frac{n}{2}, \frac{n}{4}, ... , 1</math>, остальные операции внутри итерации выполняются последовательно
 +
* Отношение последовательной сложности  к параллельной <math>\frac{kn^2}{k \log{n}}</math>.
 +
* Вычислительная мощность алгоритма Ланцоша из последовательной сложности алгоритма <math>\frac{k(2n^2+8n-1)+3n}{n^2+2k}</math>. Учитывая <math>k</math> много меньше  <math>n</math>, вычислительная мощность ≈ <math> 2k</math>.
 +
* В алгоритме Ланцоша возможно выполнение числа итераций менее <math>k</math> если все собственные значения матрицы вычисляются раньше.
 +
* Для найденных собственных значений справедливо: <math>\lambda_i(T_{k+1})\geq \lambda_i(T_{k})\geq \lambda_{i+1}(T_{k+1})\geq \lambda_{i+1}(T_{k})</math>, т.е. в первую очередь находятся максимальные по модулю собственные значения.
 +
* Как следствие предыдущего пункта алгоритм Ланцоша особенно удобен для вычисления собственных значений матрицы, находящихся на границе ее спектра.
 +
 +
== Программная реализация алгоритма ==
 +
 +
=== Особенности реализации последовательного алгоритма ===
 +
=== Локальность данных и вычислений ===
 +
 +
=== Возможные способы и особенности параллельной реализации алгоритма ===
 +
 +
=== Масштабируемость алгоритма и его реализации ===
 +
 +
 +
=== Динамические характеристики и эффективность реализации алгоритма ===
 +
=== Выводы для классов архитектур ===
 +
=== Существующие реализации алгоритма ===
 +
 +
== Литература ==

Версия 11:29, 24 января 2017


Алгоритм Ланцоша для точной арифметики (без ортогонализации)
Последовательный алгоритм
Последовательная сложность [math]O(kn^2)[/math]
Объём входных данных [math]\frac{n(n+1)}{2} + 1[/math]
Объём выходных данных [math]kn+k[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]O(k*log(n))[/math]
Ширина ярусно-параллельной формы [math]O(n^2)[/math]


Авторы:

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша - один из итерационных методов вычисления собственных значений и собственных векторов симметричных матриц (задача [math]Ax = \lambda x[/math]). Используется для работы с матрицами столь большими, что классические численные методы нахождения собственных значений неприменимы из-за высокой вычислительной сложности. На практике чаще всего используется для работы с большими разреженными матрицами.

Алгоритм был предложен в 1950 году венгерским физиком и математиком Корнелием Ланцошем. Основан на понятии построения крыловского подпространства и процедуре Рэлея-Ритца: строит последовательность трехдиагональных матриц с тем свойством, что экстремальные собственные значения для каждой последующей трехдиагональной матрицы дают все более точные оценки экстремальных собственных значений для А.

В данной статье будет рассмотрен простой метод Ланцоша (без ортогонализации). К сожалению, на практике использование метода Ланцоша без ортогонализации затруднено ошибками округления. Центральная проблема - это потеря ортогональности получаемых итерационно векторов Ланцоша. Такая проблема решается усовершенствованием алгоритма Ланшоца (алгоритмами Ланшоца с выборочной и полной ортогонализацией)[1].

В данной статье будем подразумевать отсутствие влияния ошибок округления на вычислительный процесс.

1.2 Математическое описание алгоритма

Исходные данные:

  • симметрическая матрица [math]A=A^T[/math] размерности [math]n[/math], элементы матрицы [math]a_{ij}=a_{ji}[/math]
  • начальный вектор [math]v = {v_1, v_2, ..., v_n}, v \neq \theta[/math]

Так как матрица является симметрической, достаточно хранить [math]\frac{n(n+1)}{2}[/math] ее элементов.

Для исходной матрицы [math]A[/math] и вектора [math]v[/math] строится крыловское подпространство. Крыловское подпространство - это линейная оболочка векторов [math][v, Av, A^2v, ..., A^{k-1}v][/math], называемых векторами Ланцоша. Каждый из векторов Ланцоша ортонормируется: [math]q_k=\frac{A^kv}{\|A^kv\|}[/math], и на шаге [math]k[/math] алгоритма имеется Крыловская матрица [math]Q = {q_0, ..., q_{k-1}}[/math] размерности [math]n \times k[/math].

Соответствующий текущей итерации [math]k[/math] вектор Ланцоша считается [math]k[/math]-ым приближением собственного вектора исходной матрицы [math]A[/math]. В качестве приближенных собственных значений матрицы [math]A[/math] берутся собственные значения симметричной трехдиагональной матрицы [math]T_k = Q^T_k A Q[/math] (числа Ритца). В качестве алгоритма нахождения собственных векторов и собственных значений симметрической трехдиагональной матрицы будем использовать метод "разделяй и властвуй", который требует [math]O(k^3)[/math] операций.[2].

Выходные данные:

  • совокупность собственных векторов матрицы [math]T_k[/math] (т.е. [math]k[/math]-ых приближений собственных векторов матрицы [math]A[/math])
  • совокупность собственных значений матрицы [math]T_k[/math] (т.е. [math]k[/math]-ых приближений собственных значений матрицы [math]A[/math])

1.3 Вычислительное ядро алгоритма

Вычислительное ядро. т.е. часть алгоритма, требующая наибольших вычислительных затрат на каждой итерации состоит из вычисления промежуточного вектора [math]z=Aq_i[/math]

1.4 Макроструктура алгоритма

Итерация алгоритма:

  • вычисление нормы вектора,
  • деление вектора на число,
  • умножение матрицы на вектор,
  • линейная комбинация векторов (умножение на число и сложение).

Финальный расчет:

  • вычисление собственных векторов и собственных значений трехдиагональной симметричной матрицы.

1.5 Схема реализации последовательного алгоритма

Псевдокод алгоритма[3]: 

Вход  : размерность матрицы [math]n[/math], элементы симметричной матрицы [math]A[/math], количество итераций [math]k[/math]
Выход : собственные вектора матрицы [math]T_k[/math], матрица собственных значений

[math] \begin{align} q_1 = & b/ \|b\|_2,\; \beta_0 = 0,\; q_0 = 0\\ for \; & i = 1 \; to \; k \\ & z = Aq_i\\ & \alpha_i = q^T_i z\\ & z = z - \alpha_i q_i - \beta_{i-1}q_{i-1}\\ & \beta_i = \|z\|_2\\ & If \; \beta_i == 0 \; then \\ & \; \; \; \; exit\\ & else \\ & \; \; \; \; q_{i+1} = z / \beta_i \\ end \; & for \end{align}; [/math]

[math]procedure(T_k)[/math];

[math]procedure()[/math] - процедура вычисления собственных векторов и собственных значений симметрической трехдиагональной матрицы.

1.6 Последовательная сложность алгоритма

Глобально алгоритм состоит из инициализации, [math]k[/math] итераций и финального расчета собственных векторов и собственных значений.

Рассмотрим сложность каждой макрооперации алгоритма:

  • вычисление нормы вектора - [math](n-1)[/math] сложений, [math]n[/math] умножений, операция извлечения корня
  • деление вектора на число - [math]n[/math] операций
  • умножение матрицы на вектор - [math]n^2[/math] операций
  • скалярное произведение векторов - [math]n[/math] операций
  • линейная комбинация векторов - [math]2n[/math] умножений и вычитаний
  • вычисление собственных векторов и собственных значений матрицы [math]T_k[/math] методом "Разделяй и властвуй" - [math]O(k^3)[/math] операций.

Инициализация:

  • вычисление нормы вектора,
  • деление вектора на число.

Одна итерация:

  • умножение матрицы на вектор,
  • скалярное произведение векторов,
  • линейная комбинация векторов,
  • вычисление нормы вектора,
  • деление вектора на число.

Финальный расчет:

  • вычисление собственных векторов и собственных значений матрицы

Итого последовательная сложность алгоритма составляет [math]O(3n+k(n^2+n+2n+2n+3n))+O(k^3)[/math].

Так как на практике порядок матрицы [math]n[/math] намного превышает количество итераций [math]k[/math], сложность алгоритма Ланцоша можно рассматривать [math]O(kn^2)[/math].

1.7 Информационный граф

Информационный граф алгоритма с входными и выходными данными можно описать в виде рисунка:

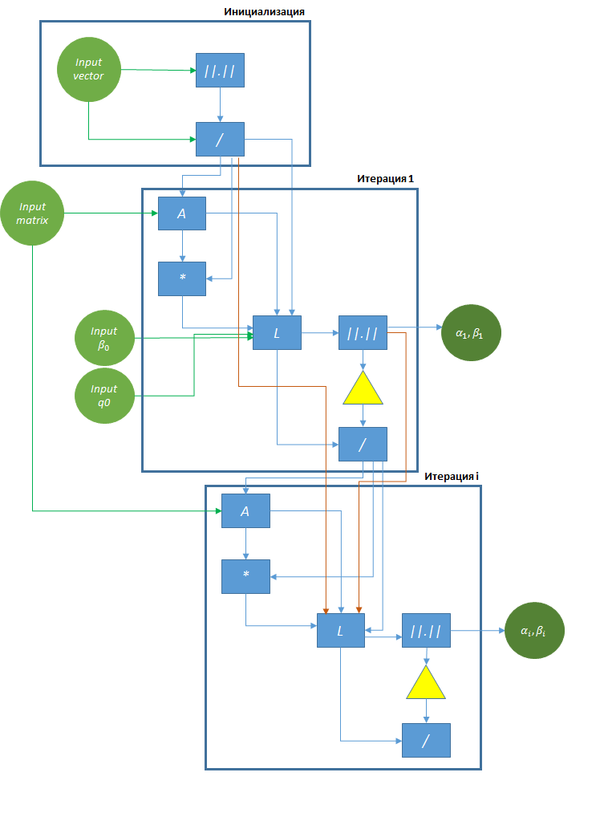
Рисунок 1. Информационный граф алгоритма Ланцоша.
[math]\|.\|[/math] — операция вычисления нормы,
[math]/[/math] — операция деления,
[math]A[/math] — операция умножения матрицы на вектор,
[math]*[/math] — операция скалярного произведения,
[math]L[/math] — операция вычисления линейной комбинации векторов,
▽ - проверка условия [math]\mathsf{(\beta_i = 0)}[/math] и выход из цикла в случае выполнения условия

1.8 Ресурс параллелизма алгоритма

Внутри каждой итерации алгоритма можно задействовать параллельные вычисления для суммирования векторов (использовать суммирование методом сдваивания элементов). Эта операция будет использована в макрооперации умножения матрицы на вектор, которая требует в последовательной реализации [math]n[/math] умножений и [math]n-1[/math] сложение. В таком виде сложение [math]n[/math] элементов можно выполнить за [math]\log_2 n[/math] действий.

1.9 Входные и выходные данные алгоритма

Входные данные: симметрическая матрица [math]A=A^T[/math] размерности [math]n[/math], количество итераций [math]k[/math].

Объем входных данных: [math]\frac{n(n+1)}{2} + 1[/math].

Выходные данные: [math]k[/math] собственных векторов, собственных значений матрицы на [math]k[/math]-ом приближении.

Объем выходных данных: [math]kn+k[/math].

1.10 Свойства алгоритма

  • Сложность последовательной реализации алгоритма [math]O(kn^2)[/math].
  • Сложность параллельного алгоритма Ланцоша по высоте ЯПФ [math]O(k\log n)[/math], по ширине ЯПФ [math]O(n^2)[/math].
    • В умножении матрицы на вектор сложение n элементов выполняется в [math]\log_2 n[/math] ярусов шириной [math]\frac{n}{2}, \frac{n}{4}, ... , 1[/math], остальные операции внутри итерации выполняются последовательно
  • Отношение последовательной сложности к параллельной [math]\frac{kn^2}{k \log{n}}[/math].
  • Вычислительная мощность алгоритма Ланцоша из последовательной сложности алгоритма [math]\frac{k(2n^2+8n-1)+3n}{n^2+2k}[/math]. Учитывая [math]k[/math] много меньше [math]n[/math], вычислительная мощность ≈ [math] 2k[/math].
  • В алгоритме Ланцоша возможно выполнение числа итераций менее [math]k[/math] если все собственные значения матрицы вычисляются раньше.
  • Для найденных собственных значений справедливо: [math]\lambda_i(T_{k+1})\geq \lambda_i(T_{k})\geq \lambda_{i+1}(T_{k+1})\geq \lambda_{i+1}(T_{k})[/math], т.е. в первую очередь находятся максимальные по модулю собственные значения.
  • Как следствие предыдущего пункта алгоритм Ланцоша особенно удобен для вычисления собственных значений матрицы, находящихся на границе ее спектра.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

3 Литература

  1. ↑ Деммель Д. Вычислительная линейная алгебра
  2. ↑ https://en.wikipedia.org/wiki/Divide-and-conquer_eigenvalue_algorithm
  3. ↑ Деммель Д. Вычислительная линейная алгебра
Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Shostix/Алгоритм_Ланцоша_для_точной_арифметики_(без_переортогонализации)&oldid=21705