Участник:Vid1525/Дерево отрезков

Алгоритм нахождения суммы чисел на отрезке с помощью одномерного "Дерево отрезков"
Последовательный алгоритм
Последовательная сложность	[math]O(qlog(n))[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]q[/math]

Автор: И.Д. Васенков

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Дерево отрезков - это упорядоченная древовидная структура данных для хранения списка точек. Эта структура позволяет эффективно сообщать результаты некоторых запросов на отрезках данного списка точек (например сумма / минимум) и обычно используется в двух или более измерениях. Деревья отрезков были введены Джоном Луисом Бентли в 1979 году. Аналогичные структуры данных были обнаружены независимо Лукером, Ли и Вонгом. Дерево отрезков является альтернативой дереву k-d. По сравнению с деревьями k-d, деревья отрезков обеспечивают более быстрое время запроса (в обозначении Big O) [math]O(log ^ dn)[/math], но худшее хранение [math]O(nlog^{d-1}n)[/math], где n - количество точек, сохраненных в дереве, d - размерность дерева. В данной работе будет рассматриваться одномерное дерево отрезков.

1.2 Математическое описание алгоритма

Формальная постановка задачи:

Дана последовательность чисел длины [math]n[/math], далее будем обозначать элементы этой последовательности как [math]a_{0}, a_{1}, ..., a_{n-1}[/math]. Элементы последовательности - некоторые вещественные числа.

Суммой на отрезке [math][l, r][/math] данной последовательности назовем такое число [math]S[/math], такое что [math]S = \sum_{i=l}^{r}a_{i}, 0 \leq l \leq r \lt n[/math].

Дано [math]q[/math] запросов суммы на отрезках [math][l_{i}, r_{i}][/math], [math]i = 1..q[/math], [math]i[/math] - индекс запроса. [math]0 \leq l_{i} \leq r_{i} \lt n[/math]

Необходимо:

По входной последовательности [math]a_{0}, a_{1}, ..., a_{n-1}[/math] и входным запросам вернуть последовательность [math]S_{1}, ..., S_{q}[/math] - последовательность сумм на отрезках, заданных в запросах.

Дерево отрезков позволяет выполнять операции получения суммы не за линейное время (за длину входного отрезка), а за время [math]O(log(n))[/math]. Такая скорость работы достигается за счет хранения информации о суммах на некоторых отрезках входной последовательности и благодаря процессу предобработки входной последовательности перед выполнением запросов (Подробная реализация предобработки и запросов описана в пункте 1.5).

1.3 Вычислительное ядро алгоритма

Зачастую основное время выполнение алгоритма занимают операции получения сумм на отрезках, так как операция построения дерева выполняется один раз, а количество запросов суммы может быть достаточно большим.

1.4 Макроструктура алгоритма

Основные операции алгоритма:

• Предобработка - заполение значений частичных сумм на подотрезках.
• Выполнение операции запроса суммы на отрезке.

1.5 Схема реализации последовательного алгоритма

Построение дерева:

• Cоздать массив [math]tree[/math] размера [math]2^{k+1}[/math] для хранения дерева отрезков, где [math]2^{k-1} \lt n \leq 2^{k} = m[/math], [math]k[/math] - натуральное число, [math]n[/math] - длина входного массива [math]a[/math] (массив [math]tree[/math] для удобства инициализируется нулевыми значениями)
• Перенести значения сходного массива [math]a[/math] в массив [math]tree[/math] следующим образом: [math]tree[m+i] = a[i], i = 0..n-1[/math]
• Произвести операцию инициализации значений на более высоких уровнях дерева:

for (i = m - 1; i > 0; --i)
    tree[i] = tree[i * 2] + tree[i * 2 + 1];

• Таким образом получим массив tree, в котором хранятся значения некоторых сумм для исходного массива (например сумма всех значений исходного массива хранится в элементе tree[1]).

Запрос суммы на отрезке:

• На вход поступают два числа [math]l[/math] и [math]r[/math] - границы отрезка, необходимо посчитать сумму на отрезке [math]a[l .. r][/math].

• Для этого мы будем спускаться по построенному дереву отрезков, используя для подсчёта ответа посчитанные ранее суммы на каждой вершине дерева. Изначально мы встаём в корень дерева отрезков. Посмотрим, в какие из двух его сыновей попадает отрезок запроса [math][l .. r][/math] (напомним, что сыновья корня дерева отрезков — это отрезки [math][0 .. n/2][/math] и [math][n/2+1 .. n-1][/math]). Возможны два варианта: что отрезок [math][l..r][/math] попадает только в одного сына корня, и что, наоборот, отрезок пересекается с обоими сыновьями.

• В первом случае: перейдём в того сына, в котором лежит наш отрезок-запрос, и применим описываемый здесь алгоритм к текущей вершине.

• Во втором же случае нам не остаётся других вариантов, кроме как перейти сначала в левого сына и посчитать ответ на запрос в нём, а затем — перейти в правого сына, посчитать в нём ответ и прибавить к нашему ответу. Иными словами, если левый сын представлял отрезок [math][l_1 .. r_1][/math], а правый — отрезок [math][l_2 .. r_2][/math] (заметим, что [math]l_2 = r_1 + 1[/math]), то мы перейдём в левого сына с запросом [math][l .. r_1][/math], а в правого — с запросом [math][l_2 .. r][/math].

Таким образом после завершения первого вызова данной фукнции можно получить сумму на отрезке [math][l, r][/math].

1.6 Последовательная сложность алгоритма

• Построение дерева:

Для длины увеличенного массива m (m - степень двойки) справедлива оценка сверху [math]m \lt 2n[/math] (худший случай, когда исходная длина массива была [math]n = 2^{k}+1[/math], тогда нужно добавить в конец исходного массива [math]2^{k} - 1[/math] элементов). При построении дерева необходимо хранить суммы на подотрезках, но так как дерево отрезков имеет структуру полного бинарного дерева, а нижний уровень содержит m вершин, то всего в дереве не более 2m узлов, при этом каждый узел заполняется только один раз). Следовательно на предобработку необходимо [math]O(n)[/math] операций.

• Запрос суммы на отрезке:

При запросе суммы необходимо спускаться вниз по дереву, утверждается, что на каждом уровне дерева алгоритм посетит не более 4 вершин, учитывая оценку на высоту дерева отрезков - [math]O(log(n))[/math], получаем оценку на выполнение операции - [math]O(log(n))[/math].

1.7 Информационный граф

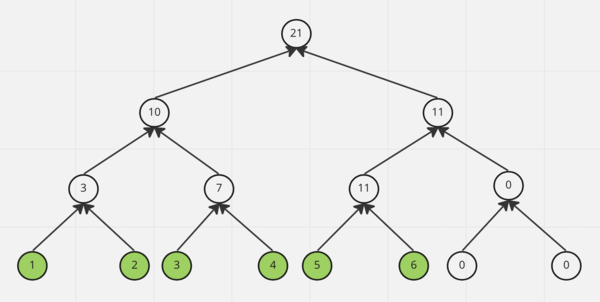
Пример построения дерева отрезков для массива длины n = 6, a = [1, 2, 3, 4, 5, 6] (зеленые вершины - элементы исходного массива в дереве).

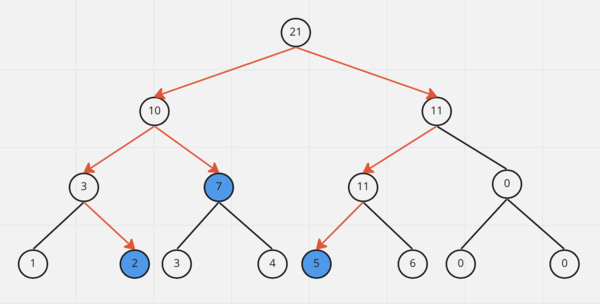
Пример запроса суммы на отрезке [1..4] для массива из предыдущего примера (красные стрелки показывают, переходы между вершинами при выполнении функции запроса, синие вершины - вершины, из которых были взяты значения для суммирования на отрезке).

1.8 Ресурс параллелизма алгоритма

При отсутствии изменяющих запросов в дереве отрезков можно считать, что все запросы к дереву могут быть выполнены параллельно (если количество потоков выполнения запросов не ограничено). При построении дерева необходимо учитывать, что более высокие слои дерева невозможно построить без предыдущих более низких слоев, поэтому строить дерево лучше всего снизу вверх (запускать несколько потоков суммирования значений на одном уровне, после чего переходить к следующему).

1.9 Входные и выходные данные алгоритма

Входные данные: - Массив чисел длины n (в данном примере считаем, что элементы массива - 64-битные целые беззнаковые числа, суммирование происходит по модулю [math]2^{64}[/math])

- q запросов, каждый из которых состоит из пары чисел [math]l_{i}[/math] и [math]r_{i}, l_{i}, r_{i} \in [0, n-1][/math] и [math]l \leq r[/math]; числа l и r задают границы отрезка, на котором будет происходить суммирование чисел (индексация массива начинается с нуля, [math]i = 1, ..., q[/math] - номер запроса)

Выходные данные: - Массив сумм на отрезках [math][l_{i}, r_{i}], i = 1, ..., q[/math] (размер массива - q)

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

Sqlite https://www.sqlite.org/

SciPy https://scipy.org/

Sklearn https://scikit-learn.org/stable/

3 Литература

1. Bentley, J. L. (1979). "Decomposable searching problems".

2. Lueker, G. S. (1978). "A data structure for orthogonal range queries". 19th Annual Symposium on Foundations of Computer Science (sfcs 1978).

3. Lee, D. T.; Wong, C. K. (1980). "Quintary trees: A file structure for multidimensional database systems". ACM Transactions on Database Systems.