Участник:Yastrebovks/Алгоритм Ланцоша с полной переортогонализацией: различия между версиями
ASA (обсуждение | вклад) |
|||
| (не показано 30 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | {{Assignment|ASA}} | ||
| + | |||
{{algorithm | {{algorithm | ||
| name = Алгоритм Ланцоша с полной переортогонализацией | | name = Алгоритм Ланцоша с полной переортогонализацией | ||
| Строка 8: | Строка 10: | ||
Авторы: Алексейчук Н.Н 616, Ястребов К.С. 609. | Авторы: Алексейчук Н.Н 616, Ястребов К.С. 609. | ||
| + | Авторы внесли равнозначный вклад в каждый из разделов данной статьи. | ||
| − | == Общее описание алгоритма. == | + | ==Свойства и структура алгоритма == |
| + | === Общее описание алгоритма. === | ||
Алгоритм Ланцоша ищет собвственные значения и собственные векторы для симетричной матрицы A вещественных чисел. Является итерацонным алгоритмом. Алгоритм Ланцоша использует степенной метод (<math> b_{k+1} = \frac{Ab_k}{||Ab_k||} </math>) для поиска наибольших собственных значений и векторов матриц. | Алгоритм Ланцоша ищет собвственные значения и собственные векторы для симетричной матрицы A вещественных чисел. Является итерацонным алгоритмом. Алгоритм Ланцоша использует степенной метод (<math> b_{k+1} = \frac{Ab_k}{||Ab_k||} </math>) для поиска наибольших собственных значений и векторов матриц. | ||
| Строка 18: | Строка 22: | ||
| − | == Математическое описание алгоритма == | + | === Математическое описание алгоритма === |
Памятка: | Памятка: | ||
| Строка 30: | Строка 34: | ||
В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности <math>n</math>X<math>n</math>: <math>A=A^T</math>; а так же вектор начального приближения <math>b</math>. | В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности <math>n</math>X<math>n</math>: <math>A=A^T</math>; а так же вектор начального приближения <math>b</math>. | ||
| − | Метод осуществляет поиск трехдиагональной симметричной матрицы <math>T_k=Q_k^TAQ_k</math>. Причем собственные значения <math>T_k</math> таковы, что приближают собственные значения исходной матрицы <math>A</math>. То есть на каждом <math>k</math>-м шаге из ортонормированных векторов Ланцоша строится матрица <math>Q_k = [q_1,q_2,...,q_k]</math> и в качестве приближенных собственных значений матрицы <math>A</math> принимаются числа Ритца. | + | Метод осуществляет поиск трехдиагональной симметричной матрицы <math>T_k=Q_k^TAQ_k</math>. |
| + | |||
| + | Таким образом матрица <math>T_k=\begin{bmatrix} | ||
| + | \alpha_1 & \beta_2 \\ | ||
| + | \beta_2 & \alpha_2 & \beta_3 &\\ | ||
| + | &. & . & .\\ | ||
| + | &&\beta_{k-1} & \alpha_{k-1} & \beta_k\\ | ||
| + | &&&\beta_k & \alpha_k | ||
| + | |||
| + | \end{bmatrix}</math> | ||
| + | |||
| + | Причем собственные значения <math>T_k</math> таковы, что приближают собственные значения исходной матрицы <math>A</math>. То есть на каждом <math>k</math>-м шаге из ортонормированных векторов Ланцоша строится матрица <math>Q_k = [q_1,q_2,...,q_k]</math> и в качестве приближенных собственных значений матрицы <math>A</math> принимаются числа Ритца. | ||
Из-за ошибок округления вектора <math> A^{k-1}x_1 </math>, формирующие подпространство Крылова, становятся неортогональными. Чтобы решить данную прорблему, проводят переортогонализацию методом Грамма-Шмидта. | Из-за ошибок округления вектора <math> A^{k-1}x_1 </math>, формирующие подпространство Крылова, становятся неортогональными. Чтобы решить данную прорблему, проводят переортогонализацию методом Грамма-Шмидта. | ||
| − | == Вычислительное ядро алгоритма == | + | === Вычислительное ядро алгоритма === |
Вычислительным ядром данного алгоритма являются следующие шаги: | Вычислительным ядром данного алгоритма являются следующие шаги: | ||
| Строка 43: | Строка 58: | ||
В данном случае первая операция выполняет умножение симметричной матрицы <math>A</math> размерности <math>n</math>X<math>n</math> на <math>n</math>-мерный вектор <math>q</math>, вследствие чего вычислительная сложность выполнения заключается в <math>n^2</math> умножений и <math>n^2-n</math> сложений. Второе действие является процессом ортогонализации Грама-Шмидта. В последнем действии вычисляются <math>k^2n+k(n+2)</math> умножений и <math>k^2n + k(n + 1) + 2</math> операций сложения. | В данном случае первая операция выполняет умножение симметричной матрицы <math>A</math> размерности <math>n</math>X<math>n</math> на <math>n</math>-мерный вектор <math>q</math>, вследствие чего вычислительная сложность выполнения заключается в <math>n^2</math> умножений и <math>n^2-n</math> сложений. Второе действие является процессом ортогонализации Грама-Шмидта. В последнем действии вычисляются <math>k^2n+k(n+2)</math> умножений и <math>k^2n + k(n + 1) + 2</math> операций сложения. | ||
| − | == Макроструктура алгоритма == | + | === Макроструктура алгоритма === |
| − | *1. | + | Основные операции: |
| + | *1. Умножение матрицы на вектор. | ||
| + | <math>b=Ax</math>. | ||
| + | |||
| + | *2. Двойная ортогонализация методом Грмма-Шмидта. | ||
| + | <math>z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i,</math> | ||
| + | |||
| + | |||
| + | <math>z=z-\alpha_jq_j-\beta_{j}q_{j-1}.</math> | ||
| + | |||
| + | *3. Вычисление нового базисного вектора. | ||
| + | <math>q_{i+1} = z/ \beta</math>. | ||
| + | |||
| + | |||
| + | === Схема реализации последовательного алгоритма === | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \mathtt{input:}\; A, b, k\\ | ||
| + | q_1 = b / \Vert b \Vert_2\\ | ||
| + | Q = q_1\\ | ||
| + | \mathtt{for}\; j = \overline{1, k}:\\ | ||
| + | \quad z = A q_j \\ | ||
| + | \quad \alpha_j = q_j^T z \\ | ||
| + | \quad z = z - Q \left( Q^T z \right) \\ | ||
| + | \quad z = z - Q \left( Q^T z \right)\\ | ||
| + | \quad \beta_j = \Vert z \Vert_2\\ | ||
| + | \quad \mathtt{if }\; \beta_j = 0\\ | ||
| + | \quad \quad \mathtt{exit}\\ | ||
| + | \quad \mathtt{end \; if}\\ | ||
| + | \quad q_{j+1} = z/\beta_j\\ | ||
| + | \quad Q = [Q, q_{j + 1}]\\ | ||
| + | \mathtt{end \; for}\\ | ||
| + | \mathtt{output:}\; [\alpha_1, \dots, \alpha_k], [\beta_1, \dots, \beta_{k - 1}], [q_1, \dots, q_k]. | ||
| + | \end{array} | ||
| + | </math> | ||
| − | + | Рассмотрим подробнее все шаги данного алгоритма: | |
| + | <math> | ||
| + | 1.z=Aq_j, | ||
| + | </math> | ||
| − | + | Вычисляется диагональный элемент конечной матрицы <math>T_k</math>, | |
| − | |||
| − | |||
| − | + | <math> | |
| − | + | 2.\alpha_j=q_j^Tz, | |
| − | + | </math> | |
| − | |||
| − | |||
| − | \alpha_j | ||
| − | |||
| − | |||
| − | |||
| + | Далее дважды проводится полная переортогонализация по Грамму-Шмидту. Данные действия необходимы для гарантии ортогональности базиса. | ||
| − | \ | + | <math> |
| + | 3.z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, </math> | ||
| + | |||
| + | <math>4.z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, </math> | ||
| + | |||
| + | <math>5.z=z-\alpha_jq_j-\beta_{j}q_{j-1}, </math> | ||
| + | |||
| + | Далее вычисляются недостающие элементы матрицы <math>T_k</math>. | ||
| + | |||
| + | <math>6.\beta_{j+1}=||z||, | ||
</math> | </math> | ||
| − | == Последовательная сложность алгоритма== | + | Если <math>\beta_{j+1}=0</math>, то алгоритм завершается. |
| + | |||
| + | <math>7.q_{j+1}=z/\beta_{j+1}.</math> | ||
| + | |||
| + | В конце каждой итерации получаем очередной вектор <math>q_{j+1}</math> базиса с единичной нормой, который ортогонален всем предыдущим векторам базиса, | ||
| + | |||
| + | и элементы <math>\alpha_j</math>, <math>\beta_{j+1}</math> трехдиагональной матрицы <math>T_k</math> . | ||
| + | |||
| + | Кроме того, заметим, что очень часто в макрооперациях возникает операция вычисления суммы всех элементов массива. Её необходимо выполнять и при умножении матрицы на вектор, и при вычислении скалярного произведения, и при вычислении нормы вектора. Разные методы суммирования дают разный ресурс параллелизма. В этой работе предполагается, что везде для суммирования используется последовательный способ. | ||
| + | |||
| + | === Последовательная сложность алгоритма === | ||
Количество операций складывается из количества операций для классического метода Ланцоша[https://books.google.ru/books?id=T8EPBwAAQBAJ&pg=PA242&lpg=PA242&dq=lanczos+algorithm+complexity&source=bl&ots=kWVnVP_uJp&sig=a-4GTEt6vRE8YhR1R6dOPwvOSIk&hl=en&sa=X&ved=0ahUKEwiQ2u3U4-LPAhWvbZoKHe0QBaw4ChDoAQg7MAY#v=onepage&q=lanczos%20algorithm%20complexity&f=false] и количества операций для переортогонализации методом грамма-Шмидта[http://stackoverflow.com/questions/27986225/computational-complexity-of-gram-schmidt-orthogonalization-algorithm]. | Количество операций складывается из количества операций для классического метода Ланцоша[https://books.google.ru/books?id=T8EPBwAAQBAJ&pg=PA242&lpg=PA242&dq=lanczos+algorithm+complexity&source=bl&ots=kWVnVP_uJp&sig=a-4GTEt6vRE8YhR1R6dOPwvOSIk&hl=en&sa=X&ved=0ahUKEwiQ2u3U4-LPAhWvbZoKHe0QBaw4ChDoAQg7MAY#v=onepage&q=lanczos%20algorithm%20complexity&f=false] и количества операций для переортогонализации методом грамма-Шмидта[http://stackoverflow.com/questions/27986225/computational-complexity-of-gram-schmidt-orthogonalization-algorithm]. | ||
Итоговая сложность составляет <math>O(n^2)+O(nk^2) </math>. | Итоговая сложность составляет <math>O(n^2)+O(nk^2) </math>. | ||
| − | == Информационный граф == | + | === Информационный граф === |
| − | [[Файл: | + | [[Файл:LanzochGraph.png]] |
| − | == Входные и выходные данные алгоритма == | + | Троеточием в данном алгоритме обозначаются операции, выполняющиеся для всех элементов от <math>i=1..n</math>. |
| + | |||
| + | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | Хотя алгоритм является итерационным, возможно распараллелить внутри каждой итерации умножение матрицы на вектор и процесс переортогонализации Грамма-Шмидта. | ||
| + | |||
| + | Процесс умножения матриц matvec можно распараллелить несколькими способами[https://eprint.iacr.org/2011/416.pdf]. | ||
| + | |||
| + | Как видно из графа, для выполнения j-й операции, необходимо выполнить следующие ярусы: | ||
| + | # <math>n</math> ярусов сложений с <math>n</math> операциями умножения в каждом (вычисление <math>z</math>); | ||
| + | # <math>n</math> ярусов сложений с <math>1</math> операцией умножения в каждом (вычисление <math>\alpha_j</math>); | ||
| + | # <math>j</math> ярусов сложений с <math>n</math> операциями умножения в каждом, <math>n</math> ярусов сложений с <math>j</math> операциями умножения в каждом, <math>1</math> ярус вычитаний размера <math>n</math> (первая переортогонализация); | ||
| + | # <math>j</math> ярусов сложений с <math>n</math> операциями умножения в каждом, <math>n</math> ярусов сложений с <math>j</math> операциями умножения в каждом, <math>1</math> ярус вычитаний размера <math>n</math> (вторая переортогонализация); | ||
| + | # <math>n</math> ярусов сложений с <math>1</math> операцией умножения в каждом (вычисление <math>\beta_j</math>); | ||
| + | # <math>1</math> ярус делений размера <math>n</math> (вычисление <math>q_{j + 1}</math>). | ||
| + | |||
| + | Если учесть весь ресурс параллелизма, можно получить мультипликативную вычислительную сложность всего алгоритма: <math>O(n^2k+nk^2)/p)</math>. | ||
| + | |||
| + | Вычислительная мощность данного алгоритма, как отношение числа операций к суммарному объему входных и выходных, данных равняется <math>O(k)</math>. | ||
| + | |||
| + | === Входные и выходные данные алгоритма === | ||
На вход принимается сама матрица <math> A \in R^{n \times n}</math>, случайный вектор <math>b</math> (впрочем возможен вариант, при котором этот вектор генерируется случайным образом). | На вход принимается сама матрица <math> A \in R^{n \times n}</math>, случайный вектор <math>b</math> (впрочем возможен вариант, при котором этот вектор генерируется случайным образом). | ||
Ввиду симметричности входной матрицы достаточно передать лишь ее верхнюю треугольную матрицу, что дает объем входных данных <math>\frac{n(n + 1)}{2}</math>. | Ввиду симметричности входной матрицы достаточно передать лишь ее верхнюю треугольную матрицу, что дает объем входных данных <math>\frac{n(n + 1)}{2}</math>. | ||
| Строка 84: | Строка 168: | ||
Выходными данными для <math>j</math>ой итерации являются вектор <math> Aq_j </math> и собственное число <math> \lambda </math>. Общий объем выходных данных <math>k(n+1)</math>. | Выходными данными для <math>j</math>ой итерации являются вектор <math> Aq_j </math> и собственное число <math> \lambda </math>. Общий объем выходных данных <math>k(n+1)</math>. | ||
| − | ==Свойства алгоритма== | + | === Свойства алгоритма === |
Если <math>A</math> эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам ритца[http://ta.twi.tudelft.nl/nw/users/vuik/papers/DUT-TWI-96-44.pdf]. | Если <math>A</math> эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам ритца[http://ta.twi.tudelft.nl/nw/users/vuik/papers/DUT-TWI-96-44.pdf]. | ||
| Строка 91: | Строка 175: | ||
Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым. | Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым. | ||
| − | |||
| − | + | == Программная реализация алгоритма == | |
| + | |||
| + | |||
| + | === Особенности реализации последовательного алгоритма === | ||
| + | === Локальность данных и вычислений === | ||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
| + | === Масштабируемость алгоритма и его реализации === | ||
| + | Исследование масштабируемости реализации алгоритма проводилось с использованием стандарта MPI на суперкомпьютере "Ломоносов". | ||
| + | |||
| + | Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма: | ||
| + | *Число процессоров <math>4,8,16,32,64,128</math> | ||
| + | *Размерность матрицы <math> 10000,15000, 20000,25000,30000,35000, 40000, 45000, 50000</math> | ||
| + | *Количество итераций <math>44</math> | ||
| + | Сборка осуществлялась с параметрами: | ||
| + | *openmpi/1.5.5-icc | ||
| + | *intel/13.1.0 | ||
| + | |||
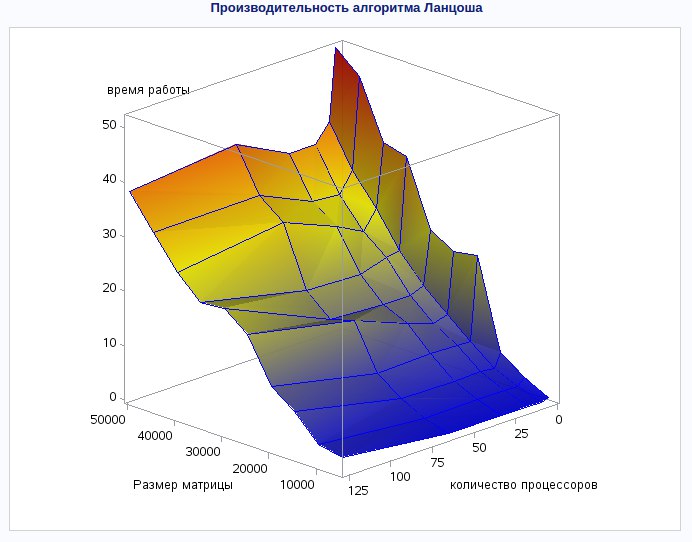
| + | [[Файл:LanzochFigure1.jpg]] | ||
| + | |||
| + | [http://pastebin.com/qX26e3WU Используемая параллельная реализация алгоритма на языке C++] | ||
| − | |||
| + | На данном графике отчетливо видно, что время выполнения алгоритма сильно уменьшается с увеличением количества процессов при расчете матрицы любой размерности. При этом наблюдается некоторое снижение производительности в случае наибольших размеров матриц. Данный факт является следствием большого количества данных, необходимого для обмена между процессами. Отсюда опытным путем можно установить, что наибольшая производительность алгоритма будет достигнута, если размерность матрицы не будет превышать 30000-35000. | ||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | === Выводы для классов архитектур === | ||
| − | == | + | === Существующие реализации алгоритма === |
The IETL Project http://www.comp-phys.org/software/ietl/ C++ | The IETL Project http://www.comp-phys.org/software/ietl/ C++ | ||
Текущая версия на 11:24, 8 декабря 2016
 | Эта работа прошла предварительную проверку Дата последней правки страницы: 08.12.2016 Данная работа соответствует формальным критериям. Проверено ASA. |
| Алгоритм Ланцоша с полной переортогонализацией | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^2)+O(nk^2) [/math] |
| Объём входных данных | [math]\frac{n(n + 1)}{2}[/math] |
| Объём выходных данных | [math]k(n + 1)[/math] |
Авторы: Алексейчук Н.Н 616, Ястребов К.С. 609. Авторы внесли равнозначный вклад в каждый из разделов данной статьи.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма.
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма.
Алгоритм Ланцоша ищет собвственные значения и собственные векторы для симетричной матрицы A вещественных чисел. Является итерацонным алгоритмом. Алгоритм Ланцоша использует степенной метод ([math] b_{k+1} = \frac{Ab_k}{||Ab_k||} [/math]) для поиска наибольших собственных значений и векторов матриц.
В отличие от прямых алгоритмов требует мешьше памяти и мощности, что является несомненным плюсом для больших матриц.
Несмотря на свою скорость работы и экономию памяти, сначала не был популярным алгоритмом из – за недостаточной вычислительной устойчивости. В 1970 году Ojalvo и Newman [1] показали способ сделать алгоритм достаточно устойчивым. В этой же статье алгоритм был применен к расчету инженерной конструкции с большим количеством узлов, которые подвергались динамической нагрузке.
1.2 Математическое описание алгоритма
Памятка: Степенной метод нахождения наибольшего собственного числа матрицы можно сформулировать в предельном виде: если [math] b_0 [/math] – случайный вектор, и [math] b_n+1 = Ab_n [/math], тогда для больших чисел n предел [math]x_n/||x_n|| [/math] стремится к нормированному наибольшему собственному вектору.
Алгоритм Ланцоша комбинирует метод Ланцоша для нахождения крыловского подпространства и метод Релэя – Ритца.
Подпространство Крылова для степенного метода: [math] K_m(v,A) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] [/math]
В качестве входных данных для алгоритма Ланцоша подаются квадратная матрица размерности [math]n[/math]X[math]n[/math]: [math]A=A^T[/math]; а так же вектор начального приближения [math]b[/math].
Метод осуществляет поиск трехдиагональной симметричной матрицы [math]T_k=Q_k^TAQ_k[/math].
Таким образом матрица [math]T_k=\begin{bmatrix} \alpha_1 & \beta_2 \\ \beta_2 & \alpha_2 & \beta_3 &\\ &. & . & .\\ &&\beta_{k-1} & \alpha_{k-1} & \beta_k\\ &&&\beta_k & \alpha_k \end{bmatrix}[/math]
Причем собственные значения [math]T_k[/math] таковы, что приближают собственные значения исходной матрицы [math]A[/math]. То есть на каждом [math]k[/math]-м шаге из ортонормированных векторов Ланцоша строится матрица [math]Q_k = [q_1,q_2,...,q_k][/math] и в качестве приближенных собственных значений матрицы [math]A[/math] принимаются числа Ритца.
Из-за ошибок округления вектора [math] A^{k-1}x_1 [/math], формирующие подпространство Крылова, становятся неортогональными. Чтобы решить данную прорблему, проводят переортогонализацию методом Грамма-Шмидта.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром данного алгоритма являются следующие шаги:
- 1. [math]Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)[/math].
- 2. [math]z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i.[/math]
В данном случае первая операция выполняет умножение симметричной матрицы [math]A[/math] размерности [math]n[/math]X[math]n[/math] на [math]n[/math]-мерный вектор [math]q[/math], вследствие чего вычислительная сложность выполнения заключается в [math]n^2[/math] умножений и [math]n^2-n[/math] сложений. Второе действие является процессом ортогонализации Грама-Шмидта. В последнем действии вычисляются [math]k^2n+k(n+2)[/math] умножений и [math]k^2n + k(n + 1) + 2[/math] операций сложения.
1.4 Макроструктура алгоритма
Основные операции:
- 1. Умножение матрицы на вектор.
[math]b=Ax[/math].
- 2. Двойная ортогонализация методом Грмма-Шмидта.
[math]z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i,[/math]
[math]z=z-\alpha_jq_j-\beta_{j}q_{j-1}.[/math]
- 3. Вычисление нового базисного вектора.
[math]q_{i+1} = z/ \beta[/math].
1.5 Схема реализации последовательного алгоритма
[math] \begin{array}{l} \mathtt{input:}\; A, b, k\\ q_1 = b / \Vert b \Vert_2\\ Q = q_1\\ \mathtt{for}\; j = \overline{1, k}:\\ \quad z = A q_j \\ \quad \alpha_j = q_j^T z \\ \quad z = z - Q \left( Q^T z \right) \\ \quad z = z - Q \left( Q^T z \right)\\ \quad \beta_j = \Vert z \Vert_2\\ \quad \mathtt{if }\; \beta_j = 0\\ \quad \quad \mathtt{exit}\\ \quad \mathtt{end \; if}\\ \quad q_{j+1} = z/\beta_j\\ \quad Q = [Q, q_{j + 1}]\\ \mathtt{end \; for}\\ \mathtt{output:}\; [\alpha_1, \dots, \alpha_k], [\beta_1, \dots, \beta_{k - 1}], [q_1, \dots, q_k]. \end{array} [/math]
Рассмотрим подробнее все шаги данного алгоритма:
[math] 1.z=Aq_j, [/math]
Вычисляется диагональный элемент конечной матрицы [math]T_k[/math],
[math] 2.\alpha_j=q_j^Tz, [/math]
Далее дважды проводится полная переортогонализация по Грамму-Шмидту. Данные действия необходимы для гарантии ортогональности базиса.
[math] 3.z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]
[math]4.z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i, [/math]
[math]5.z=z-\alpha_jq_j-\beta_{j}q_{j-1}, [/math]
Далее вычисляются недостающие элементы матрицы [math]T_k[/math].
[math]6.\beta_{j+1}=||z||, [/math]
Если [math]\beta_{j+1}=0[/math], то алгоритм завершается.
[math]7.q_{j+1}=z/\beta_{j+1}.[/math]
В конце каждой итерации получаем очередной вектор [math]q_{j+1}[/math] базиса с единичной нормой, который ортогонален всем предыдущим векторам базиса,
и элементы [math]\alpha_j[/math], [math]\beta_{j+1}[/math] трехдиагональной матрицы [math]T_k[/math] .
Кроме того, заметим, что очень часто в макрооперациях возникает операция вычисления суммы всех элементов массива. Её необходимо выполнять и при умножении матрицы на вектор, и при вычислении скалярного произведения, и при вычислении нормы вектора. Разные методы суммирования дают разный ресурс параллелизма. В этой работе предполагается, что везде для суммирования используется последовательный способ.
1.6 Последовательная сложность алгоритма
Количество операций складывается из количества операций для классического метода Ланцоша[2] и количества операций для переортогонализации методом грамма-Шмидта[3].
Итоговая сложность составляет [math]O(n^2)+O(nk^2) [/math].
1.7 Информационный граф
Троеточием в данном алгоритме обозначаются операции, выполняющиеся для всех элементов от [math]i=1..n[/math].
1.8 Ресурс параллелизма алгоритма
Хотя алгоритм является итерационным, возможно распараллелить внутри каждой итерации умножение матрицы на вектор и процесс переортогонализации Грамма-Шмидта.
Процесс умножения матриц matvec можно распараллелить несколькими способами[4].
Как видно из графа, для выполнения j-й операции, необходимо выполнить следующие ярусы:
- [math]n[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом (вычисление [math]z[/math]);
- [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\alpha_j[/math]);
- [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (первая переортогонализация);
- [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом, [math]1[/math] ярус вычитаний размера [math]n[/math] (вторая переортогонализация);
- [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом (вычисление [math]\beta_j[/math]);
- [math]1[/math] ярус делений размера [math]n[/math] (вычисление [math]q_{j + 1}[/math]).
Если учесть весь ресурс параллелизма, можно получить мультипликативную вычислительную сложность всего алгоритма: [math]O(n^2k+nk^2)/p)[/math].
Вычислительная мощность данного алгоритма, как отношение числа операций к суммарному объему входных и выходных, данных равняется [math]O(k)[/math].
1.9 Входные и выходные данные алгоритма
На вход принимается сама матрица [math] A \in R^{n \times n}[/math], случайный вектор [math]b[/math] (впрочем возможен вариант, при котором этот вектор генерируется случайным образом). Ввиду симметричности входной матрицы достаточно передать лишь ее верхнюю треугольную матрицу, что дает объем входных данных [math]\frac{n(n + 1)}{2}[/math].
Выходными данными для [math]j[/math]ой итерации являются вектор [math] Aq_j [/math] и собственное число [math] \lambda [/math]. Общий объем выходных данных [math]k(n+1)[/math].
1.10 Свойства алгоритма
Если [math]A[/math] эрмитова матрица, то алгоритм Ланцоша и Bi-Lanczos сходятся к одинаковым трехдиагональным матрицам ритца[5].
При реализации классического алгоритма Ланцоша возникает большая погрешность при округлении. Вариант с полной переортогонализацией позволяет избегать больших погрешностей, однако является более ресурсоемким. Существует промежуточный вариант с частичной переортогонализацией.
Алгоритм может завершить свою работу досрочно, когда найденные собственные значения будут достаточно близки к целевым.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование масштабируемости реализации алгоритма проводилось с использованием стандарта MPI на суперкомпьютере "Ломоносов".
Набор изменяемых параметров запуска реализации алгоритма и границы значений параметров алгоритма:
- Число процессоров [math]4,8,16,32,64,128[/math]
- Размерность матрицы [math] 10000,15000, 20000,25000,30000,35000, 40000, 45000, 50000[/math]
- Количество итераций [math]44[/math]
Сборка осуществлялась с параметрами:
- openmpi/1.5.5-icc
- intel/13.1.0
Используемая параллельная реализация алгоритма на языке C++
На данном графике отчетливо видно, что время выполнения алгоритма сильно уменьшается с увеличением количества процессов при расчете матрицы любой размерности. При этом наблюдается некоторое снижение производительности в случае наибольших размеров матриц. Данный факт является следствием большого количества данных, необходимого для обмена между процессами. Отсюда опытным путем можно установить, что наибольшая производительность алгоритма будет достигнута, если размерность матрицы не будет превышать 30000-35000.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
The IETL Project http://www.comp-phys.org/software/ietl/ C++
NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R
ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB
GrapLab https://turi.com/products/create/open_source.html C++
С частичной переортаганализацией
LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran (уже распараллелена)
3 Литература
Ojalvo, I.U. and Newman, M., "Vibration modes of large structures by an automatic matrix-reduction method", AIAA J., 8 (7), 1234–1239 (1970).