Difference between revisions of "Horners method"
| [unchecked revision] | [unchecked revision] |
| Line 103: | Line 103: | ||
</source> | </source> | ||
| − | === | + | === Locality of data and computations === |
| − | ==== | + | ==== Locality of the algorithm’s implementation ==== |
| − | ===== | + | ===== Structure of memory access and a qualitative estimation of locality ===== |
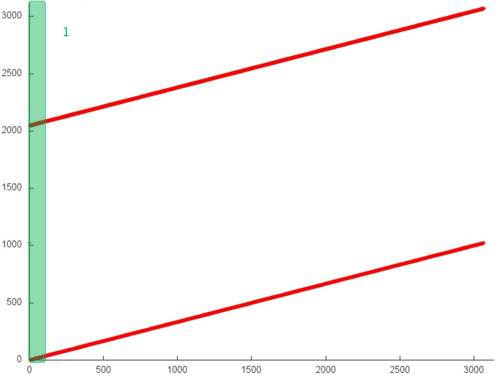
| − | [[file:Gorner_1.png|thumb|center|500px| | + | [[file:Gorner_1.png|thumb|center|500px|Fig. 2. Implementation of Horner’s scheme. The general memory-access profile.]] |
| − | + | The memory-access profile is illustrated in Fig. 2 for a sequential implementation of Horner’s scheme in the case of polynomials with real coefficients. From this figure it follows that the structure of this profile is very simple and consists of two linear (or sequential) searches of elements performed for two real arrays in parallel. | |
| − | + | However, this simple example shows that, in order to completely understand a general structure of memory access, it is necessary to carefully analyze this structure at the level of individual memory references. Figure 3 illustrates fragment 1 highlighted in green in Fig.2. As can be seen, the upper sequential search is somewhat different from the lower one: in the first case, each element is referenced twice in succession. Note, however, this refinement of the memory-access profile structure has a little effect on the locality of the entire profile. | |
| − | + | On the whole, the general memory-access profile possesses a high spatial locality, since the search of elements in the arrays is performed sequentially. However, the temporal locality is very low, since each element of one of the arrays is referenced only twice, whereas the elements of the second array are not reused at all. | |
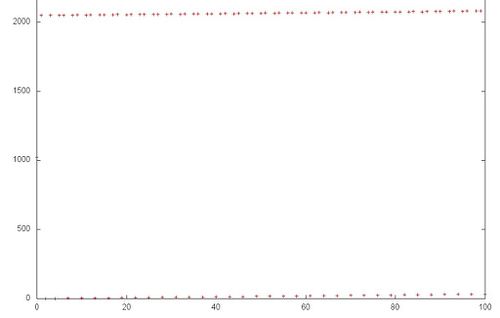
| − | [[file:Gorner_2.jpg|thumb|center|500px| | + | [[file:Gorner_2.jpg|thumb|center|500px|Fig 3. Fragment 1 (the first 100 references of the general profile).]] |
| − | ===== | + | ===== Quantitative estimation of locality ===== |
| − | + | The main fragment of the implementation used to obtain the quantitative estimates is given [http://git.algowiki-project.org/Voevodin/locality/blob/master/benchmarks/vectors/vectors.h here] (the KernelHorner function). The start conditions are discussed in [http://git.algowiki-project.org/Voevodin/locality/blob/master/README.md here]. | |
| − | + | The first estimate is made on the basis of the daps characteristic used to evaluate the number of write and read operations per second. This characteristic is similar to the flops estimate for memory access and is an estimate of the memory usage performance rather than an estimate of locality. However, the daps characteristic is a good information source and can be used to compare with the results obtained according to the cvg characteristic. | |
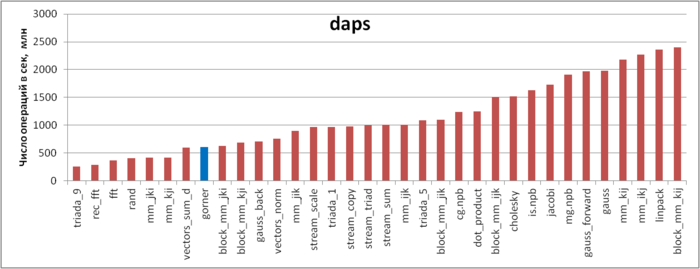
| − | + | Figure 4 illustrates the daps values for a number of some widespread algorithms. These values are given in increasing order: a higher performance corresponds to a larger daps value. From this figure it follows that the implementation of Horner’s scheme is characterized by a low memory usage performance. It may appear strange that in this case the daps value is significantly less than for the STREAM tests, although the memory-access profiles are similar: several simultaneous sequential searches for the elements of arrays. | |
| − | + | Such a behavior of the implementation under study is caused by the peculiarities of the memory structure. As mentioned above, the elements of one of the arrays are referenced twice in succession. In the source code of the implementation, however, the second reference is performed at the next iteration to the previous element:<source lang="c"> | |
| − | <source lang="c"> | ||
for (int i = 1; i < size; i++) { | for (int i = 1; i < size; i++) { | ||
c[i] = a[i] + c[i - 1] * x; | c[i] = a[i] + c[i - 1] * x; | ||
} | } | ||
</source> | </source> | ||
| − | + | Hence, we have the case when the iterations are dependent. As a result, the hardware prefetcher badly prefetches the required cache rows, which leads to a significant slowing of the program speed compared to the other implementations based on the sequential search (for example, the STREAM tests). | |
| − | + | Our discussion shows once more that the memory structure is very complex: a minor change made in the loop body leads to an expectedly serious slowing of the program. | |
[[file:Gorner_daps_ru.png|thumb|center|700px|Рисунок 12.3. Сравнение значений оценки daps]] | [[file:Gorner_daps_ru.png|thumb|center|700px|Рисунок 12.3. Сравнение значений оценки daps]] | ||
| − | + | The cvg characteristic is used to obtain a more machine-independent estimate of locality and to specify the frequency of fetching data to the cache memory. A lesser cvg value corresponds to a higher level of locality and to a smaller number of using the fetching procedure. | |
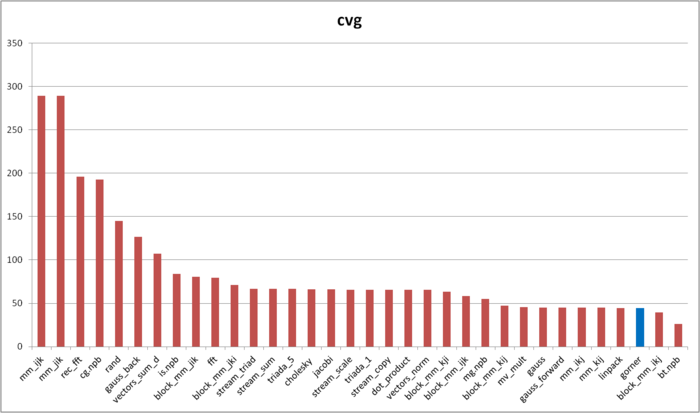
| − | + | Figure 5 shows the cvg values for the same implementations presented in Fig. 4. These values are given in decreasing order: a higher locality level corresponds to a smaller cvg value. From this figure it follows that the implementation of Horner’s scheme possesses a very high locality according to the cvg estimate. | |
| − | [[file:Gorner_cvg.png|thumb|center|700px| | + | [[file:Gorner_cvg.png|thumb|center|700px|Fig. 5. Comparison of cvg values.]] |
| − | + | As shown above, this conclusion does not correspond to the actual memory-access performance because of the peculiarities of the memory structure. However, it is necessary to state the following two remarks. First, the cases when the memory-access performance strongly depends on the hardware peculiarities of the memory structure are not very often in practice. Second, the cvg characteristic is used to obtain a machine-independent estimate of locality; hence, it is not possible to take into account such hardware peculiarities when the analysis of memory access is performed in the framework of complete machine independence. | |
| + | |||
| + | === Approaches and features of implementing Horner’s algorithm in parallel === | ||
| − | + | This algorithm is not designed to be implemented in parallel. | |
| − | + | === Scalability of Horner’s algorithm and its implementation === | |
| − | + | Scalability is not analyzed, since Horner’s algorithm is not designed to be implemented in parallel. | |
| − | |||
| − | |||
=== Динамические характеристики и эффективность реализации алгоритма === | === Динамические характеристики и эффективность реализации алгоритма === | ||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| − | === | + | === Existing implementations of Horner’s algorithm === |
| − | + | In addition to [[#Особенности реализации последовательного алгоритма|the above simplest implementation]], there exist more primitive codes implementing only a part of Horner’s scheme. This can be explained by the fact that in many cases it is necessary to know the value of a polynomial (the remainder of division), but it is not necessary to know only the quotient polynomial with the remainder dropped. In such cases one and the same scalar should be used instead of all the elements of the array <math>b</math>. | |
[[ru: Схема Горнера, вещественная версия, последовательный вариант]] | [[ru: Схема Горнера, вещественная версия, последовательный вариант]] | ||
[[Категория:Статьи в работе]] | [[Категория:Статьи в работе]] | ||
Revision as of 16:03, 24 May 2015
Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2)
Contents
- 1 Properties and structure of Horner’s scheme
- 1.1 Description of the algorithm
- 1.2 Mathematical description
- 1.3 The computational kernel of Horner’s algorithm
- 1.4 Macrostructure of the algorithm
- 1.5 Implementation of the sequential algorithm
- 1.6 Sequential complexity of the algorithm
- 1.7 Information graph
- 1.8 A parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Свойства алгоритма
- 2 Software implementation
- 2.1 Implementation peculiarities of the sequential algorithm
- 2.2 Locality of data and computations
- 2.3 Approaches and features of implementing Horner’s algorithm in parallel
- 2.4 Scalability of Horner’s algorithm and its implementation
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Existing implementations of Horner’s algorithm
1 Properties and structure of Horner’s scheme
1.1 Description of the algorithm
1.1.1 Formulation of the problem
Horner’s scheme is devoted to the division of a polynomial P_n(x) with known coefficients by the binomial x - \alpha. The results of this operation are the coefficients of the polynomial Q_{n - 1}(x) obtained by the relation
- P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)
and the value P_n(\alpha) of the polynomial P_n(x) at a given point \alpha.
Unfortunately, Horner’s method is often reduced only to the calculation of a polynomial P_n(x) at the point \alpha.
1.1.2 General scheme
Actually, Horner’s scheme implements the long division of a polynomial by the binomial x - \alpha. By the Bezout theorem, the remainder of this operation is equal to the value of a polynomial P_n(x) at a point \alpha.
1.2 Mathematical description
Input data: a one-dimensional array consisting of n + 1 numbers a_k and a scalar \alpha.
Output data: a one-dimensional array consisting of n + 1 numbers b_k.
The formulas of Horner's method are based on the relation
- P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x).
Now we represent the above polynomials in canonical form:
- \begin{align} P_n(x) & = a_0 x^n+ a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n, \\ Q_{n - 1}(x) & = b_0 x^{n - 1} + b_1 x^{n - 2} + \dots + b_{n - 2} x + b_{n - 1}. \end{align}
By b_n er denote P_n(\alpha). Substituting these polynomials in their canonical form into the above relation and equating the coefficients at equal powers of x, we come to the following formulas of Horner’s scheme:
- \begin{align} b_0 & = a_0, \\ b_k & = a_k + \alpha b_{k - 1}, \quad k = 1, \dots, n. \end{align}
1.3 The computational kernel of Horner’s algorithm
The computational kernel of Horner’s algorithm in its sequential version can be represented as a sequential set of n «double» operations: the multiplication of elements of the output array by one and the same scalar and the addition of the result to the next element of the input array.
1.4 Macrostructure of the algorithm
From the computational kernel of Horner’s algorithm it follows that its major part consists of the sequential set of the above «double» operations.
1.5 Implementation of the sequential algorithm
The formulas of the algorithm are described above. The operations are performed in increasing order of k.
1.6 Sequential complexity of the algorithm
For a polynomial of degree n, the number of multiplications is equal to n and the number of additions is also equal to n. Hence, Horner’s algorithm is of linear complexity with respect to the number of sequential operations.
1.7 Information graph
The graph of the algorithm is illustrated in Fig. 1 for n = 9. As can be seen, the graph is sequential.
Here the abbreviations In (Input) and Out (Output) are used to denote the first coefficient of the input array and the value of the polynomial at a given point \alpha, respectively. By Op we denote the "double" operation: the multiplication of an input variable by a scalar and the addition of the result to another variable.
1.8 A parallelization resource of the algorithm
The sequential version of Horner’s algorithm has no parallelization resource. Its parallel form consists of a single layer and is coincident with the sequential algorithm. Thus, the height of the parallel form is equal to n multiplications plus n additions. Hence, this algorithm is of linear complexity with respect to the height of the parallel form. The width of the parallel form is equal to 1; hence, this algorithm is of constant complexity with respect to the width of the parallel form.
1.9 Input and output data of the algorithm
Input data: an array a (its elements are denoted by a_i, where i = 0, \dots, n) and a scalar \alpha.
Additional constraints: absent.
Amount of input data: n + 2.
Output data: an array b (its elements are denoted by b_k, where k = 0, \dots, n)
Amount of output data:: n + 1.
1.10 Свойства алгоритма
In the case of unlimited computer resources, the ratio of the sequential complexity to the parallel complexity is constant (1). Computational power of the algorithm considered as the ratio of the number of operations to the total amount of input and output data is equal to 1 (the number of input and output data is even larger by 1 than the number of operations). The algorithm is completely deterministic. The arcs of the information graph are local. The stability of Horner’s scheme is optimal for the calculation of the values of a polynomial with known coefficient.
2 Software implementation
2.1 Implementation peculiarities of the sequential algorithm
Horner’s scheme can be represented in Fortran as
b(0) = a(0)
DO I = 1, N
b(I) = a(I)+b(I-1)*alpha
END DO
2.2 Locality of data and computations
2.2.1 Locality of the algorithm’s implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
The memory-access profile is illustrated in Fig. 2 for a sequential implementation of Horner’s scheme in the case of polynomials with real coefficients. From this figure it follows that the structure of this profile is very simple and consists of two linear (or sequential) searches of elements performed for two real arrays in parallel.
However, this simple example shows that, in order to completely understand a general structure of memory access, it is necessary to carefully analyze this structure at the level of individual memory references. Figure 3 illustrates fragment 1 highlighted in green in Fig.2. As can be seen, the upper sequential search is somewhat different from the lower one: in the first case, each element is referenced twice in succession. Note, however, this refinement of the memory-access profile structure has a little effect on the locality of the entire profile.
On the whole, the general memory-access profile possesses a high spatial locality, since the search of elements in the arrays is performed sequentially. However, the temporal locality is very low, since each element of one of the arrays is referenced only twice, whereas the elements of the second array are not reused at all.
2.2.1.2 Quantitative estimation of locality
The main fragment of the implementation used to obtain the quantitative estimates is given here (the KernelHorner function). The start conditions are discussed in here.
The first estimate is made on the basis of the daps characteristic used to evaluate the number of write and read operations per second. This characteristic is similar to the flops estimate for memory access and is an estimate of the memory usage performance rather than an estimate of locality. However, the daps characteristic is a good information source and can be used to compare with the results obtained according to the cvg characteristic.
Figure 4 illustrates the daps values for a number of some widespread algorithms. These values are given in increasing order: a higher performance corresponds to a larger daps value. From this figure it follows that the implementation of Horner’s scheme is characterized by a low memory usage performance. It may appear strange that in this case the daps value is significantly less than for the STREAM tests, although the memory-access profiles are similar: several simultaneous sequential searches for the elements of arrays.
Such a behavior of the implementation under study is caused by the peculiarities of the memory structure. As mentioned above, the elements of one of the arrays are referenced twice in succession. In the source code of the implementation, however, the second reference is performed at the next iteration to the previous element:
for (int i = 1; i < size; i++) {
c[i] = a[i] + c[i - 1] * x;
}
Hence, we have the case when the iterations are dependent. As a result, the hardware prefetcher badly prefetches the required cache rows, which leads to a significant slowing of the program speed compared to the other implementations based on the sequential search (for example, the STREAM tests).
Our discussion shows once more that the memory structure is very complex: a minor change made in the loop body leads to an expectedly serious slowing of the program.
The cvg characteristic is used to obtain a more machine-independent estimate of locality and to specify the frequency of fetching data to the cache memory. A lesser cvg value corresponds to a higher level of locality and to a smaller number of using the fetching procedure.
Figure 5 shows the cvg values for the same implementations presented in Fig. 4. These values are given in decreasing order: a higher locality level corresponds to a smaller cvg value. From this figure it follows that the implementation of Horner’s scheme possesses a very high locality according to the cvg estimate.
As shown above, this conclusion does not correspond to the actual memory-access performance because of the peculiarities of the memory structure. However, it is necessary to state the following two remarks. First, the cases when the memory-access performance strongly depends on the hardware peculiarities of the memory structure are not very often in practice. Second, the cvg characteristic is used to obtain a machine-independent estimate of locality; hence, it is not possible to take into account such hardware peculiarities when the analysis of memory access is performed in the framework of complete machine independence.
2.3 Approaches and features of implementing Horner’s algorithm in parallel
This algorithm is not designed to be implemented in parallel.
2.4 Scalability of Horner’s algorithm and its implementation
Scalability is not analyzed, since Horner’s algorithm is not designed to be implemented in parallel.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Existing implementations of Horner’s algorithm
In addition to the above simplest implementation, there exist more primitive codes implementing only a part of Horner’s scheme. This can be explained by the fact that in many cases it is necessary to know the value of a polynomial (the remainder of division), but it is not necessary to know only the quotient polynomial with the remainder dropped. In such cases one and the same scalar should be used instead of all the elements of the array b.