Difference between revisions of "Horners method"
| [unchecked revision] | [unchecked revision] |
(Created page with "Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (#Описание л...") |
|||
| Line 1: | Line 1: | ||
Основные авторы описания: [[Участник:Frolov|А.В.Фролов]], [[Участник:VadimVV|Вад.В.Воеводин]] ([[#Описание локальности данных и вычислений|раздел 2.2]]) | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]], [[Участник:VadimVV|Вад.В.Воеводин]] ([[#Описание локальности данных и вычислений|раздел 2.2]]) | ||
| − | == | + | == Properties and structure of Horner’s scheme == |
| − | === | + | === Description of the algorithm === |
| − | ==== | + | ==== Formulation of the problem ==== |
| − | + | Horner’s scheme is devoted to the division of a polynomial <math>P_n(x)</math> with known coefficients by the binomial <math>x - \alpha</math>. The results of this operation are the coefficients of the polynomial <math>Q_{n - 1}(x)</math> obtained by the relation | |
| − | :<math>P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)</math> | + | :<math>P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)</math> |
| − | + | and the value <math>P_n(\alpha)</math> of the polynomial <math>P_n(x)</math> at a given point <math>\alpha</math>. | |
| − | + | Unfortunately, Horner’s method is often reduced only to the calculation of a polynomial <math>P_n(x)</math> at the point <math>\alpha</math>. | |
| − | ==== | + | ==== General scheme ==== |
| − | + | Actually, Horner’s scheme implements the long division of a polynomial by the binomial <math>x - \alpha</math>. By the Bezout theorem, the remainder of this operation is equal to the value of a polynomial <math>P_n(x)</math> at a point <math>\alpha</math>. | |
| − | === | + | === Mathematical description === |
| − | + | Input data: a one-dimensional array consisting of <math>n + 1</math> numbers <math>a_k</math> and a scalar <math>\alpha</math>. | |
| − | + | Output data: a one-dimensional array consisting of <math>n + 1</math> numbers <math>b_k</math>. | |
| − | + | The formulas of Horner's method are based on the relation | |
| − | :<math>P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)</math> | + | :<math>P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)</math>. |
| − | + | Now we represent the above polynomials in canonical form: | |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
P_n(x) & = a_0 x^n+ a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n, \\ | P_n(x) & = a_0 x^n+ a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n, \\ | ||
| − | Q_{n - 1}(x) & = b_0 x^{n - 1} + b_1 x^{n - 2} + \dots + b_{n - 2} x + b_{n - 1} | + | Q_{n - 1}(x) & = b_0 x^{n - 1} + b_1 x^{n - 2} + \dots + b_{n - 2} x + b_{n - 1}. |
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | + | By <math>b_n</math> er denote <math>P_n(\alpha)</math>. Substituting these polynomials in their canonical form into the above relation and equating the coefficients at equal powers of <math>x</math>, we come to the following formulas of Horner’s scheme: | |
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
b_0 & = a_0, \\ | b_0 & = a_0, \\ | ||
| − | b_k & = a_k + \alpha b_{k - 1}, \quad k = 1, \dots, n | + | b_k & = a_k + \alpha b_{k - 1}, \quad k = 1, \dots, n. |
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | + | === The computational kernel of Horner’s algorithm === | |
| − | + | The computational kernel of Horner’s algorithm in its sequential version can be represented as a sequential set of <math>n</math> «double» operations: the multiplication of elements of the output array by one and the same scalar and the addition of the result to the next element of the input array. | |
| − | + | === Macrostructure of the algorithm === | |
| − | + | From the computational kernel of Horner’s algorithm it follows that its major part consists of the sequential set of the above «double» operations. | |
| − | + | === Implementation of the sequential algorithm === | |
| − | + | The formulas of the algorithm are described above. The operations are performed in increasing order of <math>k</math>. | |
| − | + | === Sequential complexity of the algorithm === | |
| − | + | For a polynomial of degree <math>n</math>, the number of multiplications is equal to <math>n</math> and the number of additions is also equal to <math>n</math>. Hence, Horner’s algorithm is of linear complexity with respect to the number of sequential operations. | |
| − | + | === Information graph === | |
| − | = | + | The graph of the algorithm is illustrated in Fig. 1 for <math>n = 9</math>. As can be seen, the graph is sequential. |
| − | + | [[file:Basic sequental algorithm graph.png|center|thumb|800px|Fig. 1. Horner’s scheme: a sequential version.]] | |
| − | + | Here the abbreviations In (Input) and Out (Output) are used to denote the first coefficient of the input array and the value of the polynomial at a given point <math>\alpha</math>, respectively. By Op we denote the "double" operation: the multiplication of an input variable by a scalar and the addition of the result to another variable. | |
| − | === | + | === A parallelization resource of the algorithm === |
| − | + | The sequential version of Horner’s algorithm has no parallelization resource. Its parallel form consists of a single layer and is coincident with the sequential algorithm. Thus, the height of the parallel form is equal to <math>n</math> multiplications plus <math>n</math> additions. Hence, this algorithm is of linear complexity with respect to the height of the parallel form. The width of the parallel form is equal to <math>1</math>; hence, this algorithm is of constant complexity with respect to the width of the parallel form. | |
| − | === | + | === Input and output data of the algorithm === |
| − | + | Input data: an array <math>a</math> (its elements are denoted by <math>a_i</math>, where <math>i = 0, \dots, n</math>) and a scalar <math>\alpha</math>. | |
| − | + | Additional constraints: absent. | |
| − | + | Amount of input data: <nowiki/><math>n + 2</math>. | |
| − | + | Output data: an array <math>b</math> (its elements are denoted by <math>b_k</math>, where <math>k = 0, \dots, n</math>) | |
| − | + | Amount of output data:: <nowiki/><math>n + 1</math>. | |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| − | + | In the case of unlimited computer resources, the ratio of the sequential complexity to the parallel complexity is ''constant'' (1). Computational power of the algorithm considered as the ratio of the number of operations to the total amount of input and output data is equal to 1 (the number of input and output data is even larger by 1 than the number of operations). The algorithm is completely deterministic. The arcs of the information graph are local. The stability of Horner’s scheme is optimal for the calculation of the values of a polynomial with known coefficient. | |
== Программная реализация == | == Программная реализация == | ||
Revision as of 15:36, 24 May 2015
Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2)
Contents
- 1 Properties and structure of Horner’s scheme
- 1.1 Description of the algorithm
- 1.2 Mathematical description
- 1.3 The computational kernel of Horner’s algorithm
- 1.4 Macrostructure of the algorithm
- 1.5 Implementation of the sequential algorithm
- 1.6 Sequential complexity of the algorithm
- 1.7 Information graph
- 1.8 A parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Свойства алгоритма
- 2 Программная реализация
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Описание локальности данных и вычислений
- 2.3 Возможные способы и особенности реализации параллельного алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
1 Properties and structure of Horner’s scheme
1.1 Description of the algorithm
1.1.1 Formulation of the problem
Horner’s scheme is devoted to the division of a polynomial [math]P_n(x)[/math] with known coefficients by the binomial [math]x - \alpha[/math]. The results of this operation are the coefficients of the polynomial [math]Q_{n - 1}(x)[/math] obtained by the relation
- [math]P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)[/math]
and the value [math]P_n(\alpha)[/math] of the polynomial [math]P_n(x)[/math] at a given point [math]\alpha[/math].
Unfortunately, Horner’s method is often reduced only to the calculation of a polynomial [math]P_n(x)[/math] at the point [math]\alpha[/math].
1.1.2 General scheme
Actually, Horner’s scheme implements the long division of a polynomial by the binomial [math]x - \alpha[/math]. By the Bezout theorem, the remainder of this operation is equal to the value of a polynomial [math]P_n(x)[/math] at a point [math]\alpha[/math].
1.2 Mathematical description
Input data: a one-dimensional array consisting of [math]n + 1[/math] numbers [math]a_k[/math] and a scalar [math]\alpha[/math].
Output data: a one-dimensional array consisting of [math]n + 1[/math] numbers [math]b_k[/math].
The formulas of Horner's method are based on the relation
- [math]P_n(x) - P_n(\alpha) = (x - \alpha) Q_{n - 1}(x)[/math].
Now we represent the above polynomials in canonical form:
- [math] \begin{align} P_n(x) & = a_0 x^n+ a_1 x^{n - 1} + \dots + a_{n - 1} x + a_n, \\ Q_{n - 1}(x) & = b_0 x^{n - 1} + b_1 x^{n - 2} + \dots + b_{n - 2} x + b_{n - 1}. \end{align} [/math]
By [math]b_n[/math] er denote [math]P_n(\alpha)[/math]. Substituting these polynomials in their canonical form into the above relation and equating the coefficients at equal powers of [math]x[/math], we come to the following formulas of Horner’s scheme:
- [math] \begin{align} b_0 & = a_0, \\ b_k & = a_k + \alpha b_{k - 1}, \quad k = 1, \dots, n. \end{align} [/math]
1.3 The computational kernel of Horner’s algorithm
The computational kernel of Horner’s algorithm in its sequential version can be represented as a sequential set of [math]n[/math] «double» operations: the multiplication of elements of the output array by one and the same scalar and the addition of the result to the next element of the input array.
1.4 Macrostructure of the algorithm
From the computational kernel of Horner’s algorithm it follows that its major part consists of the sequential set of the above «double» operations.
1.5 Implementation of the sequential algorithm
The formulas of the algorithm are described above. The operations are performed in increasing order of [math]k[/math].
1.6 Sequential complexity of the algorithm
For a polynomial of degree [math]n[/math], the number of multiplications is equal to [math]n[/math] and the number of additions is also equal to [math]n[/math]. Hence, Horner’s algorithm is of linear complexity with respect to the number of sequential operations.
1.7 Information graph
The graph of the algorithm is illustrated in Fig. 1 for [math]n = 9[/math]. As can be seen, the graph is sequential.
Here the abbreviations In (Input) and Out (Output) are used to denote the first coefficient of the input array and the value of the polynomial at a given point [math]\alpha[/math], respectively. By Op we denote the "double" operation: the multiplication of an input variable by a scalar and the addition of the result to another variable.
1.8 A parallelization resource of the algorithm
The sequential version of Horner’s algorithm has no parallelization resource. Its parallel form consists of a single layer and is coincident with the sequential algorithm. Thus, the height of the parallel form is equal to [math]n[/math] multiplications plus [math]n[/math] additions. Hence, this algorithm is of linear complexity with respect to the height of the parallel form. The width of the parallel form is equal to [math]1[/math]; hence, this algorithm is of constant complexity with respect to the width of the parallel form.
1.9 Input and output data of the algorithm
Input data: an array [math]a[/math] (its elements are denoted by [math]a_i[/math], where [math]i = 0, \dots, n[/math]) and a scalar [math]\alpha[/math].
Additional constraints: absent.
Amount of input data: [math]n + 2[/math].
Output data: an array [math]b[/math] (its elements are denoted by [math]b_k[/math], where [math]k = 0, \dots, n[/math])
Amount of output data:: [math]n + 1[/math].
1.10 Свойства алгоритма
In the case of unlimited computer resources, the ratio of the sequential complexity to the parallel complexity is constant (1). Computational power of the algorithm considered as the ratio of the number of operations to the total amount of input and output data is equal to 1 (the number of input and output data is even larger by 1 than the number of operations). The algorithm is completely deterministic. The arcs of the information graph are local. The stability of Horner’s scheme is optimal for the calculation of the values of a polynomial with known coefficient.
2 Программная реализация
2.1 Особенности реализации последовательного алгоритма
На Фортране схему Горнера можно записать так:
b(0) = a(0)
DO I = 1, N
b(I) = a(I)+b(I-1)*alpha
END DO
2.2 Описание локальности данных и вычислений
2.2.1 Описание локальности реализации алгоритма
2.2.1.1 Описание структуры обращений в память и качественная оценка локальности
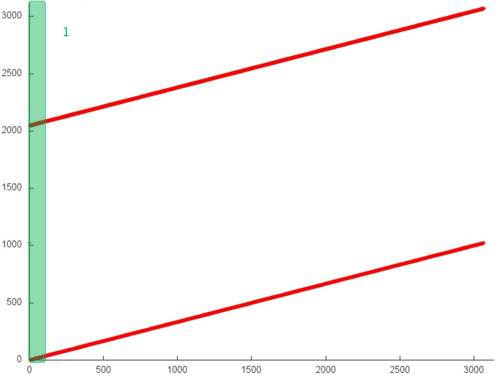
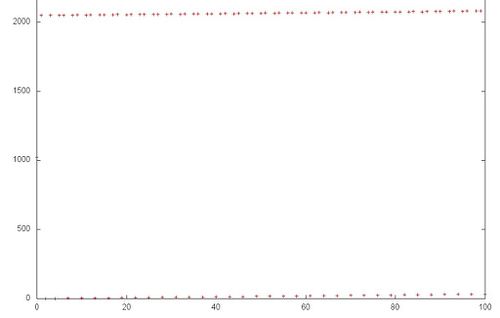
На рис. 12.1 представлен профиль обращений в память последовательной вещественной реализации схемы Горнера. Исходя из рисунка 12.1, данный профиль устроен очень просто и состоит из двух последовательных переборов элементов, выполняемых параллельно для двух массивов.
Однако даже в таком простом примере для полного понимания структуры обращений в память нужен более детальный анализ на уровне отдельных обращений. На рис. 12.2 рассмотрим подробнее фрагмент 1, выделенный на рис. 12.1 зеленым. Можно увидеть, что верхний последовательный перебор несколько отличается от нижнего – в первом случае к каждому элементу выполняется по два обращения подряд. Отметим, однако, что данное уточнение строения профиля слабо сказывается на локальности всего профиля.
В целом, общий профиль обладает высокой пространственной локальностью, поскольку перебор элементов массивов осуществляется последовательно, однако очень низкой временно́й локальностью – в одном из массивов к каждому элементу выполняется обращение только дважды, во втором массиве повторные обращения вообще отсутствуют.
2.2.1.2 Количественная оценка локальности
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция KernelGorner). Условия запуска описаны здесь.
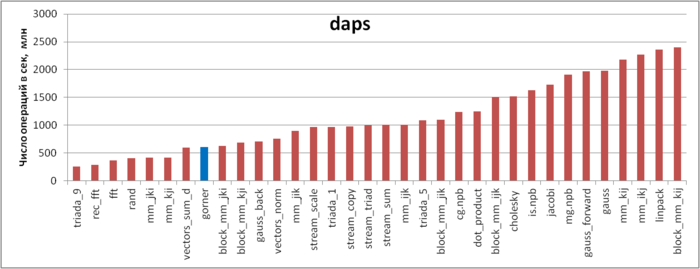
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 12.3 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Согласно данному рисунку, реализация схемы Горнера показывает низкую производительность работы с памятью. Может показаться странным, что значение daps в этом случае значительно меньше, чем для тестов STREAM, несмотря на то, что профиль обращений во всех случаях очень похож – несколько одновременно выполняемых последовательных переборов массивов.
Причина такого поведения связана с особенностями строения подсистемы памяти. В реализации схемы Горнера, как было отмечено выше, к элементам одного из массивов выполняется по два обращения подряд. Однако если посмотреть исходный код реализации, можно увидеть, что на самом деле второе обращение выполняется на следующей итерации – это обращение к предыдущему элементу:
for (int i = 1; i < size; i++) {
c[i] = a[i] + c[i - 1] * x;
}
В результате из-за зависимости итераций аппаратный префетчер гораздо хуже справляется с подтягиванием требуемых кэш-строк, что приводит к заметному замедлению выполнения программы по сравнению с другими реализациями, основанными на последовательном переборе (например, тесты STREAM).
Подобный пример лишний раз показывает, насколько сложно утроена подсистема памяти – совсем небольшое изменение строения тела цикла приводит к достаточно неожиданному серьезному замедлению программы.
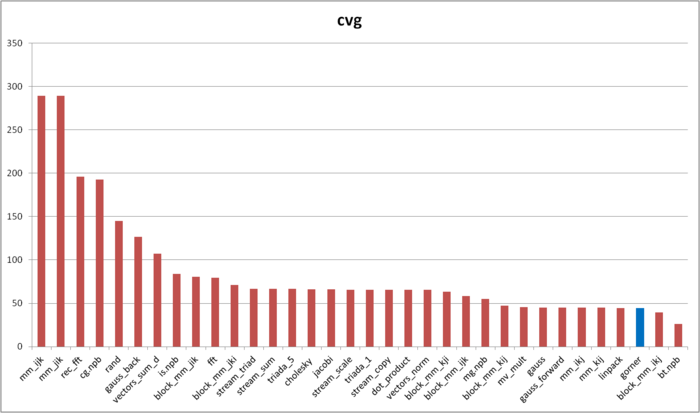
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рисунке 12.4 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что реализация схема Горнера обладает очень высокой локальностью согласно оценке cvg.
Как мы видели ранее, это плохо соотносится с реальной производительностью работы с памятью из-за особенностей строения памяти. Однако здесь необходимо сделать два замечания. Во-первых, подобные случаи, когда производительность работы с памятью настолько сильно зависит от специфичных аппаратных особенностей строения подсистемы памяти, на практике встречаются не так часто. Во-вторых, cvg предназначена для получения машинно-независимой оценки локальности; на данном уровне учесть подобные аппаратные особенности, по крайней мере, без потери доли машинно-независимых свойств, вряд ли представляется возможным.
2.3 Возможные способы и особенности реализации параллельного алгоритма
Описываемый алгоритм не предполагает параллельной реализации.
2.4 Масштабируемость алгоритма и его реализации
Понятие масштабируемости неприменимо, поскольку описываемый алгоритм не предполагает параллельной реализации.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Помимо выписанной выше простейшей реализации, существуют более примитивные коды, реализующие часть функционала схемы Горнера. Это объясняется тем, что для многих нужно только значение многочлена (остаток от деления), но не нужен многочлен-частное. В таком случае вместо всех элементов массива [math]b[/math] используется один и тот же скаляр.