Difference between revisions of "Householder (reflections) method for reducing a symmetric matrix to tridiagonal form"
| [unchecked revision] | [unchecked revision] |
| Line 38: | Line 38: | ||
=== Computational kernel of the algorithm === | === Computational kernel of the algorithm === | ||
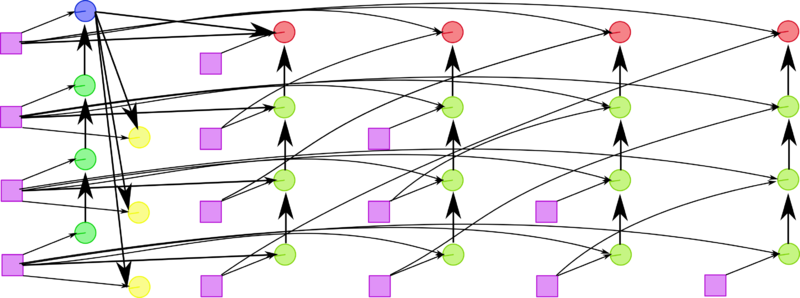
| − | [[File:HausLeftSym1.png|thumb|right|800px|Figure 1. Graph of the first half of one step in the reduction to tri-diagonal form. The input data are shown. The figure corresponds to step <math>n-4</math>. Squares denote the results obtained at the preceding step. At the first step, squares denote the input data. Green circles are used for operations of the type <math>a+b^2</math>, while lime green circles are used for operations of the type <math>a+bc</math>. | + | [[File:HausLeftSym1.png|thumb|right|800px|Figure 1. Graph of the first half of one step in the reduction to tri-diagonal form. The input data are shown. The figure corresponds to step <math>n-4</math>. Squares denote the results obtained at the preceding step. At the first step, squares denote the input data. Green circles are used for operations of the type <math>a+b^2</math>, while lime green circles are used for operations of the type <math>a+bc</math>. The blue circle denotes the calculation of reflection parameters. Light red circles correspond to the calculation of the coefficients <math>\beta_i</math> for the next half-step, while yellow circles correspond to the calculation of the vector <math>v</math>.]] |
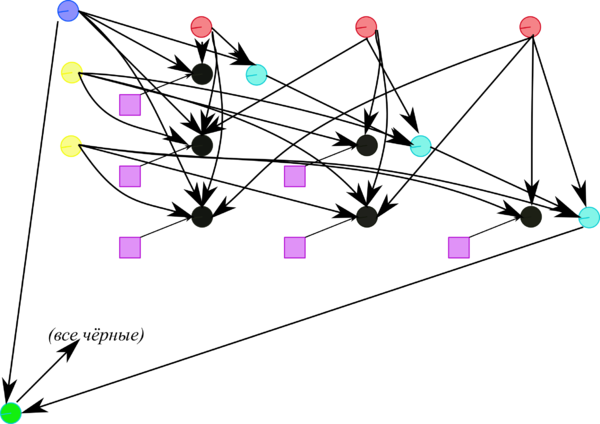
[[File:HousLeftSym2.png|thumb|right|600px|Рисунок 2. Граф второй половины шага алгоритма приведения к трёхдиагональному виду с отображением входных данных. Изображён граф первой половины шага с номером <math>n-3</math>. Квадраты - результаты выполнения предыдущего шага. Если шаг первый, то это входные данные. Синий, жёлтые и светло-красные кружки выполняются на первом полушаге (см. Рисунок 1). Голубые кружки - операции <math>a+bc</math>, зелёное - умножение, чёрные - операции <math>a+bc+de+fce</math>.]] | [[File:HousLeftSym2.png|thumb|right|600px|Рисунок 2. Граф второй половины шага алгоритма приведения к трёхдиагональному виду с отображением входных данных. Изображён граф первой половины шага с номером <math>n-3</math>. Квадраты - результаты выполнения предыдущего шага. Если шаг первый, то это входные данные. Синий, жёлтые и светло-красные кружки выполняются на первом полушаге (см. Рисунок 1). Голубые кружки - операции <math>a+bc</math>, зелёное - умножение, чёрные - операции <math>a+bc+de+fce</math>.]] | ||
Revision as of 11:57, 2 November 2017
| Приведение симметричной вещественной матрицы к трёхдиагональному виду методом Хаусхолдера (отражений) | |
| Sequential algorithm | |
| Serial complexity | [math]O(n^3)[/math] |
| Input data | [math](n^2+n)/2[/math] |
| Output data | [math](n^2+3n)/2[/math] |
| Parallel algorithm | |
| Parallel form height | [math]2n^2+O(n)[/math] |
| Parallel form width | [math]n^2/2[/math] |
Primary authors of this description: A.V.Frolov
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The Householder method (which, in Russian mathematical literature, is more often called the reflection method) is used for bringing real symmetric matrices to tri-diagonal form or, which is the same, for obtaining the decomposition [math]A=QTQ^T[/math] (where [math]Q[/math] is an orthogonal matrix and [math]T[/math] is a symmetric tri-diagonal matrix)[1]. The matrix [math]Q[/math] is stored and used not as a full square array but as the product of reflection matrices [2]. Each of these reflections is determined by a vector. For the classical implementation of the reflection method, this makes it possible to store the results of decomposition in place of the matrix A plus additional one-dimensional array.
It is the classical implementation that is discussed here. Techniques like the doubling method for calculating dot products are not used.
1.2 Mathematical description of the algorithm
The Householder method for calculating the [math]QTQ^T[/math] decomposition multiplies the current matrix by a Householder (reflection) matrix on the left and then on the right.
The [math]i[/math]-th step of the method eliminates the nonzero off-diagonal entries in the [math]i[/math]-th column beginning from the [math]i+2[/math]-th entry. For this, the left multiplication by a reflection is used. The right multiplication by the same reflection automatically eliminates the nonzero off-diagonal entries in the [math]i[/math]-th row beginning from the [math]i+2[/math]-th entry; moreover, the resulting matrix recaptures symmetry.
At each step, the reflection is not stored as a conventional square array; instead, it is represented in the form [math]U=E-\frac{1}{\gamma}vv^*[/math], where the vector [math]v[/math] is found from the entries of the current [math]i[/math]-th column as follows:
Let [math]s[/math] be the vector of dimension [math]n+1-i[/math] formed of the entries of the [math]i[/math]-th column beginning from the [math]i[/math]-th entry.
If [math](s,s)=0[/math], then [math]v=e_{i}[/math] and [math]\gamma = \frac{1}{2}[/math].
Otherwise, calculate [math]u = \frac{1}{\sqrt{(s,s)}}s[/math]. Then set [math]v_{j}=0[/math] for [math]j \lt i[/math], [math]v_{j}=u_{j-i+1}[/math] for [math]j \gt i[/math], and [math]v_{i}=1[/math] if [math]u_{1}=0[/math] and [math]v_{i}=\frac{u_{1}}{|u_{1}|}(1+|u_{1}|)[/math], otherwise. Moreover, [math]\gamma = 1+|u_{1}|=|v_{i}|[/math].
After calculating the vector [math]v[/math], one modifies sub-columns located to the right of the pivot column using the formulas [math]x'=x-\frac{(x,v)}{\gamma}v[/math]. Then the rows below the pivot row are modified via similar formulas. Using the already calculated vector [math]v[/math] and the associativity of operations, one can write out modification formulas for all the entries located to the right of and below the pivot column and row. Suppose that, for each column [math]x^{(j)}[/math] indexed by [math]j[/math], we know the number [math]\beta_{j}=\frac{(x^{(j)},v)}{\gamma}[/math]. Then the entry of the matrix [math]y[/math] in position [math](i,j)[/math] is modified according the formula [math]y' = y - \beta_{i} v_{i} - \beta_{j} v_{j} - \Delta v_{i} v_{j}[/math], where [math]\Delta = \frac{(\beta,v)}{\gamma}[/math]. At every step of the algorithm, such modifications for different pairs [math](i,j)[/math] may be performed independently; in particular, they can be carried out in parallel.
1.3 Computational kernel of the algorithm
Основную часть алгоритма составляют вычисления на каждом шагу скалярных произведений [math](s,s)[/math] и [math](x,v)[/math] для всех подстолбцов [math]x[/math]справа от текущего, а также проводимые над нижним правым квадратом матрицы операции вида [math]y'=y-ab-cd-fbd[/math], с учётом симметрии матрицы.
1.4 Macro structure of the algorithm
Как уже сказано в описании ядра, основная часть - вычисления на каждом шагу скалярных произведений [math](s,s)[/math] и [math](x,v)[/math] для всех подстолбцов [math]x[/math] справа от текущего, а также массовые покомпонентные операции [math]y'=y-ab-cd-fbd[/math]. При этом, однако, строгая последовательность выполнения первых двух подшагов не обязательна, в силу связи получаемых векторов [math]s[/math] и [math]v[/math] можно одновременно с [math](s,s)[/math] вычислять и произведения [math](x,s)[/math] с последующим выражением через них коэффициентов модификации. Это позволяет почти вдвое уменьшать критический путь графа алгоритма.
1.5 Implementation scheme of the serial algorithm
Последовательность выполнения алгоритма обычно записывается как последовательное "обнуление" поддиагональных элементов столбцов, начиная с 1-го столбца и заканчивая предпоследним [math](n-1)[/math]-м.
При этом в каждом "обнуляемом" [math]i[/math]-м столбце "обнуляются" сразу все его поддиагональные элементы одновременно, с [math](i+1)[/math]-го до [math]n[/math]-го.
Каждое "обнуление" [math]i[/math]-го столбца состоит из двух шагов: а) вычисление параметров матрицы отражения [math]U_{i}[/math] такой, чтобы при умножении на неё слева "обнулились" все поддиагональные его элементы; б) одновременное умножение слева матрицы отражения [math]U_{i}[/math] и справа матрицы отражения [math]U_{i}^T[/math]на текущую версию матрицы.
1.6 Serial complexity of the algorithm
В последовательной версии основная сложность алгоритма определяется прежде всего вычислениями скалярных произведений векторов, а также массовых модификаций элементов вида [math]y'=y-\alpha v - \beta w - \Delta vw[/math]. Они, если не учитывать возможную разреженность, составляют (в главном члене) по [math]O(n^3)[/math] операций действительного умножения и сложения/вычитания.
При классификации по последовательной сложности, таким образом, метод Хаусхолдера относится к алгоритмам с кубической сложностью.
1.7 Information graph
На рисунках 1 и 2 приведён граф алгоритма шага метода Хаусхолдера в наиболее его быстром (с параллельной точки зрения) варианте, использующем то, что с точностью до множителя ведущий вектор матрицы отражения отличается отличается от подстолбца, где выполняется очередное исключение, только одним элементом.
1.8 Parallelization resource of the algorithm
Для понимания ресурса параллелизма в симметричном приведении матрицы порядка [math]n[/math] к трёхдиагональной методом Хаусхолдера нужно рассмотреть критический путь графа.
Как видно из описания разных вершин, вычисления при "обнулении" [math]i[/math]-го столбца параметров отражения и скалярных произведений состоят из основной части - ветви длиной по [math]2(n-i)[/math] умножений и сложений - и коррекции вычислений, которые составляют [math]O(1)[/math] операций.
Поэтому по грубой (без членов низших порядков) оценке критический путь метода Хаусхолдера будет идти через [math]n^2[/math] умножений и [math]n^2[/math] сложений/вычитаний.
Поэтому в параллельном варианте, как и в последовательном, основную долю требуемого для выполнения алгоритма времени будут определять операции вида [math]a+bc[/math].
При классификации по высоте ЯПФ, таким образом, метод Хаусхолдера относится к алгоритмам с квадратичной сложностью. При классификации по ширине ЯПФ его сложность будет также квадратичной (без расширения ряда ярусов, связанных с векторными операциями сложения, пришлось бы увеличить вдвое длину критического пути).
1.9 Input and output data of the algorithm
Входные данные: плотная симметричная квадратная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Объём входных данных: [math](n^2+n)/2[/math].
Выходные данные: трёхдиагональная матрица [math]D[/math] (ненулевые элементы [math]r_{ij}[/math] в последовательном варианте хранятся в элементах исходной матрицы [math]a_{ij}[/math]), унитарная (ортогональная) матрица Q - как произведение матриц Хаусхолдера (отражения) (их вектора нормалей к плоскостям отражения в последовательном варианте хранятся в поддиагональных элементах исходной матрицы [math]a_{ij}[/math] и в одном дополнительном столбце размерности n).
Объём выходных данных: [math](n^2+3n)/2[/math].
1.10 Properties of the algorithm
Соотношение последовательной и параллельной сложности, как хорошо видно, является линейным, что даёт определённый стимул для распараллеливания. Однако у наискорейшей ЯПФ ширина квадратична, что указывает на дисбаланс между загруженностями устройств при попытке её реально запрограммировать. Поэтому более практично даже при хорошей (быстрой) вычислительной сети оставить количество устройств (например, узлов кластера) линейным по размеру матрицы, что удвоит критический путь реализуемой ЯПФ.
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна.
Алгоритм в рамках выбранной версии полностью детерминирован.
Вычислительная погрешность в методе отражений (Хаусхолдера) растет линейно, как и в методе Гивенса (вращений).
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
В варианте с кратчайшим критическим путём графа алгоритма (с использованием зависимости между обнуляемым вектором и направляющим вектором отражения) метод Хаусхолдера (отражений) приведения квадратной симметричной вещественной матрицы к трёхдиагональному виду на Фортране 77 можно записать так:
DO I = 1, N-2
DO K = I, N
SX(K)=A(N,I)*A(N,K)
END DO
DO J = N-1, I+1, -1
SX(I)=SX(I)+A(J,I)*A(J,I)
END DO
DO K = I+1, N
DO J = N-1, K, -1
SX(K)=SX(K)+A(J,I)*A(J,K)
END DO
DO J = K-1,I+1,-1
SX(K)=SX(K)+A(J,I)*A(K,J)
END DO
END DO
ALPHA = SQRT (SX(I))
IF (A(I+1,I).NE.0.) THEN
BETA = 1./ALPHA
DO J = I+2, N
A(J,I)=A(J,I)*BETA
END DO
SX(I) = A(I+1,I)*BETA+SIGN(1.,A(I+1,I))
A(I+1,I)=ALPHA
G=1./ABS(SX(I)) ! 1/gamma
SX2=0.
DO K = I+2, N
SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
SX2=SX(K)*A(K,I)+SX2
END DO
SX2=G*SX2
DO K = I+2, N
A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
DO J = K+1, N
A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
END DO
END DO
ELSE
IF (ALPHA.NE.0.) THEN
BETA = 1./ALPHA
DO J = I+2, N
A(J,I)=A(J,I)*BETA
END DO
SX(I) = -1.
A(I+1,I)=ALPHA
G=1.! 1/gamma
SX2=0.
DO K = I+2, N
SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
SX2=SX(K)*A(K,I)+SX2
END DO
SX2=G*SX2
DO K = I+2, N
A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
DO J = K+1, N
A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
END DO
END DO
ELSE
SX(I)=1.
END IF
END IF
END DO
Здесь симметричная трёхдиагональная матрица хранится в диагонали и нижней кодиагонали массива A, вектора v - в поддиагональной части массива, за исключением первых их элементов, для которых выделен массив SX.
Обычно же в последовательных версиях коэффициенты модификаций столбцов вычисляются целиком через скалярные произведения после вычислений параметров матрицы отражения. При этом схема чуть проще. Удлиняется критический путь графа, но для последовательных реализаций это неважно.
2.2 Locality of data and computations
К сожалению, в графе, как видно по рисунку, в наличии пучки рассылок, в них неизбежно часть дуг остаются длинными, что отрицательно влияет на локальность вычислений по пространству.
2.2.1 Locality of implementation
2.2.1.1 Structure of memory access and a qualitative estimation of locality
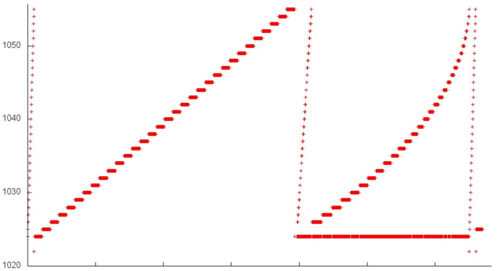
На рис. 3 представлен профиль обращений в память для реализации метода Хаусхолдера (отражений) для приведения симметричных матриц к трёхдиагональному виду. Данный профиль обладает явной итерационной структурой, при этом видно, что итерации очень похожи. Основное их отличие заключается в наборе используемых данных – на каждой следующей итерации несколько первых элементов отбрасываются их рассмотрения, то есть чем позже итерация, тем меньше данных в ней задействовано. Также можно отметить, что число обращений в каждой последующей итерации немного уменьшается. Для того чтобы проанализировать общий профиль, в таком случае чаще всего достаточно изучить одну итерацию. Рассмотрим самую первую из них более детально.
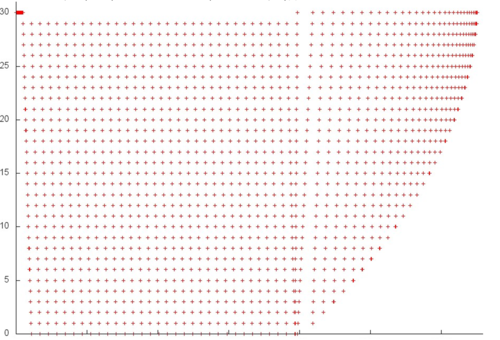
На рис. 4 показан набор обращений в рамках первой итерации (выделен на рис. 3 зеленым). Его можно разбить на несколько фрагментов и рассмотреть их отдельно. Строение фрагментов 2-5 можно оценить по общему графику для итерации. Фрагмент 2 представляет собой набор последовательных переборов в обратном порядке с небольшим шагом, причем число элементов в переборе постепенно уменьшается. Такое строение характеризуется достаточно высокой пространственной локальностью, поскольку часто происходит обращений к близко расположенным данным, однако низкой временной, поскольку данные повторно не используются. То же самое верно и для фрагмента 4, основное отличие которого заключается в том, что переборы выполняются в прямом порядке. Отметим, что некоторое искривление данного фрагмента связано не со строением самого фрагмента, а с разным числом параллельно выполняющихся обращений (см., например, правую область фрагмента 6), чего не наблюдается при выполнении фрагмента 2.
Далее, фрагменты 3 и 5 состоят из небольшого числа обращений к данным, расположенным далеко друг от друга. Такие фрагменты характеризуются низкой пространственной и временной локальностью.
Оставшиеся фрагменты требуют более детального рассмотрения. Перейдем к изучению фрагмента 1, который целиком представлен на рис. 5. Здесь мы можем видеть несколько этапов, каждый из которых представляет собой последовательный перебор элементов с шагом по памяти 1, причем в некоторых случаях данные много раз используются повторно (особенно это заметно в правой нижней области рисунка, где выполняется множество обращений к одному и тому же элементу). При условии, что в данном фрагменте задействовано всего около 40 элементов, можно говорить, что данный набор обращений обладает высокой пространственной и временной локальностью.
Далее рассмотрим детально фрагмент 6 (рис. 6). Здесь можно увидеть, что повторные обращения к данным выполняются не подряд, а через некоторые промежутки, однако число задействованных элементов также очень невелико, так что и в этом случае локальность (и пространственная, и временная) будет высокой.
В целом можно сказать, что рассматриваемая итерация обладает достаточно высокой пространственной и временной локальностью. Поскольку остальные итерации устроены подобным образом, данные вывод можно перенести и на общий профиль обращений.
2.2.1.2 Quantitative estimation of locality
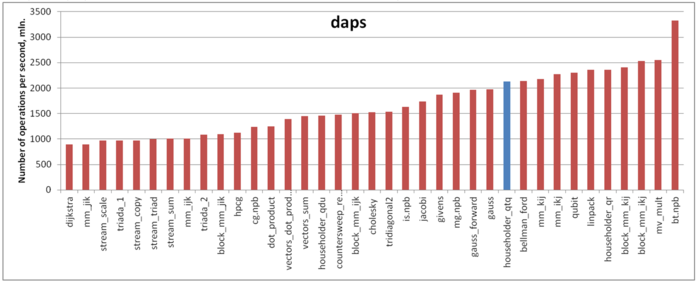
Оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 7 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность работы с памятью в данном случае достаточно высока – значение daps лишь немногим уступает тесту Linpack, который обладает высокой эффективностью работы с памятью, и немного превосходит, например, реализацию метода Якоби или метода Гаусса.
2.3 Possible methods and considerations for parallel implementation of the algorithm
2.4 Scalability of the algorithm and its implementations
2.4.1 Scalability of the algorithm
2.4.2 Scalability of of the algorithm implementation
Проведём исследование масштабируемости вширь реализации согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2" Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [16:81] с шагом n^2;
- размер матрицы [1000 : 16000] с шагом 1000.
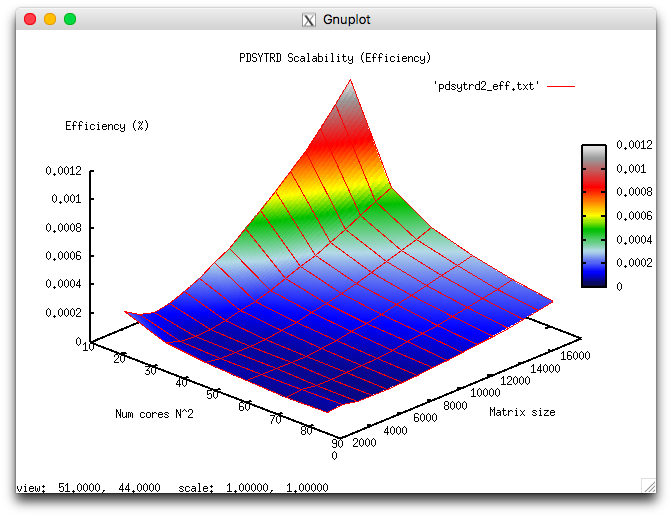
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 4.763e-05%;
- максимальная эффективность реализации 0.011%.
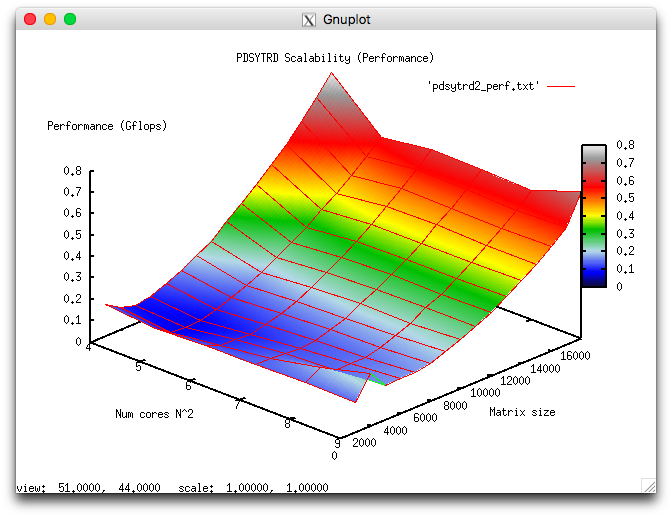
На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в процедуре PDSYTRD из Scalapack в зависимости от изменяемых параметров запуска.
2.5 Dynamic characteristics and efficiency of the algorithm implementation
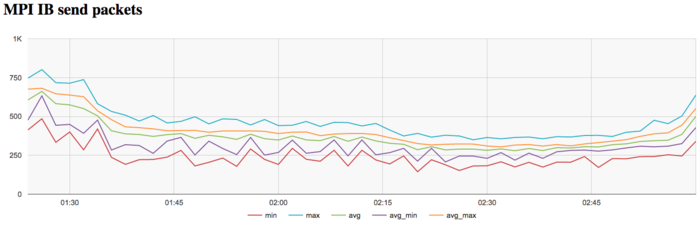
Для проведения экспериментов использовалась реализация метода Хаусхолдера, представленная в пакете SCALAPACK библиотеки Intel MKL (метод pdgehrd). Все результаты получены на суперкомпьютере «Ломоносов-2». Использовались процессоры Intel Xeon E5-2697v3, сеть FDR Infiniband а также компилятор Intel с опциями, рекомнедованными Intel MKL Advisor. На рисунках показана эффективность реализации метода Хаусхолдера (отражений) для приведения симметричных матриц к трёхдиагональному виду для размерности матрицы 15000, запуск проводился на 81 ядре.
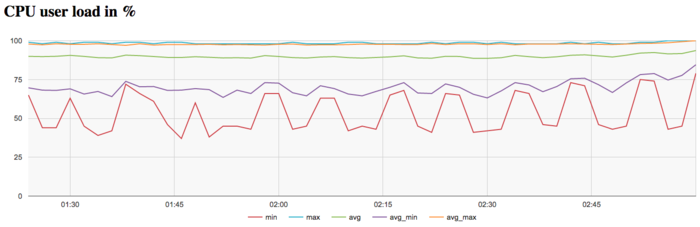
На графике загрузки процессора видно, что почти все время работы программы средний уровень загрузки составляет около 90%. Это хорошая картина для программ, запущенных c использованием технологии Hyper Threading т.е. всех виртуальных ядер доступных для данной архитектуры. К концу итерации виден более высокий уровень интенсивности вычислений в срванении со началом и серединой вычислений.
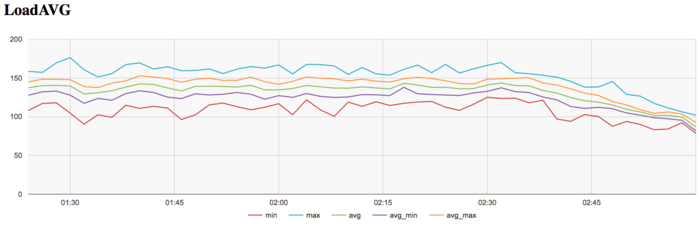
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 140 и только к концу итерации снижается до 80. Это свидетельствует о стабильной работе программы на протяжении всего выполнения со 140 нитями на одном узле или около 10 нитей на 1 физическое ядро на каждом узле. Это указывает на статичную загрузку аппаратных ресурсов процессами, однако их число для узла слишком велико, что с одной стороны может указывать на не очень рациональные опции компиляции, который могут приводить к снижению производительности из-за накладных расходов на переключение контекста между нитями.
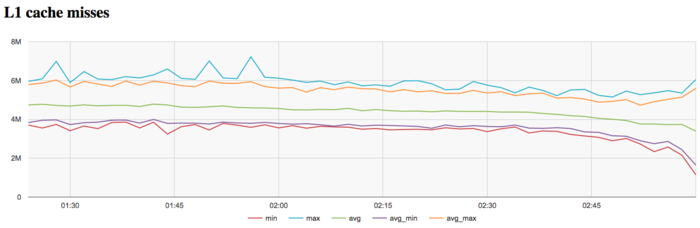
На графике кэш-промахов первого уровня видно, что число промахов достаточно низкое и находится на уровне 5 млн/сек в среднем по всем узлам. Интересен факт снижения числа промахов к концу итерации, хотя снижение и не очень значительное, но вполне заметное.
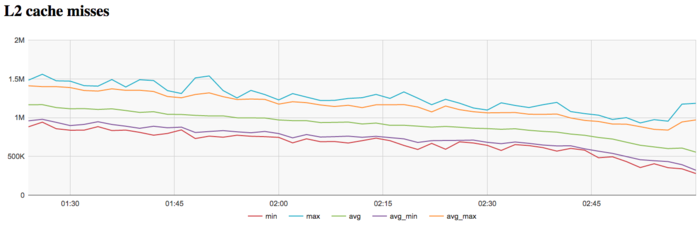
На графике кэш-промахов второго уровня видно, что число промахов достаточно тоже низкое и находится на уровне 1 млн/сек в среднем по всем узлам. На графике промахов второго уровня факт снижения числа промахов к концу итерации проявляется более явно и снижение и более значительное и заметное (с 1.2 млн до 0.5 млн.).
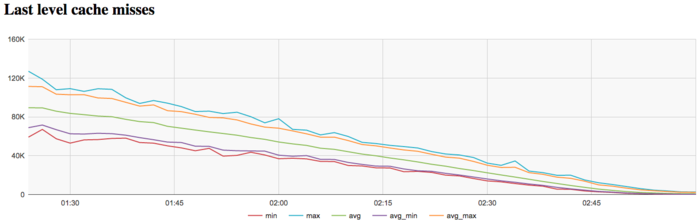
На графике кэш-промахов последнего уровня видно, что число промахов достаточно небольшое и быстро убывает с уровня 90 тыс/сек до 0 в среднем по всем узлам. Это указывает на то, что задача достаточно хорошо укладывается в кэш-память третьего уровня, особенно к концу итерации.
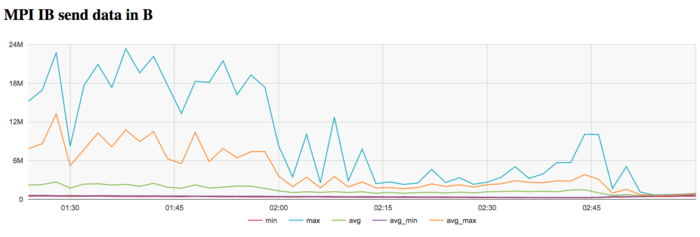
На графике скорости передачи данных по сети Infiniband наблюдается достаточно низкая интенсивность использования коммуникационной сети на каждой итерации. Причем к концу каждой итерации интенсивность передачи данных сильно снижается. Это указывает на бОльшую необходимость в обмене данными между процессами в начале итерации и большую локальность вычислений к концу итерации.
На графике скорости передачи данных в пакетах в секунду наблюдается большая «кучность» показаний максимального минимального и среднего значений в сравнении с графиком скорости передачи в байт/сек. Это говорит о том, что, вероятно, процессы обмениваются сообщениями различной длины, что указывает на неравномерное распределение данных. Также наблюдается рост интенсивности использования сети к концу каждой итерации. Особенно это различие заметно к концу итерации.
В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала стабильно и эффективно использовала память. Использование памяти и коммуникационной среды не достаточно интенсивное, что может стать указывать на факторы снижения эффективности и увеличении производительности при существенном росте размера задачи. Для существующей в SCALAPACK параллельной реализаций характерно сильное снижение числа кэш-промахов и обменов к концу итерации
2.6 Conclusions for different classes of computer architecture
В сравнении с методом Гивенса, который имеет естественное двумерное блочное разбиение на основе точечного метода, метод Хаусхолдера из-за худших характеристик локальности (наличие пучков рассылок) и меньшего количества независимых обобщённых развёрток графа не так хорош для реализаций на системах с распределённой памятью, как для систем с общей памятью. Поэтому на массово параллельных системах с распределённой памятью следует применять метод Хаусхолдера (если уж именно его нужно реализовать) не в точечной версии, а в разрабатываемых исследователями блочных вариантах. Следует отметить, что эти варианты - не блочная нарезка описанного метода, а самостоятельные методы. Особенно их применение рекомендуется в случаях с большой разрежённостью матрицы.
2.7 Existing implementations of the algorithm
Большинство пакетов от LINPACKа и LAPACKa до SCALAPACKa используют для QR-разложения матриц именно метод Хаусхолдера, правда, в различных модификациях (обычно с использованием BLAS). Существует большая подборка исследовательских работ по блочным версиям.