Householder (reflections) method for reducing a symmetric matrix to tridiagonal form

The Householder (reflection) method for reducing symmetric matrices to tridiagonal form
Sequential algorithm
Serial complexity	[math]O(n^3)[/math]
Input data	[math](n^2+n)/2[/math]
Output data	[math](n^2+3n)/2[/math]
Parallel algorithm
Parallel form height	[math]2n^2+O(n)[/math]
Parallel form width	[math]n^2/2[/math]

Primary authors of this description: A.V.Frolov

1 Properties and structure of the algorithm

1.1 General description of the algorithm

The Householder method (which, in Russian mathematical literature, is more often called the reflection method) is used for bringing real symmetric matrices to tri-diagonal form or, which is the same, for obtaining the decomposition [math]A=QTQ^T[/math] (where [math]Q[/math] is an orthogonal matrix and [math]T[/math] is a symmetric tri-diagonal matrix). The matrix [math]Q[/math] is stored and used not as a full square array but as the product of reflection matrices . Each of these reflections is determined by a vector. For the classical implementation of the reflection method, this makes it possible to store the results of decomposition in place of the matrix A plus additional one-dimensional array.

It is the classical implementation that is discussed here. Techniques like the doubling method for calculating dot products are not used.

1.2 Mathematical description of the algorithm

The Householder method for calculating the [math]QTQ^T[/math] decomposition multiplies the current matrix by a Householder (reflection) matrix on the left and then on the right.

Reflection matrix

The [math]i[/math]-th step of the method eliminates the nonzero off-diagonal entries in the [math]i[/math]-th column beginning from the [math]i+2[/math]-th entry. For this, the left multiplication by a reflection is used. The right multiplication by the same reflection automatically eliminates the nonzero off-diagonal entries in the [math]i[/math]-th row beginning from the [math]i+2[/math]-th entry; moreover, the resulting matrix recaptures symmetry.

At each step, the reflection is not stored as a conventional square array; instead, it is represented in the form [math]U=E-\frac{1}{\gamma}vv^*[/math], where the vector [math]v[/math] is found from the entries of the current [math]i[/math]-th column as follows:

Let [math]s[/math] be the vector of dimension [math]n+1-i[/math] formed of the entries of the [math]i[/math]-th column beginning from the [math]i[/math]-th entry.

If [math](s,s)=0[/math], then [math]v=e_{i}[/math] and [math]\gamma = \frac{1}{2}[/math].

Otherwise, calculate [math]u = \frac{1}{\sqrt{(s,s)}}s[/math]. Then set [math]v_{j}=0[/math] for [math]j \lt i[/math], [math]v_{j}=u_{j-i+1}[/math] for [math]j \gt i[/math], and [math]v_{i}=1[/math] if [math]u_{1}=0[/math] and [math]v_{i}=\frac{u_{1}}{|u_{1}|}(1+|u_{1}|)[/math], otherwise. Moreover, [math]\gamma = 1+|u_{1}|=|v_{i}|[/math].

After calculating the vector [math]v[/math], one modifies sub-columns located to the right of the pivot column using the formulas [math]x'=x-\frac{(x,v)}{\gamma}v[/math]. Then the rows below the pivot row are modified via similar formulas. Using the already calculated vector [math]v[/math] and the associativity of operations, one can write out modification formulas for all the entries located to the right of and below the pivot column and row. Suppose that, for each column [math]x^{(j)}[/math] indexed by [math]j[/math], we know the number [math]\beta_{j}=\frac{(x^{(j)},v)}{\gamma}[/math]. Then the entry of the matrix [math]y[/math] in position [math](i,j)[/math] is modified according the formula [math]y' = y - \beta_{i} v_{i} - \beta_{j} v_{j} - \Delta v_{i} v_{j}[/math], where [math]\Delta = \frac{(\beta,v)}{\gamma}[/math]. At every step of the algorithm, such modifications for different pairs [math](i,j)[/math] may be performed independently; in particular, they can be carried out in parallel.

1.3 Computational kernel of the algorithm

Figure 1. Graph of the first half-step in the reduction to tri-diagonal form. The input data are shown. The figure corresponds to step [math]n-4[/math]. Squares denote the results obtained at the preceding step. At the first step, squares denote the input data. Green circles are used for operations of the type [math]a+b^2[/math], while lime green circles are used for operations of the type [math]a+bc[/math]. The blue circle denotes the calculation of reflection parameters. The light red circles correspond to the calculation of the coefficients [math]\beta_i[/math] for the next half-step, while the yellow circles correspond to the calculation of the vector [math]v[/math].

Figure 2. Graph of the second half-step in the reduction to tri-diagonal form. The input data are shown. The figure corresponds to step [math]n-3[/math]. Squares denote the results obtained at the preceding step. At the first step, squares denote the input data. The blue circle and the yellow and light red circles relate to operations performed at the first half-step (see Figure 1). The light blue and black circles denote the operations [math]a+bc[/math] and [math]a+bc+de+fce[/math], respectively, while the green circle corresponds to multiplication.

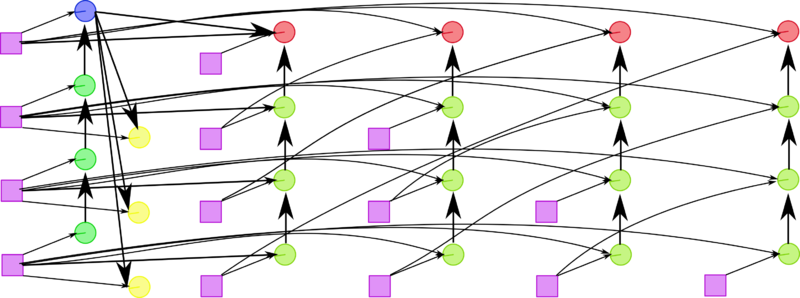
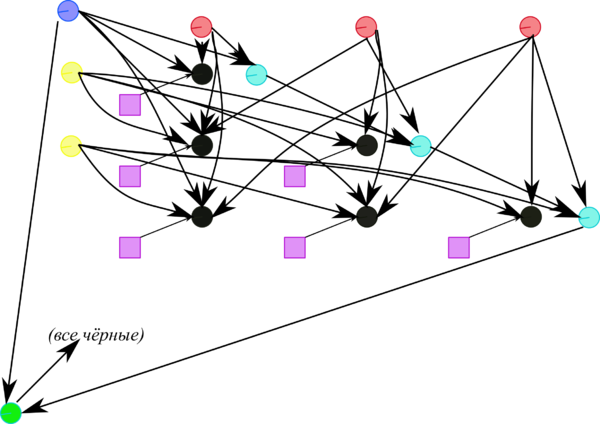
At each step of the algorithm, the bulk of calculations falls on the dot products [math](s,s)[/math] and [math](x,v)[/math] performed for all sub-columns [math]x[/math] located to the right of the pivot column, as well as on operations of the type [math]y'=y-ab-cd-fbd[/math] performed for the lower right sub-matrix with its symmetry taken into account .

1.4 Macro structure of the algorithm

As already said in the description of the computational kernel, the bulk of calculations falls on the dot products [math](s,s)[/math] and [math](x,v)[/math] performed for all sub-columns [math]x[/math] located to the right of the pivot column, as well as on the mass component-wise operations of the type [math]y'=y-ab-cd-fbd[/math]. However, the strict order in performing the first two half-steps is not mandatory. The relationship between the vectors [math]s[/math] and [math]v[/math] makes it possible to calculate the products [math](x,s)[/math] simultaneously with [math](s,s)[/math] and then to express the modification coefficients in terms of these products. This allows us to almost halve the critical path of the algorithm graph.

1.5 Implementation scheme of the serial algorithm

The traditional implementation of the algorithm is a systematic process of eliminating off-diagonal entries in the columns. This process begins from the first column and ends with the penultimate column (that is, column [math](n-1)[/math]).

If the elimination process is applied to column [math]i[/math], then all of its entries with indices from [math](i+1)[/math] to [math]n[/math] are eliminated simultaneously.

The elimination in column [math]i[/math] consists of two steps: (a) The parameters of reflection [math]U_{i}[/math] are calculated. Left multiplication by this reflection effects elimination in column [math]i[/math]. (b) The current matrix is simultaneously multiplied by the reflection [math]U_{i}[/math] on the left and on the right .

1.6 Serial complexity of the algorithm

The serial complexity of this algorithm is mainly determined by vector dot products, as well as mass modifications of the type [math]y'=y-\alpha v - \beta w - \Delta vw[/math]. If we ignore the possible sparsity of the matrix, then these operations require (in the principal term) [math]O(n^3)[/math] real multiplications and additions/subtractions.

Therefore, in terms of the number of serial operations, the Householder method should be regarded as a cubic complexity algorithm.

1.7 Information graph

Figures 1 and 2 show the graph of one step of the Householder method in its fastest version (from the viewpoint of parallel implementation). This version uses the fact that, up to a scalar factor, the vector specifying the reflection differs from the sub-column to be eliminated by only a single entry.

1.8 Parallelization resource of the algorithm

Consider the reduction of a symmetric order [math]n[/math] matrix to tri-diagonal form by the Householder method. In order to understand the parallelization resource of this method, one needs to inspect the critical path of the corresponding graph.

As is seen from the above description, the elimination in the [math]i[/math]-th column involves the calculation of the reflection parameters and certain dot products. These calculations consist of the basic part, which is a branch comprised of [math]2(n-i)[/math] multiplications and additions, and corrections that cost [math]O(1)[/math] operations.

Consequently, by a rough estimate (with terms of lower order dropped), the critical path of the Householder method goes through [math]n^2[/math] multiplications and [math]n^2[/math] additions/subtractions.

Hence, operations of the type [math]a+bc[/math] take the bulk of execution time both in the serial and parallel versions of the algorithm.

Thus, in terms of the parallel form height, the Householder method is qualified as an algorithm of quadratic complexity. In terms of the parallel form width, it also has quadratic complexity. (If the layers related to vector addition operations were not expanded, then the critical path would be doubled.)

1.9 Input and output data of the algorithm

Input data: dense square symmetric matrix [math]A[/math] (with entries [math]a_{ij}[/math]).

Size of the input data: [math](n^2+n)/2[/math].

Output data: tri-diagonal matrix [math]D[/math] (in the serial version, the nonzero entries [math]r_{ij}[/math] are stored in the positions of the original entries [math]a_{ij}[/math]), unitary (or orthogonal) matrix Q stored as the product of Householder matrices (reflections) (in the serial version, their normal vectors to reflection planes are stored in the positions of the original off-diagonal entries [math]a_{ij}[/math] and in an additional column of length n).

Size of the output data: [math](n^2+3n)/2[/math].

1.10 Properties of the algorithm

It is clearly seen that the ratio of the serial to parallel complexity is linear, which yields a certain incentive for parallelization. However, the fastest parallel form has a quadratic width. This indicates an imbalance in the workload of different units when an attempt of actual implementation is made. Even if the computational network is fine (that is, fast), it is more practical to leave the number of units (for instance, cluster nodes) linear with respect to matrix size, which doubles the critical path of the parallel form to be implemented.

The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is linear.

Within the framework of the chosen version, the algorithm is completely determined.

The roundoff errors in the Householder (reflection) method grow linearly, as they also do in the Givens (rotation) method.

2 Software implementation of the algorithm

2.1 Implementation peculiarities of the serial algorithm

Consider the Householder (reflection) method for reducing a real square symmetric matrix to tri-diagonal matrix in the version with a shortest critical path (which uses the relation between the vector under elimination and the vector that determines reflection). This method can be written in Fortran 77 as follows:

	DO  I = 1, N-2

            DO K = I, N
              SX(K)=A(N,I)*A(N,K)
            END DO
            DO J = N-1, I+1, -1
                 SX(I)=SX(I)+A(J,I)*A(J,I)
            END DO 
            DO K = I+1, N
              DO J = N-1, K, -1
                 SX(K)=SX(K)+A(J,I)*A(J,K)
              END DO
              DO J = K-1,I+1,-1
                 SX(K)=SX(K)+A(J,I)*A(K,J)
              END DO
            END DO

               ALPHA = SQRT (SX(I))
               IF (A(I+1,I).NE.0.) THEN
                  BETA = 1./ALPHA
                  DO J = I+2, N
                    A(J,I)=A(J,I)*BETA
                  END DO
                  SX(I) = A(I+1,I)*BETA+SIGN(1.,A(I+1,I))                     
                  A(I+1,I)=ALPHA
                  G=1./ABS(SX(I)) ! 1/gamma
                  SX2=0.
                  DO K = I+2, N
                     SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
                     SX2=SX(K)*A(K,I)+SX2                     
                  END DO
                  SX2=G*SX2
                  DO K = I+2, N
                     A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
                     DO J = K+1, N
                       A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
                     END DO
                  END DO
               ELSE
                  IF (ALPHA.NE.0.) THEN
                     BETA = 1./ALPHA
                     DO J = I+2, N
                       A(J,I)=A(J,I)*BETA
                     END DO
                     SX(I) = -1. 
                     A(I+1,I)=ALPHA
                     G=1.! 1/gamma
                     SX2=0.
                     DO K = I+2, N
                        SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
                        SX2=SX(K)*A(K,I)+SX2                 
                     END DO
                     SX2=G*SX2
                     DO K = I+2, N  
                        A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2                   
                        DO J = K+1, N
                          A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
                        END DO
                     END DO
                  ELSE
                     SX(I)=1.
                  END IF
               END IF               

		
	END DO

Here, the symmetric tri-diagonal matrix is stored in the locations of the principal diagonal and sub-diagonal of the array A, while the vectors v (without their first components) are stored in the off-diagonal area of this array. The first components are stored in a specially selected array SX.

Usually, in serial versions of the algorithm, the coefficients of column modifications are calculated via dot products after the parameters of reflection have already been found. This slightly simplifies the scheme of the method but extends its critical path. However, this extension is not important for serial realizations.

2.2 Possible methods and considerations for parallel implementation of the algorithm

Most of packages (from LINPACK and LAPACK to SCALAPACK) choose exactly the Householder method (in various modifications, which usually use BLAS) in order to reduce a symmetric matrix to tri-diagonal form. There is a large amount of research devoted to block versions of this method.

2.4 Conclusions for different classes of computer architecture

Compared to the Givens method, which has the natural two-dimensional partition based on the pointwise version, the Householder method is adapted for distributed memory systems worse than for shared memory ones. This is due to the fact that the locality is worse (because of the presence of packet distributions) and the number of independent generalized graph scans is smaller. Consequently, on massively parallel distributed memory systems, one should use the Householder method (if its implementation is required) in its block versions instead of the pointwise version. Note that these block versions are independent methods rather than just a block slicing of the pointwise method. The use of block versions is especially recommended when the matrix is very sparse.