Dense matrix multiplication (serial version for real matrices)
Primary authors of this description: A.V.Frolov.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Matrix multiplication is one of the basic procedures in algorithmic linear algebra, which is widely used in a number of different methods. Here, we consider the product C = AB of dense real matrices (serial real version), that is, the version in which neither a special form of matrices nor the associative properties of the addition operation are used[1].
1.2 Mathematical description of the algorithm
Input data: dense matrix A of size m-by-n (with entries a_{ij}), dense matrix B of size n-by-l (with entries b_{ij}).
Output data: dense matrix C (with entries c_{ij}).
Formulas of the method:
- \begin{align} c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad i \in [1, l]. \end{align}
There exists also a block version of the method; however, this description treats only the pointwise version.
1.3 Computational kernel of the algorithm
The computational kernel of the dense matrix multiplication can be compiled of repeated products of A with the columns of B (there are on the whole l such products) or (upon more detailed inspection) of repeated dot products of the rows of A and the columns of B (there are on the whole ml such products):
- \sum_{k = 1}^{n} a_{ik} b_{kj}
Depending on the problem requirements, these sums are calculated with or without using the accumulation mode.
1.4 Macro structure of the algorithm
As already noted in computational kernel of the algorithm description, the basic part of the dense matrix multiplication is compiled of repeated dot products of the rows of A and the columns of B (there are on the whole ml such products):
- \sum_{k = 1}^{n} a_{ik} b_{kj}
These calculations are performed with or without using the accumulation mode.
1.5 Implementation scheme of the serial algorithm
For all i from 1 to m and for all j from 1 to l, do
- c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}
We emphasize that sums of the form \sum_{k = 1}^{n} a_{ik} b_{kj} are calculated in the accumulation mode by adding the products a_{ik} b_{kj} to the current (temporary) value of c_{ij}.The index k increases from 1 to n. All the sums are initialized to zero. The general scheme is virtually the same if summations are performed in the decreasing order of indices; therefore, this case is not considered. Other orders of summation change the parallel properties of the algorithm and are considered in separate descriptions.
1.6 Serial complexity of the algorithm
The multiplication of two square matrices of order n (that is, m=n=l) in the (fastest) serial version requires
- n^3 multiplications and the same number of additions.
The multiplication of an m-by-n matrix by an n-by-l matrix in the (fastest) serial version requires
- mnl multiplications and the same number of additions.
The use of accumulation requires that multiplications and additions be done in the double precision mode (or such procedures as the Fortran function DPROD be used). This increases the computation time for performing the matrix multiplication.
In terms of serial complexity, the dense matrix multiplication is qualified as a cubic complexity algorithm (or a trilinear complexity algorithm if the matrices are rectangular).
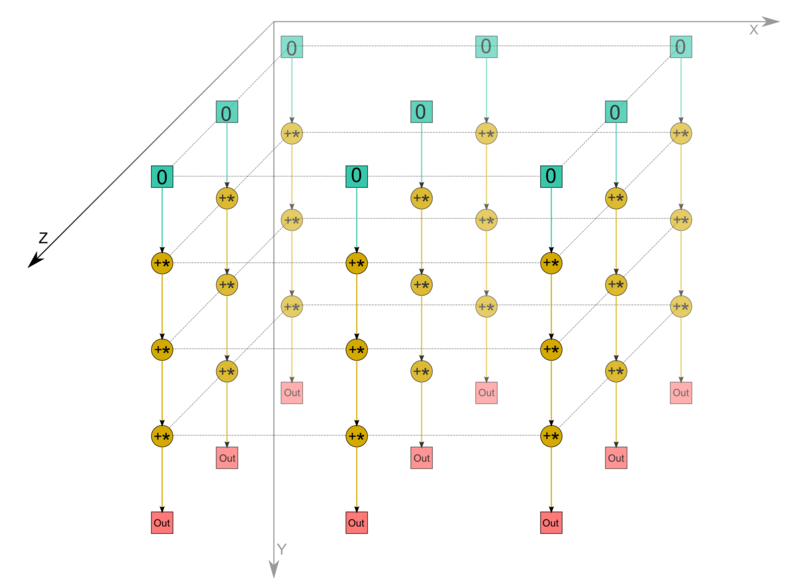
1.7 Information graph
We describe the algorithm graph both analytically and graphically.
The algorithm graph of multiplying dense matrices consists of a single group of vertices placed at integer nodes of a three-dimensional domain. The corresponding operation is a+bc.
The natural coordinates of this domain are as follows:
- i varies from 1 to m, taking all the integer values in this range;
- j varies from 1 to l, taking all the integer values in this range;
- k varies from 1 to n, taking all the integer values in this range.
The arguments of the operation are as follows:
- a is:
- the constant 0 if k = 1;
- the result of performing the operation corresponding to the vertex with coordinates i, j, k-1 if k \gt 1;
- b is the element a_{ik} of the input data;
- c is the element b_{kj} of the input data;
The result of performing the operation is:
- an intermediate data item if k \lt n;
- an output data item c_{ij} if k = n.
1.8 Parallelization resource of the algorithm
The parallel version of the algorithm for multiplying square matrices of order n requires that the following layers be successively performed:
- n layers of multiplications and the same numbers of layers for addition (there are n^2 operations in each layer).
The multiplication of an m-by-n matrix by an n-by-l matrix in the (fastest) serial version requires
- n layers of multiplications and the same numbers of layers for addition (there are ml operations in each layer).
The use of accumulation requires that multiplications and subtractions be done in the double precision mode. For the parallel version, this implies that virtually all the intermediate calculations in the algorithm must be performed in double precision if the accumulation option is used. Unlike the situation with the serial version, this results in a certain increase in the required memory size.
In terms of the parallel form height, the dense matrix multiplication is qualified as a quadratic complexity algorithm. In terms of the parallel form width, its complexity is also quadratic (for square matrices) or bilinear (for general rectangular matrices).
1.9 Input and output data of the algorithm
Input data: matrix A (with entries a_{ij}), matrix B (with entries b_{ij})).
Size of the input data : mn+nl
Output data : matrix C (with entries c_{ij}).
Size of the output data: ml
1.10 Properties of the algorithm
It is clear that, in the case of unlimited resources, the ratio of the serial to parallel complexity is quadratic or bilinear (since this is the ratio of the cubic or trilinear complexity to linear one).
The computational power of the dense matrix multiplication, understood as the ratio of the number of operations to the total size of the input and output data, is linear.
The algorithm of dense matrix multiplication is completely determined. We do not consider any other order of performing associative operations in this version.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
In its simplest form, the matrix multiplication algorithm in Fortran can be written as follows:
DO I = 1, M
DO J = 1, L
S = 0.
DO K = 1, N
S = S + DPROD(A(I,K), B(K,J))
END DO
C(I, J) = S
END DO
END DO
In this case the S variable must be double precision to implement the accumulation mode.
2.2 Possible methods and considerations for parallel implementation of the algorithm
2.3 Run results
2.4 Conclusions for different classes of computer architecture
3 References
- ↑ Voevodin V.V., Kuznetsov Yu.A. Matrices and computations, Moscow: Nauka, 1984.