Description of algorithm properties and structure
All fundamentally important issues affecting the efficiency of the resulting programs must be reflected in the description of the properties and structure of the algorithms. With this in mind, an algorithm description structure was developed, which formed the basis for the AlgoWiki encyclopedia. The encyclopedia offers standardized elements for different sections and recommendations for building them, so that descriptions of different algorithms could easily be compared.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 2.1 Implementation peculiarities of the serial algorithm
- 2.2 Locality of data and computations
- 2.3 Possible methods and considerations for parallel implementation of the algorithm
- 2.4 Scalability of the algorithm and its implementations
- 2.5 Dynamic characteristics and efficiency of the algorithm implementation
- 2.6 Conclusions for different classes of computer architecture
- 2.7 Existing implementations of the algorithm
- 3 References
1 Properties and structure of the algorithm
Algorithm properties are independent of the computing system, and, in this regard, this part of AlgoWiki is an important thing by itself. An algorithm description is only prepared once; afterwards, it is used repeatedly for implementation within various computing environments. Even though this part is dedicated to the machine-independent properties of algorithms, things to consider during the implementation process or links to respective items in the second part of AlgoWiki are acceptable here.
1.1 General description of the algorithm
This section contains a general description of the problems the algorithm is intended to address. The description shows specific features of the algorithm itself and objects it works with.
1.2 Mathematical description of the algorithm
A mathematical description of the problem to be addressed is presented as a combination of formulas, as it is commonly described in textbooks. The description must be sufficient for an unambiguous understanding of the description by a person who is familiar with mathematics.
1.3 Computational kernel of the algorithm
The computational kernel (the part of algorithm that takes up most of the processing time) is separated and described here. If an algorithm has more than one computational kernel, each one is described separately.
1.4 Macro structure of the algorithm
If an algorithm relies on other algorithms as its constituent parts, this must be specified in this section. If it makes sense to provide the further description of the algorithm in the form of its macro structure, the structure of macro operations is described here. Typical macro operations include finding the sum of vector elements, dot product, matrix-vector multiplication, solving a system of linear equations of small rank, calculating the value of a function at a specific point, searching for the minimum value in an array, matrix transposition, reverse matrix calculation, and many others.
The macro structure description is very useful in practice. The parallel structure for most algorithms is best seen at the macro level, while reflection of all operations would clutter the picture.
The choice of macro operations is not fixed; by grouping macro operations in different ways it is possible to emphasize different properties of the algorithms. In this regard, several macro structure options can be shown here to provide an additional aspect of its overall structure.
1.5 Implementation scheme of the serial algorithm
This section describes the steps that need to be performed in the serial implementation of this algorithm. To a certain degree, this section is redundant, as the mathematical description already contains all the necessary information. However, it is still useful; the implementation of the algorithm is clearly laid out, helping to unambiguously interpret the properties and estimates presented below.
1.6 Serial complexity of the algorithm
This section of the algorithm description shows an estimate of its serial complexity, i.e., the number of operations that need to be performed if the algorithm is executed serially (in accordance with section 1.5). For different algorithms, the meaning of an operation used to evaluate its complexity can vary greatly. This can include operations on real numbers, integers, bit operations, memory reads, array element updating, elementary functions, macro operations, etc. LU factorization is dominated by arithmetic operations on real numbers, while only memory reads and writes are important for matrix transposition; this must be reflected in the description.
For example, the complexity of a vector elements pairwise summation is [math]n-1[/math]. The complexity of fast Fourier transformation (Cooley-Tukey algorithm) for vector lengths equals a power of two - [math]n\log_2n[/math] complex addition operations and [math](n\log_2n)/2[/math] complex multiplication operations. The complexity of a basic Cholesky factorization algorithm (point-structured version for a dense symmetrical and positive-definite matrix) is [math]n[/math] square root calculations, [math]n(n-1)/2[/math] division operations, and [math](n^3-n)/6[/math] multiplication and addition (subtraction) operations each.
1.7 Information graph
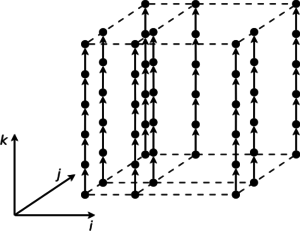
This is a very important part of the description. This is where one can show (see) the parallel structure of the algorithm, for which there is a description and a picture of its information graph [1]. There are many interesting options for reflecting the information structure of algorithms in this section. Some algorithms require showing a maximum-detail structure, while using only the macro structure is sufficient for others. A lot of information is available in various projections of the information graph, which make its regular components stand out, while minimizing insignificant detail.
Overall, the task of displaying an algorithm graph is non-trivial. To begin with, the graph is potentially endless, as its number of vertices and edges is determined by the values of external variables, which can be very large. Situations like this can usually be saved by the "similarity" approach, which makes graphs for different values of an external variable "similar": in most cases it is enough to present a relatively small-sized graph, and the graphs for other values will be "exactly the same". In practice, it isn't always so simple, and one needs to be very careful.
Further, an algorithm graph is potentially a multi-dimensional object. The most natural system for placing the vertices and edges of the information graph is based on the nesting loops in the algorithm implementation. If the nesting loop level does not exceed three, the graph can be placed in the traditional three-dimensional space; more complex loop constructs with a nesting level of 4 or more require special graph display and presentation methods.
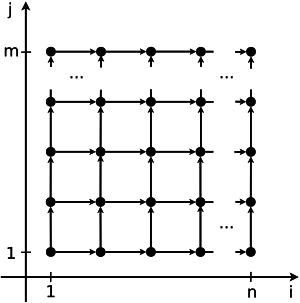
Figures 1 and 2 show the information structure of a matrix multiplication algorithm and of an algorithm for solving a system of linear algebraic equations with a block-structured bidiagonal matrix.
1.8 Parallelization resource of the algorithm
This section shows an estimate of the algorithm's parallel complexity: the number of steps it takes to execute the algorithm assuming an infinite number of processors (functional units, computing nodes, cores, etc.). The parallel complexity of an algorithm is understood as the height of its canonical parallel form [1]. It is necessary to indicate in terms of which operations the estimate is provided. It is also necessary to describe the balance of parallel steps by the number and type of operations, which determines the layer width in the canonical parallel form and the composition of operations within the layers.
Parallelism in algorithms frequently has a natural hierarchical structure. This fact is highly useful in practice and must be reflected in the description. As a rule, such hierarchical parallelism structures are well reflected in the serial implementation of the algorithm through the program's loop profile, which can well be used to reflect the parallelism resource.
Describing the parallelism resource for an algorithm requires specifying key parallel branches in terms of finite and mass parallelism. The parallelism resource isn't always expressed in simple terms, e.g., through coordinate parallelism; the skewed parallelism resource is equally important. Unlike coordinate parallelism, skewed parallelism is much harder to use in practice, but it is an important option to keep in mind, as sometimes it is the only option. A good illustration is the algorithm structure shown in Figure 2: there is no coordinate parallelism, but skewed parallelism is there, and using it reduces the complexity from [math]n\times m[/math] in serial execution to [math](n+m-1)[/math] in the parallel version.
For example, let's look at some algorithms for which serial complexity has been considered in section 1.6. The parallel complexity for vector elements pairwise summation is [math]\log_2n[/math], with the number of operations at each level decreasing from [math]n/2[/math] to [math]1[/math]. The parallel complexity of the fast Fourier transformation (Cooley-Tukey algorithm) for vector lengths equal to a power of two is [math]\log_2n[/math]. The parallel complexity of a basic Cholesky factorization algorithm (point-structured version for a dense symmetrical and positive-definite matrix) is [math]n[/math] steps for square root calculations, [math](n-1)[/math] steps for division operations and [math](n-1)[/math] steps for multiplication and addition operations.
1.9 Input and output data of the algorithm
This section contains a description of the structure, features and properties of the algorithm's input and output data: vectors, matrices, scalars, arrays, a dense or sparse data structure, and their total amount.
1.10 Properties of the algorithm
This section describes other properties of the algorithm that are worth considering in the implementation process. As noted above, there is no connection to any specific computing platform, but since implementation issues always prevail in a project, there is a distinct need to discuss additional properties of an algorithm.
The computational power of an algorithm is the ratio of the total number of operations to the total amount of input and output data. Despite its simplicity, this ratio is exceptionally useful in practice: the higher the computational power, the less the overhead cost of moving data for processing, e.g., on a co-processor, accelerator, or another node within a cluster. For example, the computational power of the dot product operation is [math]1[/math]; the computational power of multiplying two square matrices is [math]2n/3[/math].
The issue of utmost importance is the algorithm stability. Anything related to this notion, particularly the stability estimate, must be described in this section.
The balance of the computing process can be viewed from different perspectives. This includes the balance between different types of operations, particularly arithmetic operations (addition, multiplication, division) together or between arithmetic operations and memory access operations. This also includes the balance of operations between parallel branches of the algorithm.
The determinacy of an algorithm is also important in practice, and it is understood as the uniformity of the computing process. From this point of view, the classical multiplication of dense matrices is a highly deterministic algorithm, as its structure, given a fixed matrix size, does not depend on the elements of the input matrices. Multiplying sparse matrices, where matrices are stored in one or more special formats, is no longer deterministic: data locality depends on the structure of the input matrices. An iteration algorithm with precision-based output is also not deterministic, as the number of iterations (and therefore the number of operations) changes depending on the input data.
A serious issue affecting the indeterminacy of a parallel program is a change in the order of execution for associative operations. A typical example is the use of global MPI operations, e.g., finding the sum of elements in a distributed array. An MPI runtime system dynamically chooses the order of operations, assuming associativity; as a result, rounding errors change between runs, leading to changes in the final output of the program. This is a serious and quite common issue today in massive parallel systems, which translates to lack of reproducible results in parallel program execution. This feature is characteristic for the second part of AlgoWiki, dedicated to algorithm implementations. But the issue is quite important and the respective considerations should be mentioned here as well.
It should be noted that in some cases, a lack of determinacy can be "rectified" by introducing the respective macro operations, which makes the structure both more deterministic and more understandable.
"Long" edges in the information graph are a sign of potential challenges in placing data in the computer's memory hierarchy during the program execution. On the one hand, edge length depends on the specific coordinate system chosen for placing graph vertices, so long as edges can disappear in a different coordinate system (but that can lead to even more long edges appearing elsewhere). On the other hand, regardless of the coordinate system, their presence can signal the need to store data for a long time at a specific hierarchy level, which imposes additional restrictions on the efficiency of the algorithm implementation. One reason for long edges is a scalar value dispersed over all iterations of a specific loop: in this case long edges do not cause any serious issues in practice.
Compact packing of the information graph is of interest in developing specialized processors or implementing an algorithm on FPGAs; it can also be included in this section.
2 Software implementation of the algorithm
The Part II of the algorithm description in AlgoWiki deals with all of the components of the implementation process for an algorithm described in Part I. Both the serial and parallel implementations of an algorithm are considered. This part shows the connection between the properties of the programs implementing the algorithm and the features of the computer architecture they are executed on. Data and computation locality are explained, and the scalability and efficiency of parallel software are described along with the performance achieved with a given program. This is also the place to discuss specific aspects of implementation for different computing architecture classes and to provide references to implementations in existing libraries.
2.1 Implementation peculiarities of the serial algorithm
This section describes the aspects and variations of implementing an algorithm within a serial program that affect its efficiency. In particular, it makes sense to mention the existence of block-structured versions of the algorithm implementation, further describing the prospective advantages and drawbacks of this approach. Another important aspect is related to the options for organizing work with data, variations on data structures, temporary arrays and other similar issues. The required parallelism resource and memory amount for different implementation options need to be specified.
Another important feature is a description of the precision of operations within the algorithm. In practice, it is rarely necessary to perform all arithmetic operations on real numbers with 64-bit floating point arithmetic (double precision), as it doesn't affect the stability of the algorithm or the precision of the results obtained. In this case, if most operations can be performed on a float single precision data, and some fragments require switching to the double, this must be specified here.
Based on information from section 1.8, when describing the serial version of the program, it is worth noting the possibility of equivalent transformaions for programs implementing this algorithm. For example, parallelism of iterations of the innermost loop is normally used for vectorization. However, in some cases this parallelism can be "moved" up the nested loops, which enables more efficient implementation of this algorithm on multi-processor multi-core SMP computers.
2.2 Locality of data and computations
The issues of data and computation locality are rarely studied in practice, but locality is what affects the program execution efficiency on modern computing platforms. This section provides an estimate of data and computation locality in the program, considering both the temporal and spacial locality. Positive and negative locality-related facts should be mentioned, along with what situations could arise under what circumstances. This section also specifies how locality changes when passing from a serial to a parallel implementation. Key patterns in the program's interaction with memory are identified here. Note any possible interrelation between the programming language used and the degree of locality in the resulting programs.
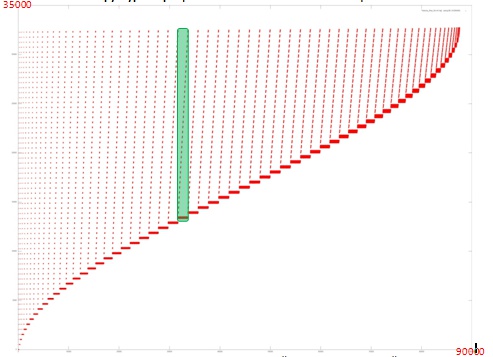
Separately, memory access profiles are specified for computational kernels and key fragments. Figures 3 and 4 show memory access profiles for programs implementing Cholesky factorization and fast Fourier transformation, which illustrates the difference between the locality properties of the two algorithms.
2.3 Possible methods and considerations for parallel implementation of the algorithm
This is a rather big section that must describe key facts and statements that define a parallel program. These can include:
- a hierarchically presented parallelism resource based on the program's loop structure and program call graph;.
- a combination (hierarchy) of mass parallelism and finite parallelism;
- possible ways to distribute operations between processes/threads;
- possible strategies to distribute data;
- an estimate of the number of operations, amount and number of data transfers (both the total number and the share for each parallel process);
- an estimate of data locality, etc.
This section should also include recommendations or comments regarding the algorithm's implementation using various parallel programming technologies: MPI, OpenMP, CUDA, or using vectorization directives.
2.4 Scalability of the algorithm and its implementations
This section is intended to show the algorithm's scalability limits on various platforms. The impact of barrier synchronization points, global operations, data gather/scatter operations, estimates of strong or weak scalability for the algorithm and its implementations.
An algorithm's scalability determines the properties of the algorithm regardless of the computer being used. It shows how much the algorithm enables the computer's actual performance to increase with a potentially infinite increase in the number of processors. The scalability of parallel programs is determined in connection with a specific computer and shows how much the performance of this computer running this program can increase when utilizing more computing power.
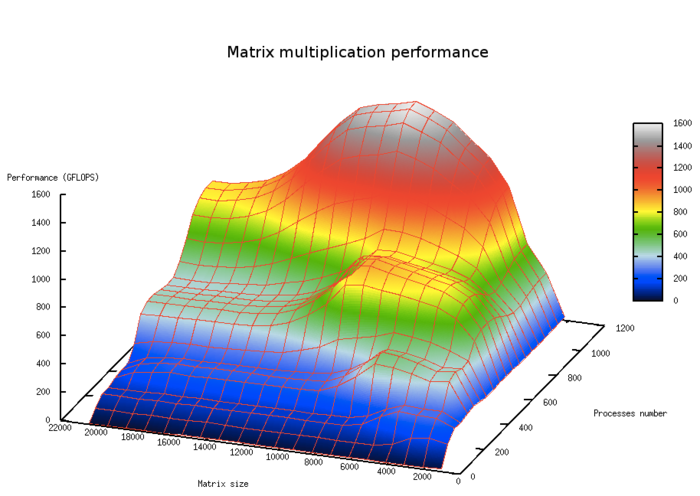
The central idea of this section is to show the actual scalability of the program implementing a given algorithm on various computing platforms, depending on the number of processors and the size of the problem. It is important to choose a proper correlation between the number of processors and the size of the problem, so as to reflect all features in behavior of the parallel program, particularly achieving maximum performance, and more subtle effects arising, for example, from the algorithm's block structure or memory hierarchy.
Figure 5 shows the scalability of a classical matrix multiplication algorithm, depending on the number of processors and the size of the problem. The chart shows visible areas with greater performance, reflecting cache memory levels.
2.5 Dynamic characteristics and efficiency of the algorithm implementation
This is a rather large section of AlgoWiki, as evaluating an algorithm's efficiency requires a comprehensive approach and careful analysis of all steps - from the computer architecture to the algorithm itself. Efficiency is understood rather broadly in this section: this includes the efficiency of program parallelization, and the efficiency of program execution relative to the peak performance of computing systems.
In addition to the actual performance, all major reasons should be described that limit further increase in the performance of a given parallel program on a specific computing platform. This is no simple task, as there is no commonly accepted methodology or respective tools that facilitate such an analysis at the present time. One needs to estimate and describe the efficiency of interaction with the memory subsystem (features of the program's memory access profile), the efficiency of using a resource of parallelism built into the algorithm, the efficiency of using communication networks (features of the communication profile), the efficiency of input/output operations, etc. Sometimes overall program efficiency characteristics are sufficient; in some cases it is important to show lower-level system monitoring data, such as CPU load, cache misses, Infiniband network usage intensity, etc.
2.6 Conclusions for different classes of computer architecture
This section should contain recommendations on implementing the algorithm for various architecture classes. If the architecture of a specific computer or platform has any specific features affecting the implementation efficiency, this must be noted here.
I is important to point out both positive and negative facts with regards to specific classes. Possible optimization techniques or even "tips and tricks" in writing programs for a target architecture class can be described.
2.7 Existing implementations of the algorithm
For many algorithm-computer pairs, good implementations have already been developed which can and should be used in practice. This section is here to provide references to existing serial and parallel implementations of an algorithm that are available for use today. It indicates whether an implementation is open-source or proprietary, what type of license it is distributed under, the distributive location and any other available descriptions. If there is any information on the particular features, strengths and/or weaknesses of various implementations, these can be pointed out here.
3 References
- ↑ Jump up to: 1.0 1.1 Voevodin, V.V., Voevodin, Vl.V.: Parallel computing. BHV-St.Petersburg, 608 p. (in Russian) (2002)