Dijkstra's algorithm
Primary authors of this description: A.N.Daryin.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Dijkstra's algorithm[1] was designed for finding the shortest paths between nodes in a graph. For a given weighted digraph with nonnegative weights, the algorithm finds the shortest paths between a singled-out source node and the other nodes of the graph.
Dijkstra's algorithm (using Fibonacci heaps [2]) is executed in O(m + n \ln n) time and, asymptotically, is the fastest of the known algorithms for this class of problems.
1.2 Mathematical description of the algorithm
Let G = (V, E) be a given graph with arc weights f(e) and the single-out source node u. Denote by d(v) the shortest distance between the source u and the node v.
Suppose that one has already calculated all the distances not exceeding a certain number r, that is, the distances to the nodes in the set V_r = \{ v \in V \mid d(v) \le r \}. Let
- (v, w) \in \arg\min \{ d(v) + f(e) \mid v \in V, e = (v, w) \in E \}.
Then d(w) = d(v) + f(e) and v lies on the shortest path from u to w.
The values d^+(w) = d(v) + f(e), where v \in V_r, e = (v, w) \in E, are called expected distances and are upper bounds for the actual distances: d(w) \le d^+(w).
Dijkstra's algorithm finds at each step the node with the least expected distance, marks this node as a visited one, and updates the expected distances to the ends of all arcs outgoing from this node.
1.3 Computational kernel of the algorithm
The basic computations in the algorithm concern the following operations with priority queues:
- retrieve the minimum element (
delete_min); - decrease the priority of an element (
decrease_key).
1.4 Macro structure of the algorithm
Pseudocode of the algorithm:
Input data:
graph with nodes V and arcs E with weights f(e);
source node u.
Output data: distances d(v) to each node v ∈ V from the node u.
Q := new priority queue
for each v ∈ V:
if v = u then d(v) := 0 else d(v) := ∞
Q.insert(v, d(v))
while Q ≠ ∅:
v := Q.delete_min()
for each e = (v, w) ∈ E:
if d(w) > d(v) + f(e):
d(w) := d(v) + f(e)
Q.decrease_key(w, d(w))
1.5 Implementation scheme of the serial algorithm
A specific implementation of Dijkstra's algorithm is determined by the choice of an algorithm for priority queues. In the simplest case, it can be an array or a list in which search for the minimum requires the inspection of all nodes. Algorithms that use heaps are more efficient. The variant using Fibonacci heaps [2] has the best known complexity estimate.
It is possible to implement the version in which nodes are added to the queue at the moment of the first visit rather than at the initialization stage.
1.6 Serial complexity of the algorithm
The serial complexity of the algorithm is O(C_1 m + C_2n), where
- C_1 is the number of operations for decreasing the distance to a node;
- C_2 is the number of operations for calculating minima.
The original Dijkstra's algorithm used lists as an internal data structure. For such lists, C_1 = O(1), C_2 = O(n), and the total complexity is O(n^2).
If Fibonacci heaps [2] are used, then the time for calculating a minimum decreases to C_2 = O(\ln n) and the total complexity is O(m + n \ln n), which, asymptotically, is the best known result for this class of problems.
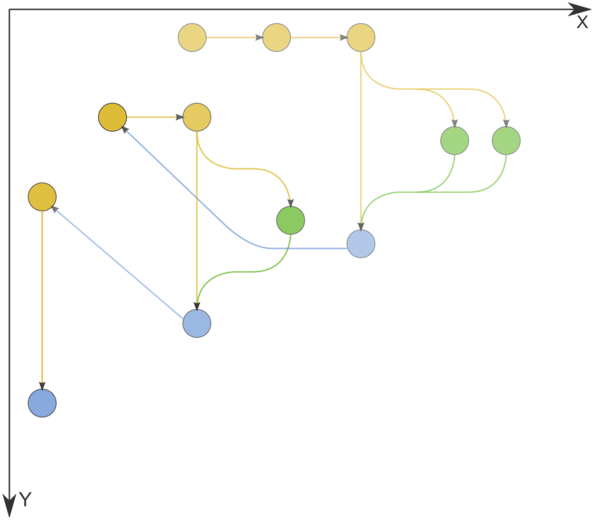
1.7 Information graph
Figure 1 shows the graph of the basic implementation of Dijkstra's algorithm based on lists or arrays.
1.8 Parallelization resource of the algorithm
Dijkstra's algorithm admits an efficient parallelization [3] Its average execution time is O(n^{1/3}\ln n), and the computational complexity is O(n \ln n + m).
The algorithm of Δ-stepping can be regarded as a parallel version of Dijkstra's algorithm.
1.9 Input and output data of the algorithm
Input data: weighted graph (V, E, W) (n nodes v_i and m arcs e_j = (v^{(1)}_{j}, v^{(2)}_{j}) with weights f_j), source node u.
Size of input data: O(m + n).
Output data (possible variants):
- for each node v of the original graph, the last arc e^*_v = (w, v) lying on the shortest path from u to v or the corresponding node w;
- for each node v of the original graph, the summarized weight f^*(v) of the shortest path from u to v.
Size of output data: O(n).
1.10 Properties of the algorithm
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
2.2 Possible methods and considerations for parallel implementation of the algorithm
2.3 Run results
2.4 Conclusions for different classes of computer architecture
3 References
- ↑ Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.
- ↑ Jump up to: 2.0 2.1 2.2 Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1987): 596–615. doi:10.1145/28869.28874.
- ↑ Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.