Horners, locality

Primary author of this description: Vadim Voevodin (part 2).

1 Links

The main fragment of the implementation used to obtain the quantitative estimates is given here (the KernelHorner function).

2 Locality of data and computations

2.1 Locality of implementation

2.1.1 Structure of memory access and a qualitative estimation of locality

Figure 1. Implementation of Horner’s scheme. The general memory-access profile.

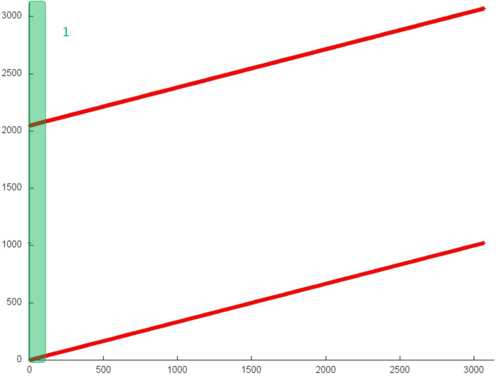
The memory-access profile is illustrated in Fig.1 for a serial implementation of Horner’s scheme in the case of polynomials with real coefficients. From this figure it follows that the structure of this profile is very simple and consists of two linear (or sequential) searches of elements performed for two real arrays in parallel.

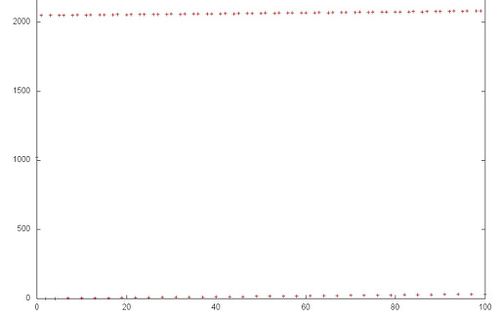
However, this simple example shows that, in order to completely understand a general structure of memory access, it is necessary to carefully analyze this structure at the level of individual memory references. Fig.2 illustrates fragment 1 highlighted in green in Fig.1. As can be seen, the upper sequential search is somewhat different from the lower one: in the first case, each element is referenced twice in succession. Note, however, this refinement of the memory-access profile structure has a little effect on the locality of the entire profile.

On the whole, the general memory-access profile possesses a high spatial locality, since the search of elements in the arrays is performed sequentially. However, the temporal locality is very low, since each element of one of the arrays is referenced only twice, whereas the elements of the second array are not reused at all.

Figure 2. Fragment 1 (the first 100 references of the general profile).

2.1.2 Quantitative estimation of locality

The start conditions are discussed here.

The first estimate is made on the basis of the daps characteristic used to evaluate the number of write and read operations per second. This characteristic is similar to the flops estimate for memory access and is an estimate of the memory usage performance rather than an estimate of locality. However, the daps characteristic is a good information source and can be used to compare with the results obtained according to the cvg characteristic.

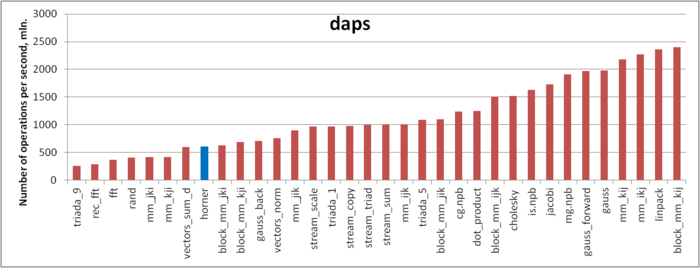
Figure 3 illustrates the daps values for a number of some widespread algorithms. These values are given in increasing order: a higher performance corresponds to a larger daps value. From this figure it follows that the implementation of Horner’s scheme is characterized by a low memory usage performance. It may appear strange that in this case the daps value is significantly less than for the STREAM tests, although the memory-access profiles are similar: several simultaneous sequential searches for the elements of arrays.

Such a behaviour of the implementation under study is caused by the peculiarities of the memory structure. As mentioned above, the elements of one of the arrays are referenced twice in succession. In the source code of the implementation, however, the second reference is performed at the next iteration to the previous element:

for (int i = 1; i < size; i++) {
    c[i] = a[i] + c[i - 1] * x;
}

Hence, we have the case when the iterations are dependent. As a result, the hardware prefetcher badly prefetches the required cache lines, which leads to a significant slowing of the program speed compared to the other implementations based on the sequential search (for example, the STREAM tests).

Our discussion shows once more that the memory structure is very complex: a minor change made in the loop body leads to an unexpectedly serious slowing of the program.

Figure 3. Comparison of daps values.

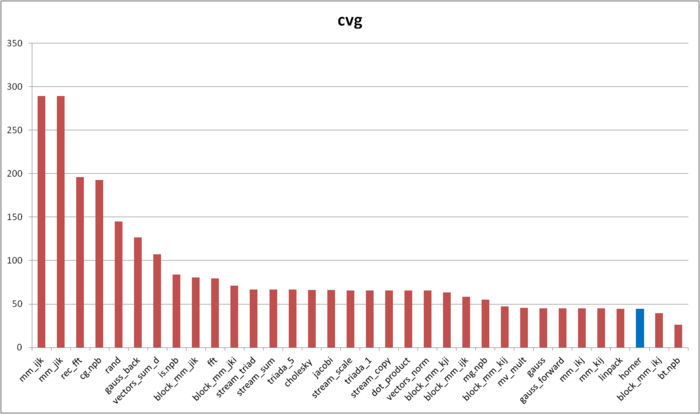
The cvg characteristic is used to obtain a more machine-independent estimate of locality and to specify the frequency of fetching data to the cache memory. A lesser cvg value corresponds to a higher level of locality and to a smaller number of using the fetching procedure.

Fig.4 shows the cvg values for the same implementations presented in Fig.3. These values are given in decreasing order: a higher locality level corresponds to a smaller cvg value. From this figure it follows that the implementation of Horner’s scheme possesses a very high locality according to the cvg estimate.

Figure 4. Comparison of cvg values.

As shown above, this conclusion does not correspond to the actual memory-access performance because of the peculiarities of the memory structure. However, it is necessary to state the following two remarks. First, the cases when the memory-access performance strongly depends on the hardware peculiarities of the memory structure are not very often in practice. Second, the cvg characteristic is used to obtain a machine-independent estimate of locality; hence, it is not possible to take into account such hardware peculiarities when the analysis of memory access is performed in the current framework of discussion.

3 Scalability of the algorithm and its implementations

3.2 Scalability of of the algorithm implementation

Scalability is not analyzed, since Horner’s algorithm is not designed to be implemented in parallel.