Householder (reflections) method for reducing a symmetric matrix to tridiagonal form, SCALAPACK

1 Links

The experiments were conducted for the implementation of the Householder method within the SCALAPACK package of the Intel MKL library (the pdgehrd subroutine).

3 Scalability of the algorithm and its implementations

3.2 Scalability of of the algorithm implementation

Let us study scalability-out for the implementation of this algorithm in accordance with Scalability methodology. This study was conducted using the Lomonosov supercomputer of the Moscow University Supercomputing Center.

Variable start-up parameters for the algorithm implementation and the limits of parameter variations:

• number of processors [16:81] with the step n^2;
• matrix size [1000 : 16000] with the step 1000.

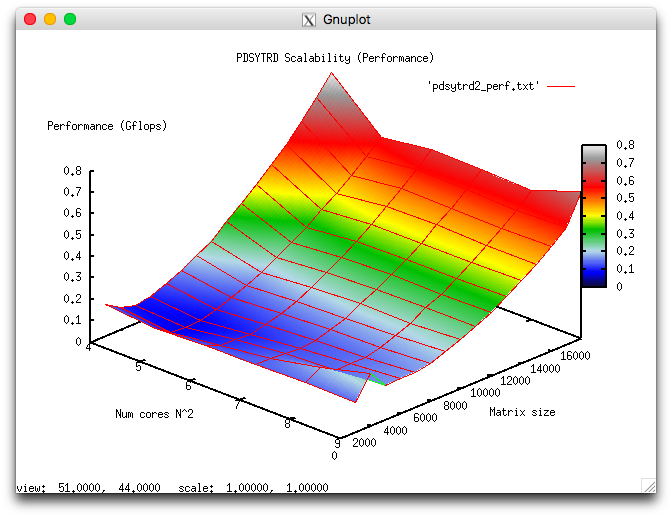
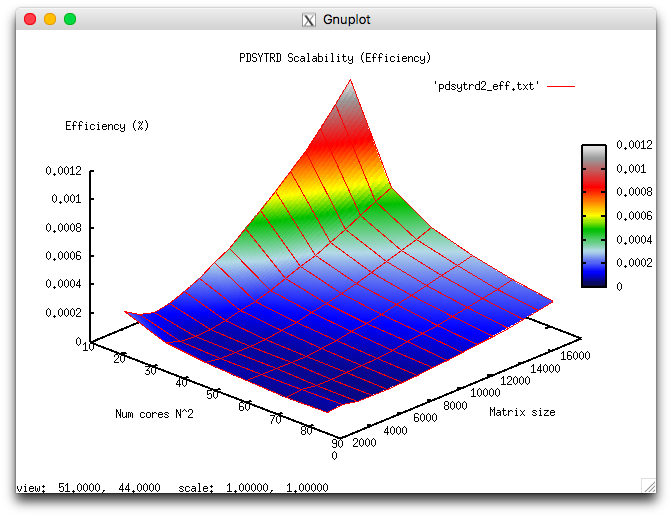
The experiments resulted in the following range of implementation efficiency:

• minimum implementation efficiency 4.763e-05%;
• maximum implementation efficiency 0.011%.

The following figures show the graphs of the performance and efficiency for the Scalapack procedure PDSYTRD as functions of the variable start-up parameters.

Figure 1. Parallel implementation of the Householder (reflection) method. Performance as a function of the number of processors and the matrix size.

Figure 2. Parallel implementation of the Householder (reflection) method. Efficiency as a function of the number of processors and the matrix size.

4 Dynamic characteristics and efficiency of the algorithm implementation

All the results were obtained with the «Lomonosov-2» supercomputer. We used Intel Xeon E5-2697v3 processors, the FDR Infiniband network, and the Intel compiler with the options suggested by Intel MKL Advisor.

The figures illustrate the efficiency of this implementation of the Householder (reflection) method for reducing symmetric matrices to tri-diagonal form. The order of the matrix was 15000, and 81 cores were used for these runs.

Figure 3. Graph of CPU loading while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

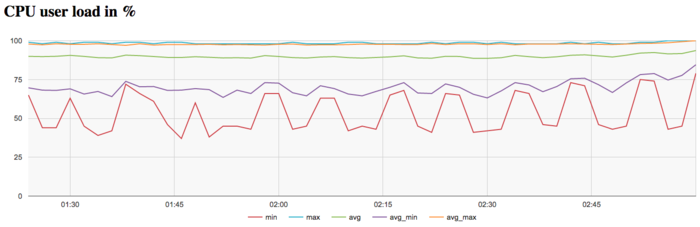
The graph of CPU loading shows that, on the average, the loading is almost all the time about 90 percent. This is a good rate for programs that are run with the use of Hyper Threading technology, that is, all the virtual cores available for this architecture. It is seen that the intensity of calculations is higher at the end of the iteration step compared to the middle part and end of the iteration.

Figure 4. Graph of the number of processes expecting the beginning of the calculation stage (Loadavg) while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

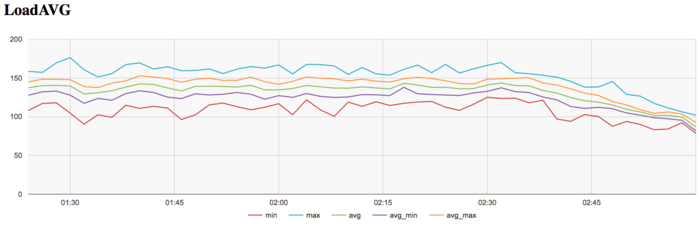
The graph of the number of processes expecting the beginning of the calculation stage (Loadavg) shows that the value of this parameter in the course of the program execution is constant. This value approximately equals to 140 and reduces to 80 only at the end of the iteration step, which indicates that the program performs stably in the course of its execution with 140 threads per node or about 10 threads per physical core at each node. This testifies to a static loading of the hardware resources; however, the number of processes per node is too high, which may indicate that the compilation options are not very reasonable. As a result, the performance may get worse due to overheads for context switching between threads.

Figure 5. Graph of L1 cache misses per second while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

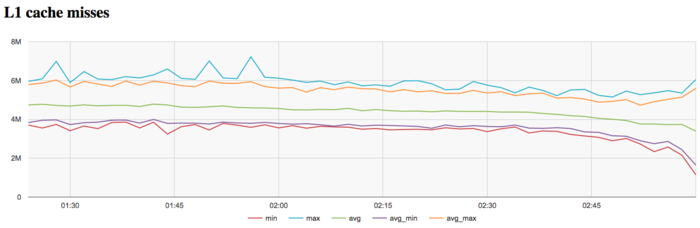
The graph of L1 cache misses shows that the number of misses is rather low. On the average, over all the nodes, it approximately equals to 5 millions per second. It is interesting that the number of misses reduces to the end of iteration. This reduction is not too significant; yet, it is quite noticeable.

Figure 6. Graph of L2 cache misses per second while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

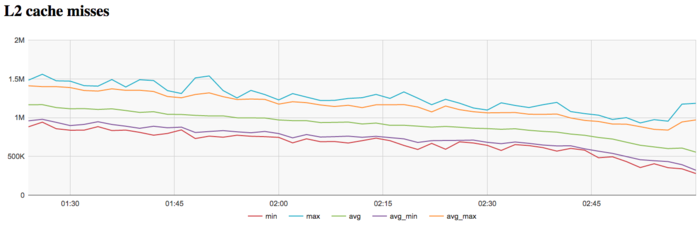
The graph of L2 cache misses shows that the number of these misses is again rather low. On the average, over all the nodes, it approximately equals to 1 million per second. The graph demonstrates more clearly the reduction in the number of misses to the end of iteration. This reduction is more significant and visible (from 1.2 to 0.5 million) compared to L1 cache misses.

Figure 7. Graph of L3 cache misses per second while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

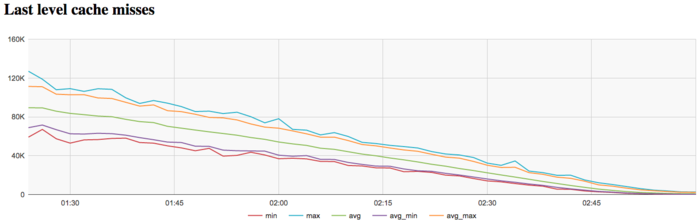
The graph of L3 cache misses shows that the number of these misses is rather low. On the average, over all the nodes, it rapidly decreases from about 90 thousands to 0 per second. This indicates that the problem (especially at the end of iteration) is reasonably matched to the third-level cache memory.

Figure 8. Graph of the data rate through Infiniband network (in bytes per second) while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

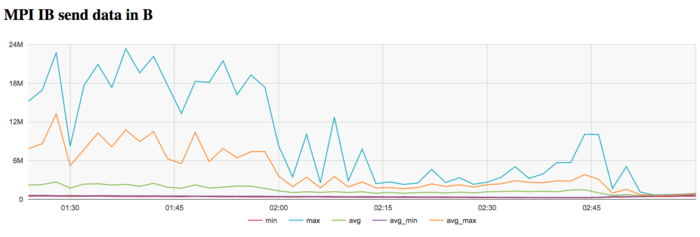
The graph of the data rate through Infiniband network shows that the intensity of use of the communication network is rather low at all iterations. Moreover, the traffic intensity sharply decreases at the end of each iteration. This indicates greater necessity for data exchange between processes at the start of iteration; besides, it shows that the calculations at the end of iteration have reasonable locality.

Figure 9. Graph of the data rate through Infiniband network (in packets per second) while executing the Householder (reflection) method for reducing a matrix to tri-diagonal form

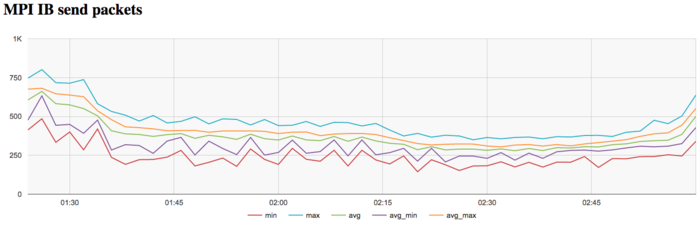
The graph of the data rate measured in packets per second shows that the maximum, minimum, and average values have lower scatter compared to the graph of the data rate measured in bytes per second. This probably says that the processes exchange messages of different length, which testifies to a non-uniform distribution of the data. Moreover, the traffic intensity increases at the end of each iteration. This makes the distinction especially noticeable.

On the whole, according to the data of systemic monitoring, we can make the conclusion that the program worked stably and used the memory efficiently. The use of memory and communication environment is not sufficiently intensive. This may indicate a reduction in efficiency and an increase in performance when the size of the problem grows considerably. Characteristic features of the parallel implementation accomplished in SCALAPACK are sharp decreases in the number of cache misses and data exchanges at the end of iteration.