Householder (reflections) method for reducing a symmetric matrix to tridiagonal form
| The Householder (reflection) method for reducing symmetric matrices to tridiagonal form | |
| Sequential algorithm | |
| Serial complexity | O(n^3) |
| Input data | (n^2+n)/2 |
| Output data | (n^2+3n)/2 |
| Parallel algorithm | |
| Parallel form height | 2n^2+O(n) |
| Parallel form width | n^2/2 |
Primary authors of this description: A.V.Frolov
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
The Householder method (which, in Russian mathematical literature, is more often called the reflection method) is used for bringing real symmetric matrices to tri-diagonal form or, which is the same, for obtaining the decomposition A=QTQ^T (where Q is an orthogonal matrix and T is a symmetric tri-diagonal matrix)[1]. The matrix Q is stored and used not as a full square array but as the product of reflection matrices [2]. Each of these reflections is determined by a vector. For the classical implementation of the reflection method, this makes it possible to store the results of decomposition in place of the matrix A plus additional one-dimensional array.
It is the classical implementation that is discussed here. Techniques like the doubling method for calculating dot products are not used.
1.2 Mathematical description of the algorithm
The Householder method for calculating the QTQ^T decomposition multiplies the current matrix by a Householder (reflection) matrix on the left and then on the right.
The i-th step of the method eliminates the nonzero off-diagonal entries in the i-th column beginning from the i+2-th entry. For this, the left multiplication by a reflection is used. The right multiplication by the same reflection automatically eliminates the nonzero off-diagonal entries in the i-th row beginning from the i+2-th entry; moreover, the resulting matrix recaptures symmetry.
At each step, the reflection is not stored as a conventional square array; instead, it is represented in the form U=E-\frac{1}{\gamma}vv^*, where the vector v is found from the entries of the current i-th column as follows:
Let s be the vector of dimension n+1-i formed of the entries of the i-th column beginning from the i-th entry.
If (s,s)=0, then v=e_{i} and \gamma = \frac{1}{2}.
Otherwise, calculate u = \frac{1}{\sqrt{(s,s)}}s. Then set v_{j}=0 for j \lt i, v_{j}=u_{j-i+1} for j \gt i, and v_{i}=1 if u_{1}=0 and v_{i}=\frac{u_{1}}{|u_{1}|}(1+|u_{1}|), otherwise. Moreover, \gamma = 1+|u_{1}|=|v_{i}|.
After calculating the vector v, one modifies sub-columns located to the right of the pivot column using the formulas x'=x-\frac{(x,v)}{\gamma}v. Then the rows below the pivot row are modified via similar formulas. Using the already calculated vector v and the associativity of operations, one can write out modification formulas for all the entries located to the right of and below the pivot column and row. Suppose that, for each column x^{(j)} indexed by j, we know the number \beta_{j}=\frac{(x^{(j)},v)}{\gamma}. Then the entry of the matrix y in position (i,j) is modified according the formula y' = y - \beta_{i} v_{i} - \beta_{j} v_{j} - \Delta v_{i} v_{j}, where \Delta = \frac{(\beta,v)}{\gamma}. At every step of the algorithm, such modifications for different pairs (i,j) may be performed independently; in particular, they can be carried out in parallel.
1.3 Computational kernel of the algorithm
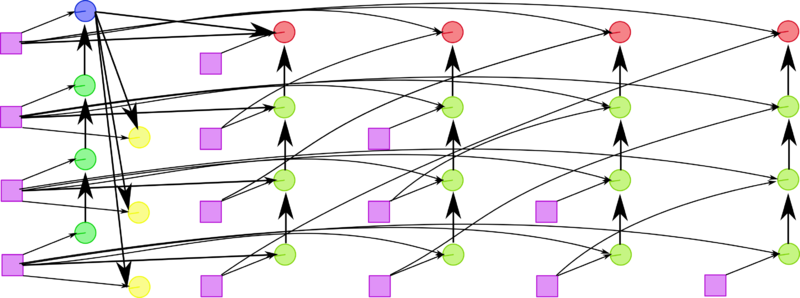
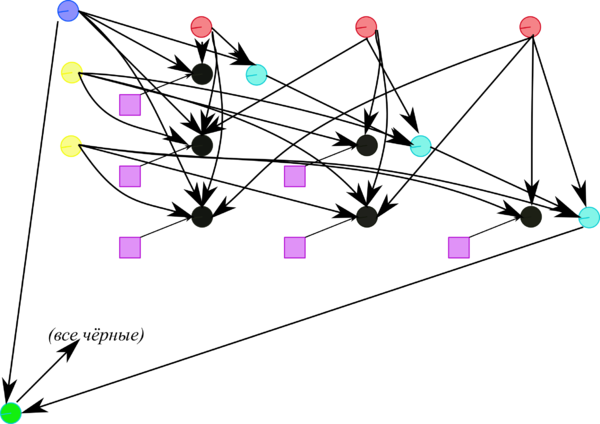
At each step of the algorithm, the bulk of calculations falls on the dot products (s,s) and (x,v) performed for all sub-columns x located to the right of the pivot column, as well as on operations of the type y'=y-ab-cd-fbd performed for the lower right sub-matrix with its symmetry taken into account .
1.4 Macro structure of the algorithm
As already said in the description of the computational kernel, the bulk of calculations falls on the dot products (s,s) and (x,v) performed for all sub-columns x located to the right of the pivot column, as well as on the mass component-wise operations of the type y'=y-ab-cd-fbd. However, the strict order in performing the first two half-steps is not mandatory. The relationship between the vectors s and v makes it possible to calculate the products (x,s) simultaneously with (s,s) and then to express the modification coefficients in terms of these products. This allows us to almost halve the critical path of the algorithm graph.
1.5 Implementation scheme of the serial algorithm
The traditional implementation of the algorithm is a systematic process of eliminating off-diagonal entries in the columns. This process begins from the first column and ends with the penultimate column (that is, column (n-1)).
If the elimination process is applied to column i, then all of its entries with indices from (i+1) to n are eliminated simultaneously.
The elimination in column i consists of two steps: (a) The parameters of reflection U_{i} are calculated. Left multiplication by this reflection effects elimination in column i. (b) The current matrix is simultaneously multiplied by the reflection U_{i} on the left and on the right .
1.6 Serial complexity of the algorithm
The serial complexity of this algorithm is mainly determined by vector dot products, as well as mass modifications of the type y'=y-\alpha v - \beta w - \Delta vw. If we ignore the possible sparsity of the matrix, then these operations require (in the principal term) O(n^3) real multiplications and additions/subtractions.
Therefore, in terms of the number of serial operations, the Householder method should be regarded as a cubic complexity algorithm.
1.7 Information graph
Figures 1 and 2 show the graph of one step of the Householder method in its fastest version (from the viewpoint of parallel implementation). This version uses the fact that, up to a scalar factor, the vector specifying the reflection differs from the sub-column to be eliminated by only a single entry.
1.8 Parallelization resource of the algorithm
Consider the reduction of a symmetric order n matrix to tri-diagonal form by the Householder method. In order to understand the parallelization resource of this method, one needs to inspect the critical path of the corresponding graph.
As is seen from the above description, the elimination in the i-th column involves the calculation of the reflection parameters and certain dot products. These calculations consist of the basic part, which is a branch comprised of 2(n-i) multiplications and additions, and corrections that cost O(1) operations.
Consequently, by a rough estimate (with terms of lower order dropped), the critical path of the Householder method goes through n^2 multiplications and n^2 additions/subtractions.
Hence, operations of the type a+bc take the bulk of execution time both in the serial and parallel versions of the algorithm.
Thus, in terms of the parallel form height, the Householder method is qualified as an algorithm of quadratic complexity. In terms of the parallel form width, it also has quadratic complexity. (If the layers related to vector addition operations were not expanded, then the critical path would be doubled.)
1.9 Input and output data of the algorithm
Input data: dense square symmetric matrix A (with entries a_{ij}).
Size of the input data: (n^2+n)/2.
Output data: tri-diagonal matrix D (in the serial version, the nonzero entries r_{ij} are stored in the positions of the original entries a_{ij}), unitary (or orthogonal) matrix Q stored as the product of Householder matrices (reflections) (in the serial version, their normal vectors to reflection planes are stored in the positions of the original off-diagonal entries a_{ij} and in an additional column of length n).
Size of the output data: (n^2+3n)/2.
1.10 Properties of the algorithm
It is clearly seen that the ratio of the serial to parallel complexity is linear, which yields a certain incentive for parallelization. However, the fastest parallel form has a quadratic width. This indicates an imbalance in the workload of different units when an attempt of actual implementation is made. Even if the computational network is fine (that is, fast), it is more practical to leave the number of units (for instance, cluster nodes) linear with respect to matrix size, which doubles the critical path of the parallel form to be implemented.
The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is linear.
Within the framework of the chosen version, the algorithm is completely determined.
The roundoff errors in the Householder (reflection) method grow linearly, as they also do in the Givens (rotation) method.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
Consider the Householder (reflection) method for reducing a real square symmetric matrix to tri-diagonal matrix in the version with a shortest critical path (which uses the relation between the vector under elimination and the vector that determines reflection). This method can be written in Fortran 77 as follows:
DO I = 1, N-2
DO K = I, N
SX(K)=A(N,I)*A(N,K)
END DO
DO J = N-1, I+1, -1
SX(I)=SX(I)+A(J,I)*A(J,I)
END DO
DO K = I+1, N
DO J = N-1, K, -1
SX(K)=SX(K)+A(J,I)*A(J,K)
END DO
DO J = K-1,I+1,-1
SX(K)=SX(K)+A(J,I)*A(K,J)
END DO
END DO
ALPHA = SQRT (SX(I))
IF (A(I+1,I).NE.0.) THEN
BETA = 1./ALPHA
DO J = I+2, N
A(J,I)=A(J,I)*BETA
END DO
SX(I) = A(I+1,I)*BETA+SIGN(1.,A(I+1,I))
A(I+1,I)=ALPHA
G=1./ABS(SX(I)) ! 1/gamma
SX2=0.
DO K = I+2, N
SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
SX2=SX(K)*A(K,I)+SX2
END DO
SX2=G*SX2
DO K = I+2, N
A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
DO J = K+1, N
A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
END DO
END DO
ELSE
IF (ALPHA.NE.0.) THEN
BETA = 1./ALPHA
DO J = I+2, N
A(J,I)=A(J,I)*BETA
END DO
SX(I) = -1.
A(I+1,I)=ALPHA
G=1.! 1/gamma
SX2=0.
DO K = I+2, N
SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
SX2=SX(K)*A(K,I)+SX2
END DO
SX2=G*SX2
DO K = I+2, N
A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
DO J = K+1, N
A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
END DO
END DO
ELSE
SX(I)=1.
END IF
END IF
END DO
Here, the symmetric tri-diagonal matrix is stored in the locations of the principal diagonal and sub-diagonal of the array A, while the vectors v (without their first components) are stored in the off-diagonal area of this array. The first components are stored in a specially selected array SX.
Usually, in serial versions of the algorithm, the coefficients of column modifications are calculated via dot products after the parameters of reflection have already been found. This slightly simplifies the scheme of the method but extends its critical path. However, this extension is not important for serial realizations.
2.2 Possible methods and considerations for parallel implementation of the algorithm
Most of packages (from LINPACK and LAPACK to SCALAPACK) choose exactly the Householder method (in various modifications, which usually use BLAS) in order to reduce a symmetric matrix to tri-diagonal form. There is a large amount of research devoted to block versions of this method.
2.3 Run results
2.4 Conclusions for different classes of computer architecture
Compared to the Givens method, which has the natural two-dimensional partition based on the pointwise version, the Householder method is adapted for distributed memory systems worse than for shared memory ones. This is due to the fact that the locality is worse (because of the presence of packet distributions) and the number of independent generalized graph scans is smaller. Consequently, on massively parallel distributed memory systems, one should use the Householder method (if its implementation is required) in its block versions instead of the pointwise version. Note that these block versions are independent methods rather than just a block slicing of the pointwise method. The use of block versions is especially recommended when the matrix is very sparse.