Poisson equation, solving with DFT

Primary authors of this description:V.M.Stepanenko, E.V.Mortikov.

1 Properties and structure of the algorithm

1.1 General description of the algorithm

The Poisson equation for the multidimensional space has the form [math] \sum_{i=1}^{N}\frac{\partial^2 \phi}{\partial x_i^2}=f,~\mathbf{x}\in D. [/math]

Here, [math]D \in \mathbb{R}^N[/math] is the domain in which the solution [math]\phi(\mathbf{x})[/math] is defined, and [math]\mathbf{x}=(x_1,...,x_N)^T[/math] is the vector of independent variables. The Poisson equation is supplemented by the boundary conditions [math] B(\phi)=F, \mathbf{x} \in \Gamma(D), [/math] where [math]\Gamma(D)[/math] is the boundary of [math]D[/math] and [math]B(\phi)[/math] is the operator defining the boundary conditions. The case [math]B(\phi)=\phi[/math] corresponds to the Dirichlet boundary condition, while [math]B(\phi)=\partial\phi/\partial n[/math], where [math]\mathbf{n}[/math] is the outer normal to the boundary [math]\Gamma(D)[/math], corresponds to the Neumann boundary condition. Sometimes mixed boundary conditions [math]B(\phi)=C\phi+\partial\phi/\partial n[/math], where [math]C[/math] is a constant, are also used. The so-called "periodic boundary conditions" are also useful in some problems. In this case, the problem is posed on an unbounded domain, but the solution is assumed to be periodic with respect to a subset of variables from [math]\mathbf{x}[/math].

The Poisson equation emerges in many problems of mathematical physics, for instance, in electrostatics (in this case, [math]\phi[/math] is the potential of the electric force) and hydrodynamics ([math]\phi[/math] is the pressure of a fluid or a gas). The parameter [math]N[/math] is 2 and 3 for the plane and three-dimensional problems, respectively.

The analytical form of the solution to the Poisson equation is not known in the case where the right-hand side is arbitrary and the boundary conditions are inhomogeneous. Consequently, in most applications, this equation is solved numerically. The most common discretization of the Poisson equation has the form

[math] \sum_{i=1}^{N}\frac{\phi_{k_1,...,k_i+1,...,k_N}-2\phi_{k_1,...,k_i,...,k_N}+\phi_{k_1,...,k_i-1,...,k_N}}{\Delta x_i^2}=f_{k_1,...,k_N},~(k_1,...,k_N) \in D_N. [/math]

Here, the second derivatives are replaced by second-order finite difference approximations (which creates the cross stencil for the plane problem), and the solution is sought on a discrete subset [math]D_N[/math] of the [math]N[/math]-dimensional space. The boundary conditions are also approximated by finite differences.

1.2 Mathematical description of the algorithm

Here, we examine a finite difference scheme for the most common problem related to the Poisson equation in the three-dimensional space:

[math] \frac{\phi_{i+1,j,k}-2\phi_{i,j,k}+\phi_{i-1,j,k}}{ \Delta x^2}\,+\, \frac{\phi_{i,j+1,k}-2\phi_{i,j,k}+\phi_{i,j-1,k}}{ \Delta y^2}\,+\, \frac{\phi_{i,j,k+1}-2\phi_{i,j,k}+\phi_{i,j,k-1}}{ \Delta z^2} = f_{i,j,k},~(i,j,k) \in D_h, [/math]

where [math]D_h=\{0:N_x-1\}\times\{0:N_y-1\}\times\{0:N_z-1\} [/math] is a parallelepiped in the grid domain. For simplicity, we impose the so-called 3-D periodic boundary conditions

[math] \begin{align} \phi_{0,j,k} &= \phi_{N_x,j,k},\\ \phi_{i,0,k} &= \phi_{i,N_y,k},\\ \phi_{i,j,0} &= \phi_{i,j,N_z}. \end{align} [/math]

The periodic boundary conditions are automatically satisfied if the solution is represented via the conventional discrete inverse Fourier transform:

[math] \phi_{i,j,k}=\frac{1}{N_x N_y N_z}\sum_{l=0}^{N_x-1}\sum_{m=0}^{N_y-1}\sum_{n=0}^{N_z-1}\Phi_{l,m,n}e^{2\pi \overline{i} \left(\frac{il}{N_x}+\frac{jm}{N_y}+\frac{kn}{N_z}\right)}. [/math]

Here, [math]\overline{i}=\sqrt{-1}[/math]. A similar representation is applied to the right-hand side [math]f_{i,j,k}[/math]. The convenience of using the Fourier transform for solving the discrete Poisson equation stems from the fact that the basis functions of the Fourier expansion are eigenfunctions of the discrete Laplace operator. Namely, by substituting the Fourier expansions of the unknown function [math]\phi_{i,j,k}[/math] and the right-hand side [math]f_{i,j,k}[/math] into the original equation, we obtain

[math] \Phi_{l,m,n}=-\frac{F_{l,m,n}}{4\left[\sin^2\left(\frac{\pi l}{N_x}\right) + \sin^2\left(\frac{\pi m}{N_y}\right) + \sin^2\left(\frac{\pi n}{N_z}\right) \right]}, [/math]

where [math]F_{l,m,n}[/math] is the Fourier transform of the right-hand side. This makes obvious the algorithm for solving the equation: first, the right-hand side is expanded into the Fourier series, then the above formula is used for calculating the Fourier coefficients of the solution; finally, the solution is reconstructed by applying the inverse Fourier transform.

1.3 Computational kernel of the algorithm

The one-dimensional Fourier transform is the computational kernel of this algorithm. Indeed, the discrete inverse Fourier transform can be written as

[math] \phi_{i,j,k}=\frac{1}{N_x} \sum_{l=0}^{N_x-1} \left[ e^{2\pi \overline{i}\left(\frac{il}{N_x}\right)} \frac{1}{N_y} \sum_{m=0}^{N_y-1} \left[ e^{2\pi \overline{i}\left(\frac{jm}{N_y}\right)} \frac{1}{N_z} \sum_{n=0}^{N_z-1} \Phi_{l,m,n}e^{2\pi \overline{i} \left(\frac{kn}{N_z}\right)}\right]\right]. [/math]

One can see that the three-dimensional Fourier transform reduces to the sequence of three one-dimensional transforms. A widely used tool for calculating the one-dimensional transform is an efficient algorithm called the fast Fourier transform (FFT) .

1.4 Macro structure of the algorithm

From the above discussion, it is clear that the fast Fourier transform is the basic macro operation in the algorithm for solving the Poisson equation. In what follows, we denote this operation by [math]\text{FFT}_i,~i=x,y,z[/math] in accordance with its direction, while the inverse Fourier transforms are denoted by [math]\text{IFFT}_i,~i=x,y,z[/math].

1.5 Implementation scheme of the serial algorithm

For brevity, we use the following notation for the grid functions: [math]\phi_h=\{\phi_{i,j,k},~(i,j,k) \in D_h\},~F_h=\{F_{l,m,n},~l=0,...,N_x-1,~m=0,...,N_y-1,~n=0,...,N_z-1\}[/math]. A similar notation is used for [math]f_h[/math] and [math]\Phi_h[/math]. Now, the algorithm can be written as follows:

1. Calculate [math]\text{FFT}_x(f_h)[/math]
2. Calculate [math]\text{FFT}_y(\text{FFT}_x(f_h))[/math]
3. Calculate [math]\text{FFT}_z(\text{FFT}_y(\text{FFT}_x(f_h)))=F_h[/math]
4. Find [math]\Phi_h[/math] from [math]F_h[/math]
5. Calculate [math]\text{IFFT}_x(\Phi_h)[/math]
6. Calculate [math]\text{IFFT}_y(\text{IFFT}_x(\Phi_h))[/math]
7. Calculate [math]\text{IFFT}_z(\text{IFFT}_y(\text{IFFT}_x(\Phi_h)))=\phi_h[/math]

It is remarkable that the entire algorithm can be implemented with the use of a single three-dimensional array of size [math]N_x \times N_y \times N_z[/math]. Indeed, the results of one-dimensional Fourier transforms in one direction can be written to the input array, and the resulting array can be used as an input for transform in the next direction, and so on. Operation (4) is an element-wise array modification.

1.6 Serial complexity of the algorithm

If the domain [math]D_h[/math] is a cube, then [math]N_x=N_y=N_z=N=2^k[/math]. Then the complexity of a one-dimensional FFT in any direction is of the order [math]N(\text{log}_2 N)[/math] operations. At each stage, excepting the fourth, one performs [math]N^2[/math] one-dimensional FFTs, while the number of operations at stage 4 is [math]N^3[/math] (again in order). Thus, the overall number of arithmetic operations is [math]N^3(6\text{log}_2 N+1)[/math].

1.7 Information graph

We present the information graph only for stages 1-4 because stages 5-7 are implemented analogously to stages 1-3.

Green rectangles denote one-dimensional sections of the input three-dimensional array. Red circles denote one-dimensional FFTs; for instance, [math]FFT_{x11}[/math] means that the FFT is performed along the axis x for [math]j=1,~k=1[/math]. Yellow circles denote the element-wise array transformations for calculating the Fourier coefficients of the solution (stage 4 of the algorithm). For example, the symbol [math]L_{2N,1,...,N}[/math] denotes an update of the entries [math]i=2,~j=N,~k=1,...,N[/math]. For convenience, we use the numbers [math]1,...,N[/math] rather than [math]0,...,N-1[/math] as the values of integer indices

The information dependence between the layers of the graph can be stated as follows. A one-dimensional FFT depends on the results of an earlier FFT in a perpendicular direction (which was performed at a previous layer) only if the one-dimensional sections processed by these FFTs intersect each other. Consequently, each [math]FFT_{i,y,k},~i=1,...,N[/math], with respect to the second coordinate depends on the results of each [math]FFT_{x,j,k},~j=1,...,N[/math], w.r.t. the first coordinate if and only if these transformations are executed in the same plane [math]k=K[/math]. Accordingly, each [math]FFT_{i,j,z},~j=1,...,N[/math], w.r.t. the third coordinate depends on each [math]FFT_{i,y,k},~k=1,...,N[/math], w.r.t. the second coordinate if they belong to the same plane [math]i=I[/math].

1.8 Parallelization resource of the algorithm

One can distinguish at least two levels of parallelism in the above algorithm. First, the execution of each one-dimensional FFT can be distributed between computational cores. Second, at each stage of the algorithm (that is, at each layer of the graph), one-dimensional FFTs are independent of each other and can be performed in parallel (coordinate parallelism). In order to compare the parallel complexity (under coordinate parallelization) and the serial one, we take the one-dimensional FFT and the element-wise updating of the array (stage 4 of the algorithm) as the basic operations. Then the serial algorithm consists of [math]6N^2[/math] one-dimensional FFTs, executed sequentially, and [math]N^3[/math] operations over individual array entries. As for the parallel algorithm, it performs 6 steps of one-dimensional FFTs and one step of element-wise modification. By expressing the macro operations introduced above in terms of elementary arithmetic operations, we conclude that the complexity of the serial algorithm is [math]6N^3(\text{log}_2N)+N^3[/math] operations, whereas the complexity of the parallel algorithm is [math]6N(\text{log}_2N)+1[/math] operations. It follows that, for large [math]N[/math], the ratio of the serial to parallel complexity tends to [math]\propto N^2(6\text{log}_2N \text{ln}2+\text{ln}2+5)[/math].

1.9 Input and output data of the algorithm

The right-hand side of the equation delivered as a three-dimensional array of size [math]N \times N \times N[/math] is the input of the algorithm, while the solution stored in a three-dimensional array of the same size is its output.

1.10 Properties of the algorithm

As shown above, the computational complexity of the parallel algorithm decreases faster than [math]N^2[/math] if the number of computing units is unlimited and the input data are voluminous.

Since the size of the input data is [math]N^3[/math], the computational power of the serial algorithm is [math]6\text{log}_2N+1[/math], while the computational power of the parallel algorithm is [math](6N\text{log}_2N+1)/N^3 \propto N^{-2}[/math] (for large [math]N[/math]).

2 Software implementation of the algorithm

2.1 Implementation peculiarities of the serial algorithm

Here, we provide an example of Fortran-90 implementation with the use of the FFTW library. In this case, the direct three-dimensional Fourier transform of the right-hand side is performed as the sequence of three one-dimensional FFTs (stages 1-3 in section 1.5). The resulting Fourier coefficients are divided by the eigenvalues of the Laplace operator (stage 4 in section 1.5) (see the comments in the code):

         ! x - transform
         do k = 1, k1
           do j = 1, j1
             workfor_x(1:i1) = cmplx(f_r(1:i1,j,k),f_i(1:i1,j,k))
             call FFTW_EXECUTE_DFT(planfor_x,workfor_x,workfor_x)
             f_r(1:i1,j,k) = real(real (workfor_x(1:i1)) )
             f_i(1:i1,j,k) = real(aimag(workfor_x(1:i1)) )
           enddo
         enddo
         ! y - transform
         do k = 1, k1
           do i = 1, i1
             workfor_y(1:j1) = cmplx(f_r(i,1:j1,k),f_i(i,1:j1,k))
             call FFTW_EXECUTE_DFT(planfor_y,workfor_y,workfor_y)
             f_r(i,1:j1,k) = real(real (workfor_y(1:j1)) )
             f_i(i,1:j1,k) = real(aimag(workfor_y(1:j1)) )
           enddo
         enddo
         ! z - transform and divide by eigenvalue
         do j = 1, j1
           do i = 1, i1
            workfor_z(1:k1) = cmplx(f_r(i,j,1:k1),f_i(i,j,1:k1))
             call FFTW_EXECUTE_DFT(planfor_z,workfor_z,workfor_z)
             f_r(i,j,1:k1) = real(real (workfor_z(1:k1)) )
             f_i(i,j,1:k1) = real(aimag(workfor_z(1:k1)) )
             ! Divide by eigenvalue of Laplace operator
             sinx = sin((i-1) * Pi / i1)^2 * 4
             siny = sin((j-1) * Pi / j1)^2 * 4
             do k = 1, k1
               sinz = sin((k-1) * Pi / k1)^2 * 4
               f_r(i,j,1:k1) = f_r(i,j,1:k1)/(sinx + siny + sinz)
               f_i(i,j,1:k1) = f_i(i,j,1:k1)/(sinx + siny + sinz)
             enddo
           enddo
         enddo

As soon as the Fourier coefficients have been found, the inverse Fourier transform is performed in a similar way:

         ! inverse x - transform
         do k = 1, k1
           do j = 1, j1
             workback_x(1:i1) = cmplx(f_r(1:i1,j,k),f_i(1:i1,j,k))
             call FFTW_EXECUTE_DFT(planback_x,workback_x,workback_x)
             f_r(1:i1,j,k) = real(real (workback_x(1:i1)) )/real(i1)
             f_i(1:i1,j,k) = real(aimag(workback_x(1:i1)) )/real(i1)
           enddo
         enddo
         ! inverse y - transform
         do k = 1, k1
           do i = 1, i1
             workback_y(1:j1) = cmplx(f_r(i,1:j1,k),f_i(i,1:j1,k))
             call FFTW_EXECUTE_DFT(planback_y,workback_y,workback_y)
             f_r(i,1:j1,k) = real(real (workback_y(1:j1)) )/real(j1)
             f_i(i,1:j1,k) = real(aimag(workback_y(1:j1)) )/real(j1)
           enddo
         enddo
         ! inverse z - transform
         do j = 1, j1
           do i = 1, i1
             workback_z(1:k1) = cmplx(f_r(i,j,1:k1),f_i(i,j,1:k1))
             call FFTW_EXECUTE_DFT(planback_z,workback_z,workback_z)
             f_r(i,j,1:k1) = real(real (workback_z(1:k1)) )
             f_i(i,j,1:k1) = real(aimag(workback_z(1:k1)) )
           enddo
         enddo

One can see that the way in which the loops are embedded corresponds to the column-wise arrangement of the array entries in Fortran. This makes it possible to significantly reduce the memory access time. The same auxiliary arrays are repeatedly used, which should ensure the fast interaction with the cache for grids of modest size. However, this implementation is not optimal. For instance, instead of repeatedly calling the subroutine FFTW_EXECUTE_DFT, a subroutine performing the prescribed set of one-dimensional FFTs could be called just once.

The above program listings make also obvious the parallelization resource of the algorithm; namely, all the one-dimensional Fourier transforms are executed independently of each other. The simplest way to take advantage of this fact is to insert the corresponding OpenMP instructions before the inner loops, provided that a shared memory multicore computer is used. If the program is executed on a distributed memory cluster, then one should make sure that the input array, containing the right-hand side, is distributed between the processors and intermediate arrays are transposed when transiting from the FFT in one direction to that in the other.

Note that, for performing one-dimensional FFTs, the above implementation calls a procedure from the FFTW library that processes arrays of complex numbers. On the other hand, there are specific FFT routines for processing real arrays and they are twice as fast as the complex algorithm (for more details, see the the FFTW project site ([1]).

An important circumstance is the fact that most variants of FFT, including the Cooley-Tukey algorithm, have very low errors when performed in floating point arithmetic. The relative error of the Cooley-Tukey algorithm is bounded from above by [math]O(\epsilon \log N)[/math]. (For comparison, note that the straightforward implementation via the formulas of the discrete Fourier transform has the relative error [math]O(\epsilon N^{3/2})[/math].) . Thus, one can accelerate the algorithm by using single precision floating point numbers, with no significant error increase.

2.2 Possible methods and considerations for parallel implementation of the algorithm

As shown above, there are at least two levels of parallelism in the algorithm under discussion. The first level concerns the parallel implementation of a one-dimensional FFT, while the second level is the coordinate parallelism, that is, a parallel execution of independent one-dimensional FFTs . These two levels can be combined; for instance, different FFTs can be distributed between MPI processes, while each individual FFT can be distributed between threads with shared memory (POSIX, OpenMP, etc.). Below, we present some details of the base parallelization algorithm using the coordinate parallelism, discuss its shortcomings, and list possible ways of improving its scalability.

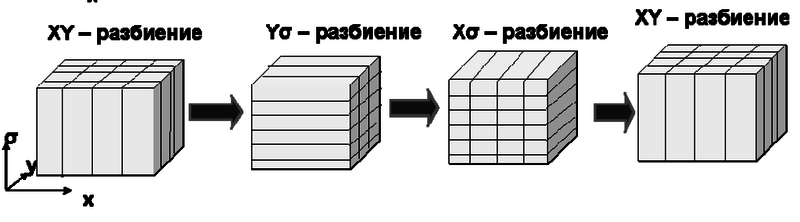
In the context of this problem, the coordinate parallelism is realized by decomposing a three-dimensional domain into subdomains. In such subdomains, one-dimensional FFTs can be performed independently of each other. Presently, two implementations of this approach are available. They are one-dimensional domain decomposition (slab decomposition) and two-dimensional decomposition (pencil decomposition) . Under one-dimensional decomposition, one requires a smaller number of MPI-Sends; however, the maximum number of processes/cores is bounded by the maximum (over three dimensions) size of the domain. Consequently, from the viewpoint of massive parallelism, two-dimensional decomposition is preferable. In what follows, we discuss exactly this approach.

Under MPI implementation, one must take into account the overhead expenses caused by data transfers between processors. The algorithm under discussion also requires that the so-called array transpositions be performed. At each of the three stages of Fourier transforms (stages 1-3 and 5-7 in section 1.5), these transpositions ensure finding the array entries along the corresponding direction in the memory of the corresponding processor.

Transposition of a three-dimensional array under a parallel implementation of the three-dimensional FFT

Consider the relation between calculations and data transfers under MPI implementation. Suppose that the coordinate parallelization for [math]M[/math] MPI processes is used. Then the computational complexity of the algorithm is [math] \left(6N^3(\log_2 N) + N^3\right)/M[/math], which is at the best [math] 6N(\log_2 N) + N[/math] (if [math]N^2[/math] processes are employed). The total amount of MPI packages (sent and received) is [math]8N_{px}+4N_{py}[/math], while the total amount of array entries (sent and received) is [math]12N^3/(N_{px}N_{py})[/math] for each process (here, [math]N_{px},~N_{py}[/math] are the numbers of processes along the axes [math]x[/math] and [math]y[/math], respectively, for the two-dimensional MPI decomposition used; see the above figure). Since [math]M=N_{px}N_{py}[/math], we conclude that the ratio "the number of forwarded array entries to the number of arithmetic operations" is [math]\alpha=12/(6\log_2 N + 1)[/math]. Thus, the ratio "the amount of data traffic to the number of operations" is independent of the number of MPI processes, and this ratio decreases with the growth in the problem size. However, the decay becomes slow for large [math]N[/math] (the saturation phase). On the other hand, consider the case of a fixed problem size. Then an increase in the number of processes does not alter the parameter [math]\alpha[/math], but it causes an increase in the number of packages ([math]\propto \sqrt{M}[/math], in view of [math]N_{px} \propto N_{py} \propto \sqrt{M}[/math] and the above formulas). Due to the network latency, this increases the time for transferring data; consequently, the acceleration of the algorithm slows down.

The above analysis can only serve for approximate estimates because no times for computation and MPI exchanges were given. More detailed calculations for one- and two-dimensional domain decompositions are abundant in the literature .

In the following sections, we profile the parallel code of this algorithm. In this code, calls of one-dimensional FFTs in three directions shown in the listing in section 2.1 alternate with calls on special procedures performing array transpositions. The real and imaginary parts of an array are transposed separately (which is not optimal because better results are obtained by sending complex numbers) with the use of point-to-point communications. Asynchronous forwarding based on MPI_ISEND and MPI_IRECV is used.