Single-qubit transform of a state vector

Single-qubit transform of a state vector
Sequential algorithm
Serial complexity	[math]3 \cdot 2^n[/math]
Input data	[math]2^n+4[/math]
Output data	[math]2^n[/math]
Parallel algorithm
Parallel form height	[math]2[/math]
Parallel form width	[math]2^{n+1}[/math]

Primary authors of this description: A.Yu.Chernyavskiy.

1 Properties and structure of the algorithm

1.1 General description of the algorithm

The algorithm simulates an action of a single-qubit quantum gate on a state vector.

The operations with small number of qubits (quantum bits) are the basis of quantum computations. Moreover, it's known, that arbitrary quantum computation can be represented by only single- and two-qubit operations. Such operations are the analogues of simple classical logic operations (like NOT, AND, XOR, etc), but have some serious differences, which lead to the simulation difficulties. The main difference is in the fact that even single-qubit operation affects all other qubits due to the phenomena of quantum entanglement. Such "non-locality" gives the huge computational power to the quantum computers, but makes it very difficult to simulate them.

The algorithm of single-qubit transform simulation is often a subroutine and is used iteratively to the different qubits of a state. For example, it's used for the quantum algorithms simulation and the analysis of quantum entanglement. As for the most of the classical algorithms in quantum information science, the described algorithm shows the exponential data growth with respect to the number of qubits. This fact leads to the necessity of a supercomputer usage for the practically important tasks.

1.2 Mathematical description of the algorithm

Input data:

Integer parameters [math]n[/math] (the number of qubits) and [math]k[/math] (the number of the affected qubit).

A complex [math]2 \times 2[/math] matrix [math]U = \begin{pmatrix} u_{00} & u_{01}\\ u_{10} & u_{11} \end{pmatrix}[/math] of a single-qubit transform.

A complex [math]2^n[/math]-dimensional vector [math]v,[/math] which denotes the initial state of a quantum system.

Output data: the complex [math]2^n[/math]-dimensional vector [math]w,[/math] which corresponds to the quantum state after the transformation.

The single-qubit transform can be represented as follows:

The output state after the action of a transform [math]U[/math] on the [math]k-[/math]th qubit is [math]v_{out} = I_{2^{k-1}}\otimes U \otimes I_{2^{n-k}},[/math] where [math]I_{j}[/math] is the [math]j-[/math]dimensional identity matrix, and [math]\otimes[/math] denotes the tensor (Kronecker) product.

However, the elements of the output vector can be represented in more computationally useful direct form:

[math] w_{i_1i_2\ldots i_k \ldots i_n} = \sum\limits_{j_k=0}^1 u_{i_k j} v_{i_1i_2\ldots j_k \ldots i_n} = u_{i_k 0} v_{i_1i_2\ldots 0_k \ldots i_n} + u_{i_k 1} v_{i_1i_2\ldots 1_k \ldots i_n} [/math]

A tuple-index [math]i_1i_2\ldots i_n[/math] denotes the binary form of an array index.

1.3 The computational kernel of the algorithm

The computational kernel of the single-qubit transform can be composed of [math]2^n[/math] calculations of the elements of the output vector [math]w.[/math] The computation of each element consists of two complex multiplication and one complex addition opearations. Moreover we need to compute an indexes [math]i_1i_2\ldots 0_k \ldots i_n,[/math] and the [math]i_k[/math] bits, these computations needs the bitwise operations.

1.4 Macro structure of the algorithm

As noted in the description of the computational kernel, the main part of the algorithm consists of the independent computations of the output vector elements.

1.5 Implementation scheme of the serial algorithm

For [math]i[/math] from [math]0[/math] to [math]2^n-1[/math]

1. Calculate the element [math]i_k[/math] of the binary representation of the index [math]i.[/math]
2. Calculate indexes [math]j[/math] with binary representation [math]i_1i_2\ldots \overline{i_k} \ldots i_n,[/math] where the overline denotes the bit-flip.
3. Calculate [math]w_i = u_{i_k i_k}\cdot v_{i} + u_{i_k \overline{i_k}}\cdot v_j.[/math]

1.6 Serial complexity of the algorithm

The following number of operations is needed for the single-qubit transform:

1. [math]2^{n+1}[/math] complex multiplications;
2. [math]2^n[/math] complex additions;
3. [math]2^n[/math] [math]k[/math]-th bit reads;
4. [math]2^n[/math] [math]k[/math]-th bit writes.

Note, that the algorithm are often used iteratively, that's the the bit operations (3-4) can be performed once in the beginning of computations. Moreover, they can be avoided by the usage of additions and bitwise multiplications with the [math]2^k,[/math] that can be also calculated once for each [math]k.[/math]

1.7 Information graph

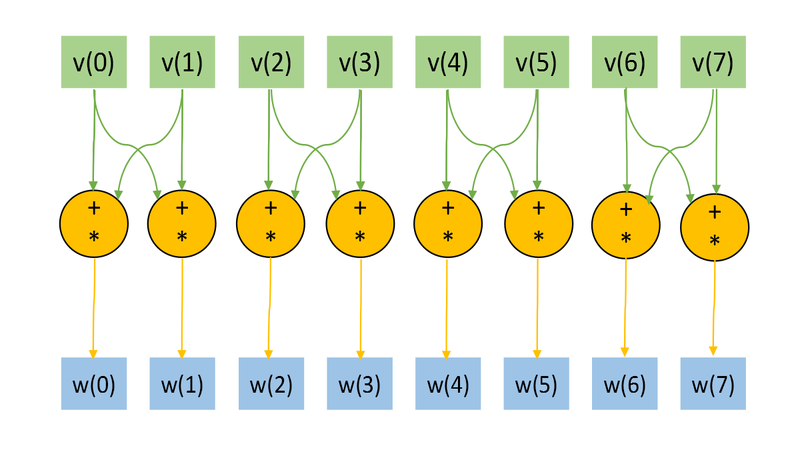
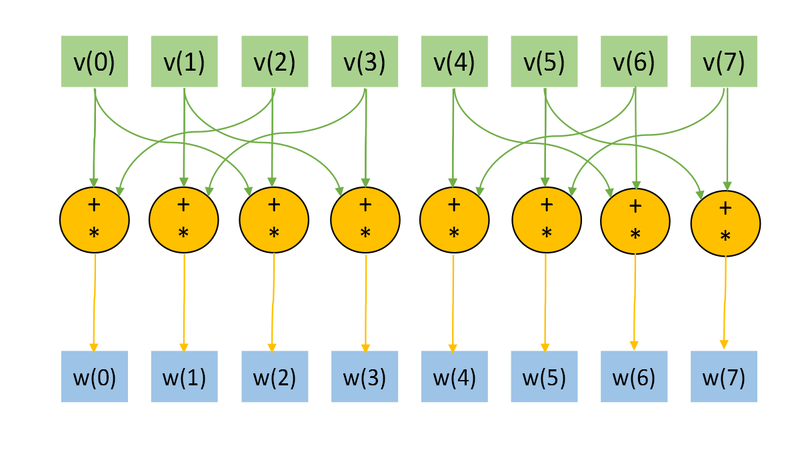
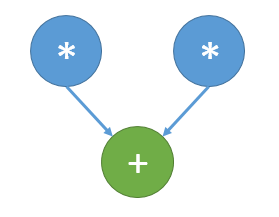
The Figs. 1 and 2 shows the information graph for the paramters [math]n=3, k=1[/math] and [math]n=3, k=2.[/math] The graphs are presented without a transformation matrix [math]U,[/math] because its small size in comparison with a input and output data. Fig.3 shows the main operation, which is denoted by orange on Figs.1-2.

The representation with an input and data and the "folded" triple operation is useful for the understanding of the memory locality. Note, the the structure of an information graph strongly depends on the parameter [math]k.[/math]

Figure 1. The information graph for [math]n=3, k=1[/math] without transformation matrix [math]U.[/math]

Figure 2. The information graph for [math]n=3, k=2[/math] without transformation matrix [math]U.[/math]

Figure 3. The information graph of the main operation.

1.8 Parallelization resource of the algorithm

As we can see on the information graph, the direct algorithm of one-qubit transform simulation has the very high parallelization resource, because all computations of different output vector elements can be made independently. Two multiplication operations needed for the computation of each output vector element also can be done in parallel.

So, there are only two levels of computations:

1. [math]2^{n+1}[/math] multiplications.
2. [math]2^n[/math] additions.

1.9 Input and output data of the algorithm

Input data:

• [math]2^n[/math]-dimensional complex state vector [math]u.[/math] In most cases thу vector is normalized to 1.
• [math]2[/math]-dimensional unitary matrix [math]U[/math].
• The number (index) of the affected qubit [math]q[/math].

Output data:

• The [math]2^n[/math]-dimensional complex output state vector [math]w.[/math].

Amount of input data: [math]2^n+4[/math] complex numbers and [math]1[/math] integer parameter.

Amount of output data: [math]2^n[/math] complex numbers.

1.10 Properties of the algorithm

The ratio of the serial complexity to the parallel complexity is exponential (an exponent transforms to a constant).

The computational power of the algorithm considered as the ratio of the number of operations to the amount of input and output data is constant.

2 Software implementation of the algorithm

2.1 Implementation peculiarities of the serial algorithm

The function of the single-qubit transform may be represented in C language as:

void OneQubitEvolution(complexd *in, complexd *out, complexd U[2][2], int nqubits, int q)
{
	//n - number of qubits
        //q - index of the affected qubit

	int shift = nqubits-q;
	//All bits are zeros, except the bit correspondent to the affected qubit.  
	int pow2q=1<<(shift);

	int N=1<<nqubits;
	for	(int i=0; i<N; i++)
	{
		//Making the changing bit zero
		int i0 = i & ~pow2q;
		
		//Setting the changing bit value
		int i1 = i | pow2q;
		
		//Getting the changing bit value
		int iq = (i & pow2q) >> shift;

		out[i] = U[iq][0] * in[i0] + U[iq][1] *in[i1];
	}
}

Note, that the huge part of the computation and code logic consists of the bit operations, but this can be avoided. In most cases, single-qubit transform is just as a subroutine and is used sequentially many times. Moreover, indexes i0, i1, and iq depends only on the parameters n and q. The n is fixed, and we can calculate these indexes in the beginning of computations for every parameter q, and we need only 3n integers to store the data, when the input and output data growths exponentially. It's obvious that such optimization is critically needed for the implementations of the algorithm for the hardware and software with slow bit operations (for example, Matlab).

2.2 Possible methods and considerations for parallel implementation of the algorithm

The main method of the parallelization is obvious: we need to parallelize the main loop (independent computations of the elements of the output vector), and possibly parallelize in-loop multiplications, which are independent too, as can bee seen from Fig.3. For shared memory systems such method leads to the near ideal speed-up. However, for the distributed memory machines the algorithm has the unsolvable problems with data transfer, that can be seen (for example, from Fig. 8), for big tasks (with the big number of qubits n), the the amount of transfer operations becomes comparable to the arithmetical operation. The possible particular solution is the usage of caching or different programming paradigms like SHMEM. But such unlocality makes it impossible to achieve ideal efficiency on distributed memory machines.

The algorithm is implemented (mostly serial versions) in different libraries for quantum information science and quantum computer simulation. For example: QLib, libquantum, QuantumPlayground, LIQUiD.

2.4 Conclusions for different classes of computer architecture

Because of the very high parallelization possibility, but low locality, the effective and good scalable parallel implementation of the algorithm can be achieved for the shared memory. But the usage of distributed memory leads to the efficiency problems and necessity of special tricks for the optimization. It may be noted, that this task is a very good test platform for the development of methods for the data intense tasks with bad locality.