Single-qubit transform of a state vector, locality
Primary author of this description: Vad.V.Voevodin (Section 2).
Contents
1 Links
The main implementation fragment, which is used in all quantitative assessments, is shown here(Kernel function).
2 Locality of data and computations
Despite of the great parallelization resource, practical implementations have a bad locality.
From the mathematical description and information graphs for the different parameter q (the number of affected qubit), we can see for the single work of the algorithm it's easy to achieve the ideal locality by the permutation of qubits. Thus, if we move the q-th qubit to the last place, we achieve the sequential transfers only between local elements.
However, the single-qubit transform is almost always used sequentially as a subroutine on a common state with different parameter q. As we can see from the mathematical description and Figs. 1-2, it is impossible to achieve good locality.
2.1 Locality of implementation
2.1.1 Structure of memory access and a qualitative estimation of locality
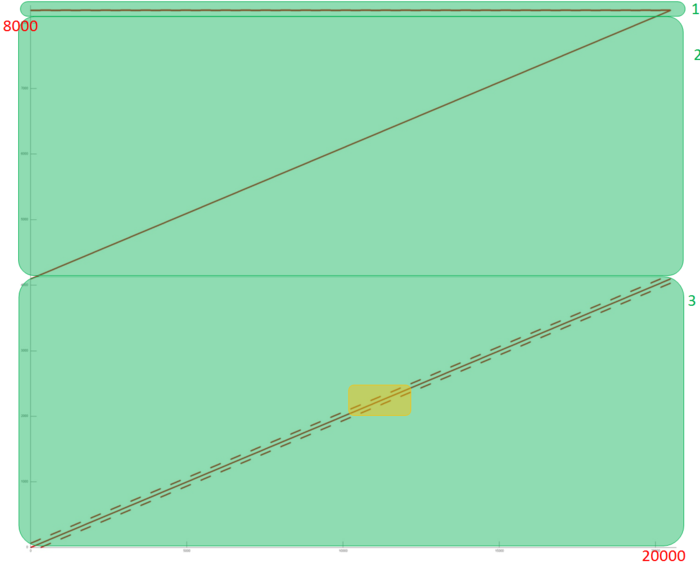
As it was mentioned above, the locality of computations depends on the parameter q (the index of the affected qubit). Firstly, let's examine the memory access for the fixed parameter q (n=12, q=6). A memory access profile is illustrated in Fig. 4. The profile consists of the accesses to three different arrays, these arrays are emphasized on Fig. 4 by the green color. We can see that for the fragmets 2 and 3 memory accesses don't repeat, but the are closely situated. Let's examine the fragments closely.
The fragment 1 is shown on Fig. 5. This array corresponds to the transformation matrix and consists only of 4 elements, so the locality is very high.
The fragment 2 (Fig. 5) shows the simple sequential access to all the array elements. Such fragment has very high spatial and very low time locality (data isn't accessed repeatedly).
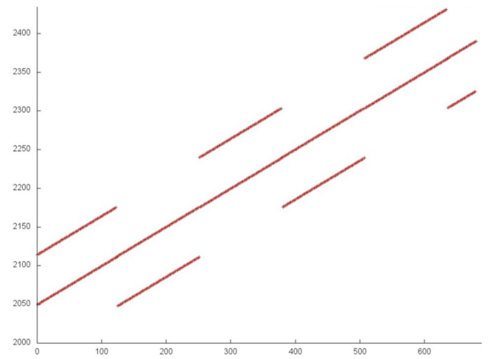
The fragment 3 is most interesting. Its part is shown on Fig. 7. Here we can see again the sequential access to the array elements, but with parallel access to elements with higher or lower virtual addresses.
Now, let's examine the dependence of the memory-access profile on the parameter q (the number of affected qubit). Fig. 8 shows the profile for different values of the parameter. As we can see, the fragments 1 and 2 don't change, but the third fragment change its shift for the parallel access. This makes it difficult to effectively implement the algorithm for the distributed memory.
2.1.2 Quantitative estimation of locality
Launch conditions are described here. The number of qubits was n=24 and the index of affected qubit was q=12.
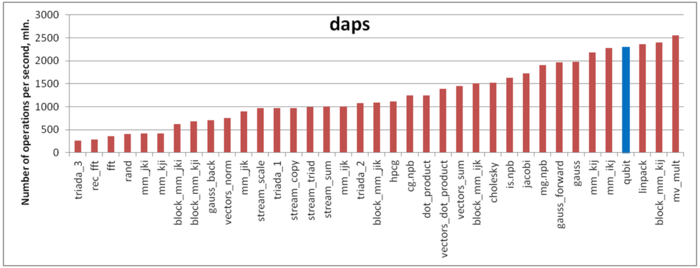
The first estimate is based on daps, which assesses the number of memory access operations (reads and writes) per second. Similar to flops, this tool is used to evaluate memory access performance, rather than locality. But it is still a good source of information, particularly in combination with the next estimate – cvg.
Fig.9 shows daps values for implementations of common algorithms, sorted in ascending order (the higher the daps, the better the performance in general). One can see, that the performance is good. The daps value is close to the Linpack test. It seems, that low temporal locality is compensated by spatial locality.
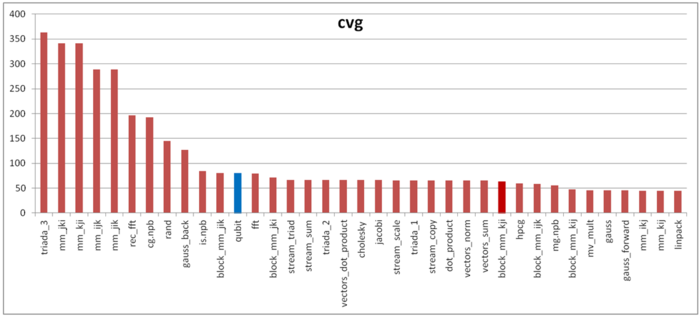
The second tool – cvg – is intended to obtain a more machine-independent locality assessment. It determines how often a program needs to pull data to cache memory. Respectively, the smaller the cvg value, the less frequently data needs to be called to cache, and the better the locality.
Fig.10 shows cvg values for the same set of implementations sorted in descending order (the smaller the cvg, the higher the locality in general). As we can see, the cvg is not so gooв as daps, and it's noticeably higher than for the Linpack test.
One of the possible explanations is an effect of arithmetic operations. There is a chance, that data is not read until the end of the arithmetic operations, this leads to the memory system dead time. Consequently, daps value for the program without arithmetic operations is lower, whenever cvg remains constant, and considered algorithm has very low amount of arithmetic operations.
As shown above, the locality depends on the parameter q (the index of affected qubit). So, it's important to analyze the daps and cvg values with respect to q. Both values were calculated for n=24 and all possible q values. Daps value remains constant (possibly, because of the small amount of arithmetic operations). Cvg changes on some critical value of q (is 80 for q < 15 and 55 for q > 15). It seems, that this change is due to the gap between fetched data in the third fragment, that was described in structure of memory access.