Thomas, locality

Primary author of this description: A.V.Frolov, Vad.V.Voevodin (Section 2), Alexey Teplov (Sections 3.

1 Links

The basic fragment of the implementation used for obtaining quantitative estimates is given here (Kernel function).

2 Locality of data and computations

One can see from the algorithm graph that the spatial locality of the data is fair. Indeed, all the arguments needed for an operation are calculated "nearby." However, the temporal locality is not as good. Suppose that the cache cannot hold all the problem data. Then repeated cache misses will occur while performing calculations in the upper left corner of a SLAE. Thus, one of the recommendations to application engineers using the elimination method is as follows: Arrange the calculations so that all the elimination paths are sufficiently short and their data can be placed in the cache.

The elimination method is an example of a serial algorithm with the locality of computations so high that it even becomes excessive . Computational cores of processors virtually cannot use their superscalar capabilities because the data needed by the basic operations of this method are produced by immediately preceding operations. This sharply deteriorates the performance of the elimination method even for modern single-processor and single-core systems.

2.1 Locality of implementation

2.1.1 Structure of memory access and a qualitative estimation of locality

Figure 1. Elimination method, pointwise version. The general memory access profile

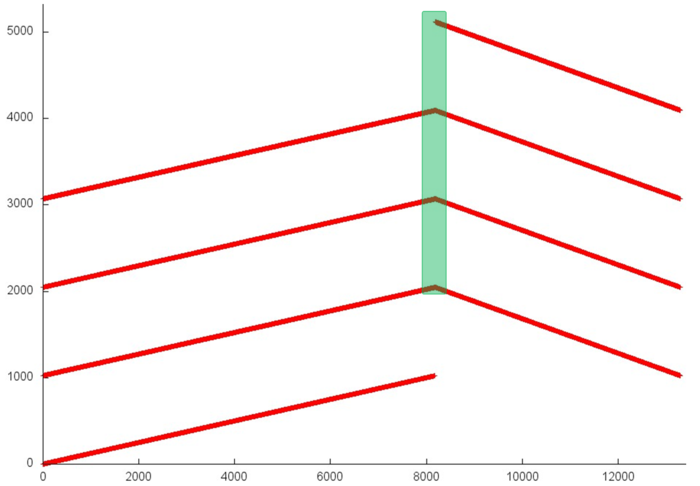
Figure 1 presents the memory access profile for an implementation of the pointwise version of elimination method. This profile is formed of accesses to 5 arrays storing three diagonals of the coefficient matrix, the vector of right-hand sides, and the resulting solution. Judging from the general profile, one can say that the subroutine is composed of two stages. At the first stage, it performs the serial access to entries of four arrays. The second stage is also the serial access performed in the reverse order.

Figure 2. An isolated fragment of the general profile (set out in green in fig. 1)

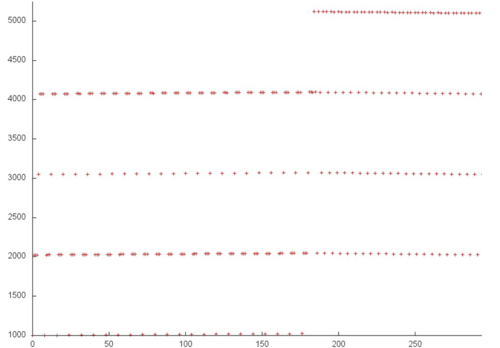
However, a closer look shows that the structure of the profile is somewhat more complicated (see fig. 2). At each step, some of the arrays are accessed several times to very close locations, which improves both spatial and temporal locality. Thus, the general profile has a high spatial locality (because serial accesses of the entries dominate here) and a medium temporal locality (because certain entries are immediately used again).

2.1.2 Quantitative estimation of locality

The start-up parameters are described here.

The first estimate is produced on the basis of daps, which estimates the number of memory accesses (reading and writing) per second. This characteristic, used for the interaction with memory, is an analog of the flops estimate. It largely estimates the performance of this interaction rather than locality. Nevertheless, this characteristic (in particular, its comparison with the next characteristic cvg) is a good source of information.

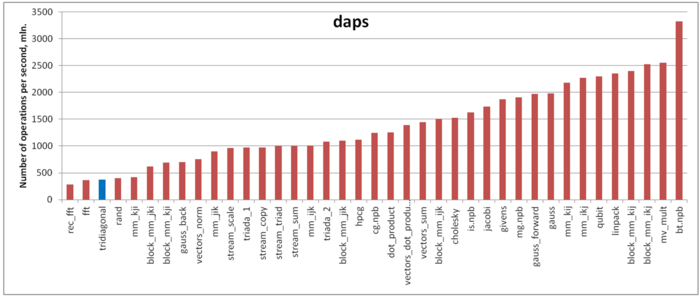
Figure 3 presents the values of daps for implementations of popular algorithms. They are arranged in increasing order (in general, the larger daps, the higher efficiency). The daps value of the subroutine under discussion is fairly unexpected. According to the above qualitative analysis, the locality of memory access is sufficiently high for this subroutine. However, daps estimates the performance of memory interaction to be worse than for the RandomAccess test! Such a distinction between locality and performance occurs not very often.

A detailed inspection of the original code reveals two reasons of this phenomenon. First of all, the iterations of the main loop are memory interdependent; that is, each iteration uses the data calculated by the preceding iteration. In this case, such an interdependence seems to significantly deteriorate the performance of memory interaction; on the other hand, it is rather good from the viewpoint of locality.

The second discovery is that, unexpectedly, one of divisions considerably slows down the execution of the subroutine. After this division was replaced by multiplication, the execution time reduced by a factor of 2.5. The assembler codes of two versions looked identical (except for the obvious replacement of a single division by multiplication). These features of the subroutine are not reflected in its locality properties, which resulted in such a substantial gap between the locality estimate and the performance of memory interaction.

Figure 3. Comparison of the values of daps

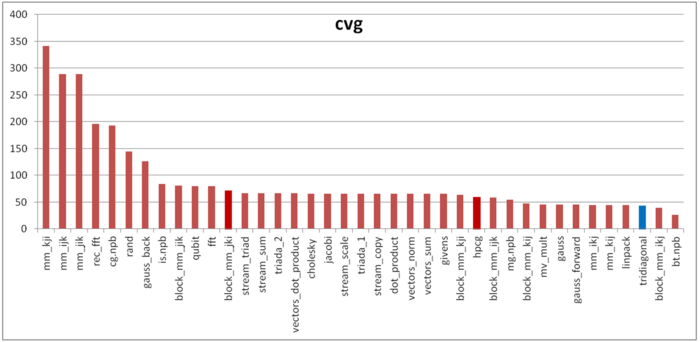
The second characteristic, called cvg, is intended for obtaining a locality estimate that would be more machine independent. It determines how often a program needs to fetch data to the cache memory. Accordingly, smaller values of cvg correspond to less often fetch operations and better locality.

Figure 4 presents the values of cvg for the same set of implementations. They are arranged in decreasing order (in general, the smaller cvg, the higher locality). Here, all our previous conclusions are confirmed by cvg: Locality turns out to be fairly good, which was already noted when discussing the qualitative locality estimate.

Figure 4. Comparison of the values of cvg

3 Scalability of the algorithm and its implementations

3.1 Scalability of the algorithm

There is no sense in discussing the scalability of the elimination method because it is completely non-parallel. However, we note that, for its parallel variants, the scalability should be analyzed in comparison with a single processor implementation of the classical method rather than with single processor implementations of these parallel variants.

An analysis of scalability was performed for the algorithm implemented in accordance with the methodology proposed in http://algowiki-project.org/ru/Scalability_methodology. The analysis was based on the experiments conducted on the Lomonosov supercomputer of the Moscow University Supercomputing Center].

3.2 Scalability of of the algorithm implementation

The variable start-up parameters of this implementation and their ranges are as follows:

• the number of processors is 1;
• the domain size varies in the range [10240 : 1024000] with the step 10240.

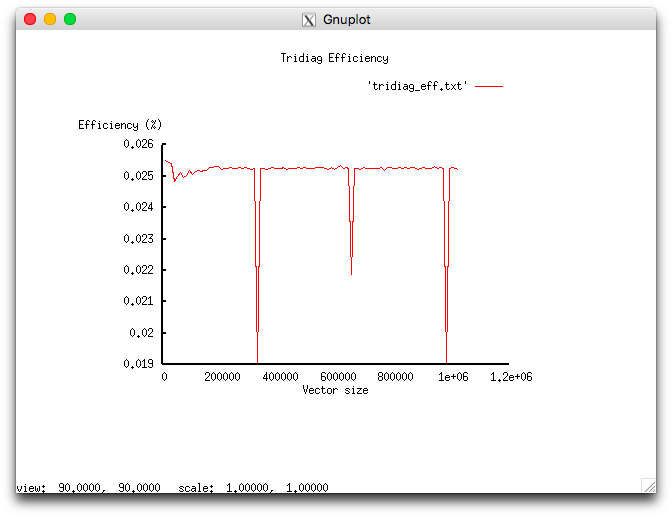
The experiments resulted in the following range for the efficiency of this implementation:

• the minimum efficiency is 0.019%;
• the maximum efficiency is 0.0255%.

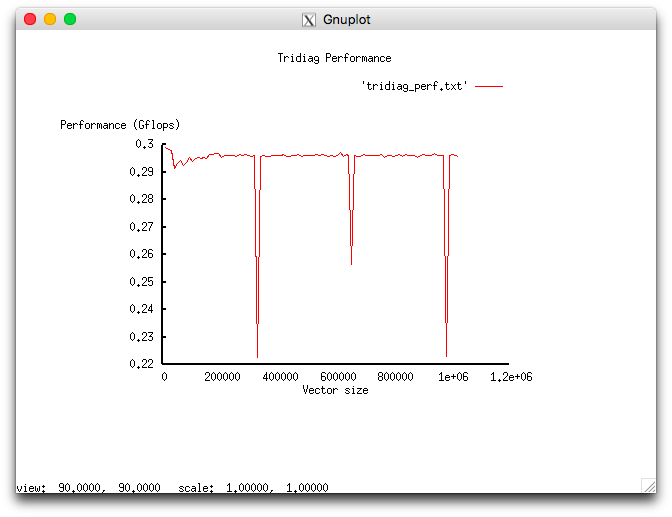
The following two figures show how the performance and efficiency of this implementation depend on the variable start-up parameters.

Figure 5. Implementation of the algorithm. Performance as a function of the vector size

Figure 6. Implementation of the algorithm. Efficiency as a function of the vector size

The low efficiency is likely to be related to the excessive locality discussed in the section on the locality of data and calculations.

4 Dynamic characteristics and efficiency of the algorithm implementation

In view of the serial nature of the algorithm and its excessive locality, the analysis of its dynamic characteristics seems to be of little value; therefore, it was not conducted.