Thomas algorithm, pointwise version

Thomas algorithm, pointwise version
Sequential algorithm
Serial complexity	[math]8n-7[/math]
Input data	[math]4n-2[/math]
Output data	[math]n[/math]
Parallel algorithm
Parallel form height	[math]5n-4[/math]
Parallel form width	[math]2[/math]

Primary authors of this description: A.V.Frolov.

1 Properties and structure of the algorithm

1.1 General description of the algorithm

Thomas algorithm is a variant of Gaussian elimination used for solving a system of linear algebraic equations (SLAE) [math]Ax = b[/math], where

[math] A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}, b = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix} [/math]

However, presentations of the elimination method often use a different notation and a numbering for the right-hand side and matrix of the system. For instance, the above SLAE can be written as

[math] A = \begin{bmatrix} c_{0} & -b_{0} & 0 & \cdots & \cdots & 0 \\ -a_{1} & c_{1} & -b_{1} & \cdots & \cdots & 0 \\ 0 & -a_{2} & c_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -a_{N-1} & c_{N-1} & -b_{N-1} \\ 0 & \cdots & \cdots & 0 & -a_{N} & c_{N} \\ \end{bmatrix}\begin{bmatrix} y_{0} \\ y_{1} \\ \vdots \\ y_{N} \\ \end{bmatrix} = \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots \\ f_{N} \\ \end{bmatrix} [/math]

(here, N=n-1). If each equation is written separately, then we have

[math]c_{0} y_{0} - b_{0} y_{1} = f_{0}[/math],

[math]-a_{i} y_{i-1} + c_{i} y_{i} - b_{i} y_{i+1} = f_{i}, 1 \le i \le N-1[/math],

[math]-a_{N} y_{N-1} + c_{N} y_{N} = f_{N}[/math].

Here, we examine the so-called right-elimination, which is the variant of elimination method in which a SLAE is processed top-down and then in the reverse direction. In this variant, one first goes top down eliminating the subdiagonal unknowns and then bottom up eliminating the superdiagonal ones. There is also a variant, called the left-elimination, in which a SLAE is first processed bottom-up and then top-down. There is basically no difference between both variants; consequently, we do not include a separate description of the left-elimination.

Figure 1. Graph of the elimination method for n=8. The input and output data are not shown. The symbols / and f denote division and operation a+bc or a-bc, respectively

1.2 Mathematical description of the algorithm

In the notation introduced above, the forward elimination path consists in calculating the elimination coefficients

[math]\alpha_{1} = b_{0}/c_{0}[/math],

[math]\beta_{1} = f_{0}/c_{0}[/math],

[math]\alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i})[/math], [math]\quad i = 1, 2, \cdots , N-1[/math],

[math]\beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i})[/math], [math]\quad i = 1, 2, \cdots , N[/math].

Then, in the backward elimination path, one calculates the solution

[math]y_{N} = \beta_{N+1}[/math],

[math]y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}[/math], [math]\quad i = N-1, N-2, \cdots , 1, 0[/math].

According to the literature (see ), these formulas are equivalent to calculating a variant of the [math]LU[/math] decomposition for the coefficient matrix accompanied by solving bidiagonal systems via forward and back substitutions.

1.3 Computational kernel of the algorithm

The computational kernel of this algorithm can be thought of as compiled of two parts, namely, the forward and backward elimination paths. The computational kernel of the forward elimination path consists of sequences of divisions, multiplications, and additions/subtractions. The computational kernel of the backward elimination path contains only multiplications and additions sequences.

Figure 2. Detailed graph of the elimination method for n=8 (each reciprocal number is only once calculated). The input and output data are not shown. Each calculation of a reciprocal number is marked by inv, and each multiplication is marked by mult. The operations repeated after the replacement of the right-hand side of SLAE are set out in grey

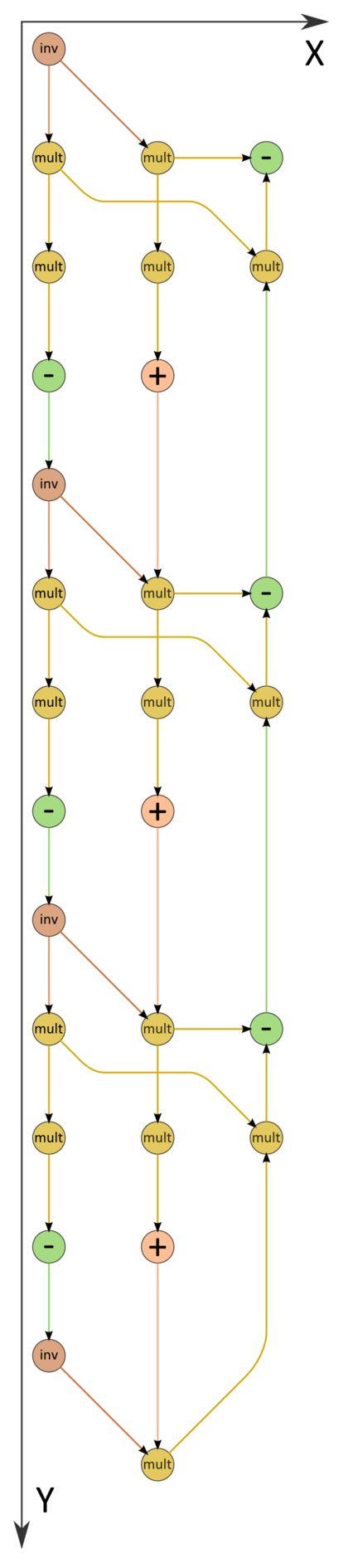
1.4 Macro structure of the algorithm

The macro structure of this algorithm can be represented as the combination of the forward and backward elimination paths. In addition, the forward path can also be split into two macro units, namely, the triangular decomposition of the coefficient matrix and the forward substitution for a bidiagonal SLAE. These units are executed simultaneously, that is, in parallel. The process of solving the bidiagonal SLAE uses the results produced by the triangular decomposition.

1.5 Implementation scheme of the serial algorithm

The method is executed as the following sequence of steps:

1. Initialize the forward elimination path:

[math]\alpha_{1} = b_{0}/c_{0}[/math],

[math]\beta_{1} = f_{0}/c_{0}[/math]

2. For [math]i[/math] increasing from [math]1[/math] to [math]N-1[/math], execute the forward path formulas:

[math]\alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i})[/math],

[math]\beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i})[/math].

3. Initialize the backward elimination path:

[math]y_{N} = (f_{N}+a_{N}\beta_{N})/(c_{N}-a_{N}\alpha_{N})[/math]

4. For [math]i[/math] decreasing from [math]N-1[/math] to [math]0[/math], execute the backward path formulas: [math]y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}[/math].

The formulas of the forward path contain double divisions by the same expressions. These divisions can be replaced by the calculation of reciprocal numbers succeeded by the multiplication by these numbers.

1.6 Serial complexity of the algorithm

Consider a tridiagonal SLAE consisting of [math]n[/math] equations with [math]n[/math] unknowns. The elimination method as applied to solving such a SLAE in its (fastest) serial form requires

• [math]2n-1[/math] divisions,
• [math]3n-3[/math] additions/subtractions, and
• [math]3n-3[/math] multiplications.

Thus, in terms of serial complexity, the elimination method is qualified as a linear complexity algorithm.

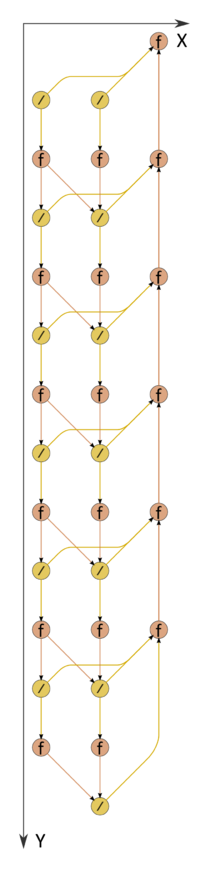
1.7 Information graph

The information graph of the elimination method is shown in fig. 1. An analysis indicates that this graph is virtually serial. During the forward path, two branches (namely, the left branch, corresponding to the matrix decomposition, and the central branch, responsible for the solution of the first bidiagonal system) can be executed in parallel. The right branch corresponds to the backward path. It is evident from the figure that not only the mathematical content of this process but also the structure of the algorithm graph and the direction of the corresponding data flows are in complete agreement with the appellation "backward path." The variant with divisions replaced by reciprocal number calculations is illustrated by the graph in fig. 2.

1.8 Parallelization resource of the algorithm

The parallel version of the elimination method as applied to solving a tridiagonal SLAE consisting of [math]n[/math] equations with [math]n[/math] unknowns requires that the following layers be executed:

• [math]n[/math] division layers (all the layers except for one contain [math]2[/math] divisions),
• [math]2n - 2[/math] multiplication layers and the same number of addition/subtraction layers ([math]n-1[/math] layers contain two operations of both types, while another [math]n-1[/math] layers contain a single operation of each type).

Thus, in terms of the parallel form height, the elimination method is qualified as an algorithm of complexity [math]O(n)[/math]. In terms of the parallel form width, its complexity is [math]2[/math].

1.9 Input and output data of the algorithm

Input data: tridiagonal matrix [math]A[/math] (with entries [math]a_{ij}[/math]), vector [math]b[/math] (with components [math]b_{i}[/math]).

Output data: vector [math]x[/math] (with components [math]x_{i}[/math]).

Size of the output data: [math]n[/math].

1.10 Properties of the algorithm

It is clearly seen that the ratio of the serial to parallel complexity is a constant (which is less than [math]2[/math]).

The computational power of the algorithm, understood as the ratio of the number of operations to the total size of the input and output data, is also a constant.

Within the framework of the chosen version, the algorithm is completely determined.

Routinely, the elimination method is used for solving SLAEs with diagonally dominant coefficient matrices. For such systems, the algorithm is guaranteed to be stable.

Suppose that several systems with the same coefficient matrix have to be solved. Then the left branch of calculations (see the figures with the algorithm graph) may not to be repeated. The reason is that the [math]LU[/math] decomposition of the coefficient matrix needs not to be recalculated. In such cases, the variant with divisions replaced by reciprocal number calculations is preferable.

2 Software implementation of the algorithm

2.1 Implementation peculiarities of the serial algorithm

Different implementations of the algorithm are possible depending on how the coefficient matrix is stored (as a single array with three rows or three distinct arrays) and how the calculated coefficients are stored (in locations of the already used matrix entries or separately).

Let us give an example of a Fortran subroutine implementing the elimination method. Here, all the matrix entries are stored in a single array; moreover, the entries neighboring in a row are located closely to each other, and the calculated coefficients are stored in locations of the original matrix entries.

      subroutine progm (a,x,N)
      real a(3,0:N), x(0:N)
      a(2,0)=1./a(2,0)
      a(3,0)=-a(3,0)*a(2,0) ! alpha 1
      x(0)=x(0)*a(2,0) ! beta 1
      do 10 i=1,N-1
        a(2,i)=1./(a(2,i)+a(1,i)*a(2,i-1))
        a(3,i)=-a(3,i)*a(2,i) ! alpha i+1
        x(i)=(x(i)-a(1,i)*x(i-1))*a(2,i) ! beta i+1
  10  continue
      a(2,N)=1./(a(2,N)+a(1,N)*a(2,N-1))
      x(N)=(x(N)-a(1,N)*x(N-1))*a(2,N) ! y N
      do 20 i=N-1,0,-1
        x(i)=a(3,i)*x(i+1)+x(i) ! y i
  20  continue
      return
      end

There are many simple implementations of the method on the web; see, for instance, Wikibooks - Algorithm implementation - Linear Algebra - Tridiagonal matrix algorithm.

2.2 Possible methods and considerations for parallel implementation of the algorithm

As seen from the analysis of the algorithm graph, it virtually cannot be parallelized (if not substantially modified). Consequently, there are two ways of adapting eliminations for parallel computers. If a problem uses eliminations, then the first way is to split it so as to obtain fairly many of them and assign a separate processor (separate core) to each elimination. The second way is to replace the elimination method by its parallel variants (the cyclic reduction method, serial-parallel variants, etc.).

The elimination method is present in all the standard program packages for linear algebra problems. However, it is so simple that most of the users (researchers and application engineers) prefer to write their own program segments implementing this method. It should be noted, though, that the elimination method in the standard packages is ordinarily not implemented in its pure form but rather as the pair "factorization into the product of two bidiagonal matrices" and "solution of a SLAE with the already factorized tridiagonal coefficient matrix." This is, for instance, the case with the SCALAPACK package and its predecessors.

2.4 Conclusions for different classes of computer architecture

The elimination method is intended for the classical von Neumann architecture. It is not even suitable for the effective loading of single core systems supporting superscalarity. In order to parallelize the process of solving a SLAE with a tridiagonal coefficient matrix, one should use some parallel substitute of this method, for instance, the most popular cyclic reduction or the new serial-parallel version of the elimination method. The latter yields to the former in terms of the critical path of the graph, but, instead, its graph has a more regular structure.