Участник:Дарья Соболева
Дарья Соболева: Многоклассовая логистическая регрессия
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Логистическая регрессия (Logistic regression) -- метод построения линейного классификатора, позволяющий оценивать апостериорные вероятности принадлежности объектов классам. Многоклассовая логистическая регрессия (Multiclass Logistic regression) -- логистическая регрессия, реализованная по схеме один против всех (one-vs-rest). При таком подходе строится столько моделей логистической регрессии, сколько классов необходимо обучить.
На вход алгоритму логистической регрессии подается матрица обЪектов-признаков [math]X[/math] и вектор допустимых ответов [math]Y[/math]. Предполагается, что существует целевая функция [math]y∗ : X → Y[/math]. Задача логистической регрессии как метода машинного обучения заключается в том, чтобы по выборке [math]X[/math] построить решающую функцию [math]a: X → Y[/math], которая приближала бы целевую функцию [math]y∗[/math].
Многоклассовая логистическая регрессия вместо вектора допустимых ответов [math]Y[/math] принимает список из векторов ответов для каждой задачи классификаци. Далее для каждого класса строится решающая функция.
1.2 Математическое описание алгоритма
Вход: обучающая выборка пар «объект, ответ» [math]X^l = \{(x_1,y_1),\dots,(x_l,y_l)\}[/math].
Случай двух классов
Положим [math]Y=\{-1,+1\}[/math]. Строится линейный алгоритм классификации [math]a: X\to Y[/math] вида [math]a(x,w) = \mathrm{sign}\left( \sum_{j=1}^D w_j f_j(x) + w_0 \right) = \mathrm{sign}\langle x,w \rangle[/math], где [math]w_j[/math] — вес [math]j[/math]-го признака, [math]w_0[/math] — порог принятия решения, [math]w=(w_0,w_1,\ldots,w_D)[/math] — вектор весов, [math]\langle x,w \rangle [/math]— скалярное произведение признакового описания объекта на вектор весов. Предполагается, что искусственно введён «константный» нулевой признак: [math]f_{0}(x)=1[/math]. Задача обучения линейного классификатора заключается в том, чтобы по выборке [math]X^l[/math] настроить вектор весов [math]w[/math]. В логистической регрессии для этого решается задача минимизации эмпирического риска с функцией потерь специального вида: [math]Q(w) = \sum_{i=1}^L \ln\left( 1 + \exp( -y_i \langle x_i,w \rangle ) \right) \to \min_{w}[/math]. После того, как решение [math]w[/math] найдено, становится возможным не только вычислять классификацию [math]a(x) = \mathrm{sign}\langle x,w \rangle[/math] для произвольного объекта [math]x[/math], но и оценивать апостериорные вероятности его принадлежности классам: [math]\mathbb{P}\{y|x\} = \sigma\left( y \langle x,w \rangle\right),\;\;y\in Y[/math], где [math]\sigma(z) = \frac1{1+e^{-z}}[/math] — сигмоидная функция.
Рассматриваемый в данной статье one-vs-rest подход позволяет легко свести задачу многоклассовой классификации к двум классам, так как предполагает построение двухклассовой логистической регрессии для каждого класса в отдельности. Метки [math]+1[/math] проставляются всем обЪектам рассматриваемого класса, а [math]-1[/math] проставляются обЪектам всех остальных классов. Для тестового объекта вычисляются предсказания всех обученных классификаторов, в качестве предсказания берется класс, с максимальной вероятностью.
1.3 Вычислительное ядро алгоритма
Вычислительным ядром многоклассовой логистической регрессии является число классов (параметр [math]M[/math]). Когда многоклассовая логистическая регрессия становится по сложности константой относительно количества классов, возникает уникальная возможность построения большого количества классификаторов одновременно.
1.4 Макроструктура алгоритма
Алгоритм многоклассовой логистической регрессии состоит в проведении следующих макроопераций:
- Для каждого объекта вычисление предсказаний (вероятностей наличия метки) для каждого класса [math]M[/math]
- Среди всех классов [math]M[/math] выбор того класса, вероятность которого оказалась максимальной
1.5 Схема реализации последовательного алгоритма
Формулы метода описаны выше. В последовательной реализации алгоритма сначала производится загрузка обучающей выборки. Далее создается массив весов при признаках модели, который инициализируются нулями. Затем для каждого класса производится обучение массива весов. Процесс обучения является итерационным. На каждой итерации для каждого объекта вычисляется предсказание модели. Затем вычисляется антиградиент минимизируемого функционала [math]Q(w)[/math] и производится сдвиг вектора весов на антиградиент, умноженный на скорость обучения. Число итераций и скорость обучения подбираются на основании обучающей выборки и сходимость модели. Я зафиксировала скорость обучения, равной [math]0.001[/math], а количество итераций, равным [math]10000[/math]. Это позволило мне получать точные и стабильные решения.
1.6 Последовательная сложность алгоритма
Обучение логистической регрессии в последовательном варианте имеет сложность [math] M * N * D * N_{iter} [/math], где [math]N_{iter}[/math] -- число итераций обучения алгоритма.
1.7 Информационный граф
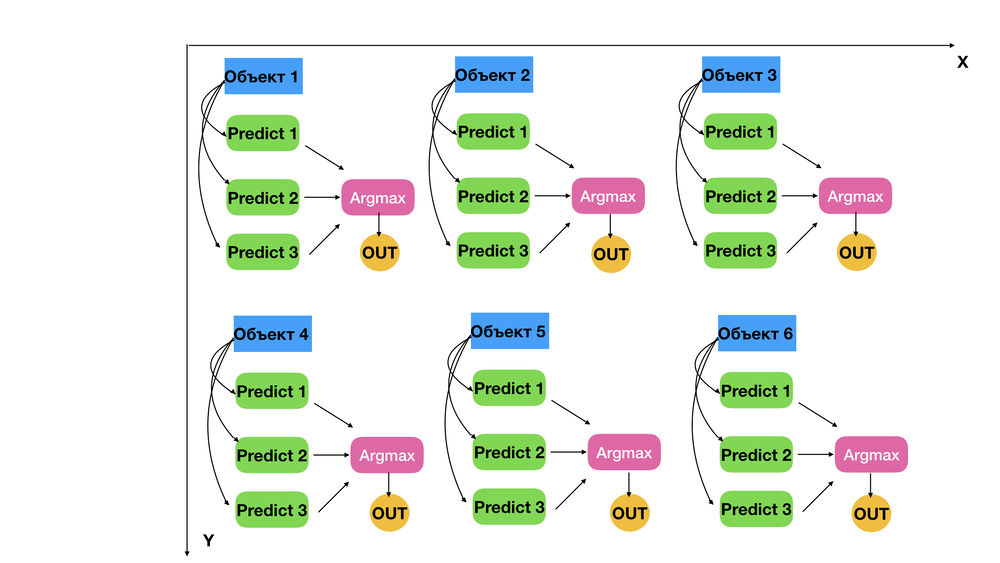
На рисунке 1 изображён граф алгоритма для случая [math]M = 3, N = 6[/math]. Синие вершины соответствуют объектам из обучающей выборки ([math]N[/math] объектов). Зеленые вершины соответствуют двухклассовым классификаторам ([math]M[/math] ветвей длины [math]1[/math]). Таким образом каждая логистическая регрессия строится независимо в отдельной ветви. Затем в розовых вершинах для каждого объекта вычисляется метка класса с наибольшей вероятностью. Итоговое предсказание заносится в желтую вершину.
1.8 Ресурс параллелизма алгоритма
Для алгоритма многоклассовой логистической регрессии в параллельном варианте требуется выполнить [math]N * D * N_{iter}[/math] шагов. [math]N_{iter}[/math] -- число итераций. Таким образом алгоритм является константным по количеству классов.
1.9 Входные и выходные данные алгоритма
Входные данные: обучающая выборка пар «объект, ответ» [math]X^l = \{(x_1,y_1),\dots,(x_l,y_l)\}[/math].
Дополнительные ограничения: отсутствуют.
Объём входных данных: N * D.
Выходные данные: Предсказания модели для каждого объекта.
Объём выходных данных: N.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
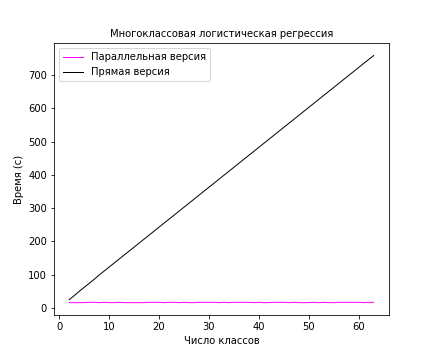
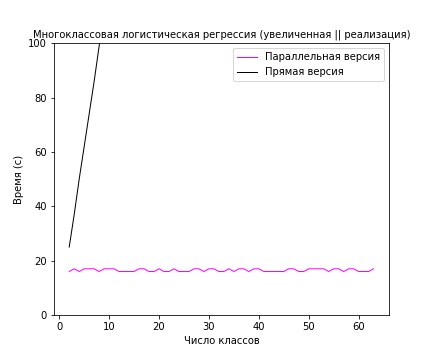
Для запуска прямой и параллельной версии алгоритма многоклассовой логистической регрессии был сгенерирован синтетический датасет, состоящий из [math]1000[/math] ([math]N = 1000[/math]) объектов с [math]500[/math] признаками ([math]D = 500 [/math]). Как видно на рисунке 2 параллельная версия показывает константное время работы от числа классов. В то время как последовательная версия уже линейно зависит от числа классов. Результаты были получены усреднением по [math]5[/math] запускам.
Все запуски производились на суперкомпьютере <<Ломоносов>>. В расчетах использовался процессор Intel Xeon X5570 с частотой [math]2.93[/math] GHz, кэшем [math]8192[/math] KB и [math]4[/math] ядрами. Эксперименты производились в очереди test, в которой доступно [math]16[/math] таких процессоров. Максимальное количество доступных мне ядер в очереди test составляло [math]16 * 6 = 64[/math]. В моих экспериментах число ядер было равно числу классов ([math]M[/math]).
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существует масса различных реализаций логистической регрессии на языке python. Приведу пример параллельной реализация из библиотеки sklearn -- Sklearn. Библиотека является открытой и достаточно популярной. Также стоит отметить реализацию параллельной логистической регрессии на программном каркасе PySpark -- PySpark. Код этой реализации также является открытым и активно используемым в задачах Big Data.