Участник:Руфина Третьякова/Хранение ненулевых элементов разреженных матриц. Умножение разреженной матрицы на вектор

Умножение разреженной матрицы на вектор
Последовательный алгоритм
Последовательная сложность	[math]nnz[/math]
Объём входных данных	[math]2(nnz+n)+1[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(n)[/math]
Ширина ярусно-параллельной формы	[math]O(n)[/math]

Авторы статьи: Третьякова Р. М. (группа 603), Буторина Е. В. (группа 603)

Руфина Третьякова отвечает за программную реализацию алгоритма, Екатерина Буторина - за написание статьи.

1 ЧАСТЬ. Свойства и структура алгоритма

1.1 Общее описание алгоритма

Разрежённая матрица — это матрица с преимущественно нулевыми элементами. В противном случае, если бо́льшая часть элементов матрицы ненулевые, матрица считается плотной. Среди специалистов нет единства в определении того, какое именно количество ненулевых элементов делает матрицу разрежённой. Разные авторы предлагают различные варианты. Разрежённые матрицы часто возникают при решении таких задач, как численное решение дифференциальных уравнений или уравнений в частных производных, а также при работе с графами. При хранении и преобразовании разрежённых матриц в компьютере бывает полезно, а часто и необходимо, использовать специальные алгоритмы и структуры данных, которые учитывают разрежённую структуру матрицы. Операции и алгоритмы, применяемые для работы с обычными, плотными матрицами, применительно к большим разрежённым матрицам работают относительно медленно и требуют значительных объёмов памяти. Однако разрежённые матрицы могут быть легко сжаты путём записи только своих ненулевых элементов, что снижает требования к компьютерной памяти. Сложность операции с разреженными матрицами чаще всего определяется не их размером но числом ненулевых элементов. Далее будет показано, что умножение разреженной матрицы на плотный вектор можно произвести ровно за столько умножений сколько в матрице ненулевых элементов.

1.2 Математическое описание алгоритма

Исходные данные: разреженная матрица [math]M^{n*n}[/math] (число ненулевых элементов матрицы равно [math]nnz[/math]), вектор [math]x^n[/math]

Существуют различные способы хранения разреженных матриц. Самый простой - каждый ненулевой элемент хранится в виде тройки: строчный индекс, столбцовый индекс, значение элемента. Такой способ хранения позволяет использовать объем памити равный [math]3*nnz[/math]. Существуют более экономные форматы, например "Compressed Sparse Row" или "Compressed Sparse Column", хранящие элементы по строкам и столбцам. Данные форматы требуют [math]2*nnz + n[/math] памяти. Наиболее удобным форматом для вычисления произведения матрицы на вектор является "Compressed Sparse Row" или сокращенно CSR-формат. Почему он наиболее удобен станет понятно далее.

Рассмотрим CSR-представление разреженной матрицы: пусть число ненулевых элементов матрицы равно [math]nnz[/math] CSR-формат представляет матрицу [math]M[/math] в виде 3-х одномерных массивов:

массив [math]A[/math] размера [math]nnz[/math] содержит ненулевые значения матрицы, [math]JA[/math] размера [math]nnz[/math] - номера столбцов ненулевых элементов., [math]IA[/math] размера [math]n[/math]- содержит номер с которого начинается описание элементов строки в массивах [math]A[/math] и [math]JA[/math].

Этот формат позволяет производить перемножение матрицы [math]M[/math] на вектор [math]x[/math] за [math]O(nnz)[/math] умножений и сложений. Если при умножении плотной матрицы на вектор каждый элемент результата определяется по формуле [math]y_i = \sum_{k = 1}^{n} A_{ik} x_k[/math], то в случае разреженной матрицы достаточно выполнять умножения только для ненулевых элементов [math]A_ik[/math], которые хранятся в массиве [math]A[/math] в части соответствующей строке [math]i[/math] (элементы с индексами от [math]IA_i[/math] до [math]IA_{i+1}[/math]). Необходимо также знать на какой элемент вектора должен быть домножен данный ненулевой элемент массива, то есть нужен столбцовый индекс каждого элемента [math]A[/math]. Для этого используется массив [math]JA[/math]. Таким образом, каждый элемент итогового вектора определятся формулой

[math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]

Нетрудно заметить, что общее число операций умножения равно числу элементов [math]A[/math], то есть числу ненулевых элементов разреженной матрицы.

Например, это разреженная матрица с 4-мя ненулевыми элементами

[math]\begin{pmatrix} 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 1 \\ 0 & 0 & 3 & 0 \\ 0 & 4 & 0 & 0 \\ \end{pmatrix}[/math],

представляемая в формате CSR

   A  = [ 2 1 3 4 ]
   IA = [ 0 0 2 3 4 ]
   JA = [ 0 3 2 1 ]

домножим ее на вектор

   x  = [ 5 6 7 8 ]

получим

   y[0] = 0
   y[1] = a[0]*x[0] + a[1]*x[3] = 18
   y[2] = a[2]*x[2] = 21
   y[3] = a[3]*x[1] = 24 

Алгоритм умножения матрицы на вектор полностью детерминирован и не зависит от порядка хранения элементов принадлежащих одной строке, поскольку сложение ассоциативно.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является формула умножения разреженной матрицы на плотный вектор:

[math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]

для всех [math]i = 1,n[/math]

1.4 Макроструктура алгоритма

Псевдокод алгоритма:

 Входные данные:
   число строк матрицы n; 
   разреженная матрица M в формате CSR:
     строчные указатели IA,
     столбцовые указатели JA, 
     ненулевые элементы A;
   вектор x.
 Выходные данные: произведение матрицы на вектор y.
 read CSR n, IA, JA, A;
 read x
 for i = 1,n:
   for k = IA(i), IA(i+1)-1:
           y(i) += A(k)*x(JA(k));
 write y;

1.5 Схема реализации последовательного алгоритма

Метод можно описать следующим образом:

1. привести матрицу [math]M[/math] к формату CSR
2. для [math]i[/math] от [math]0[/math] до [math]n-1[/math] вычислить [math]y_i[/math] по формуле [math]y_i = \sum_{k = IA_i}^{IA_{i+1}} A_k x_{JA_k}[/math]

1.6 Последовательная сложность алгоритма

Для вычисления матрично-векторного произведения матрицы размера [math]n*n[/math] и вектора размера n в последовательном варианте требуется:

• [math]nnz - 1[/math] сложений,
• [math]nnz[/math] умножений.

1.7 Информационный граф

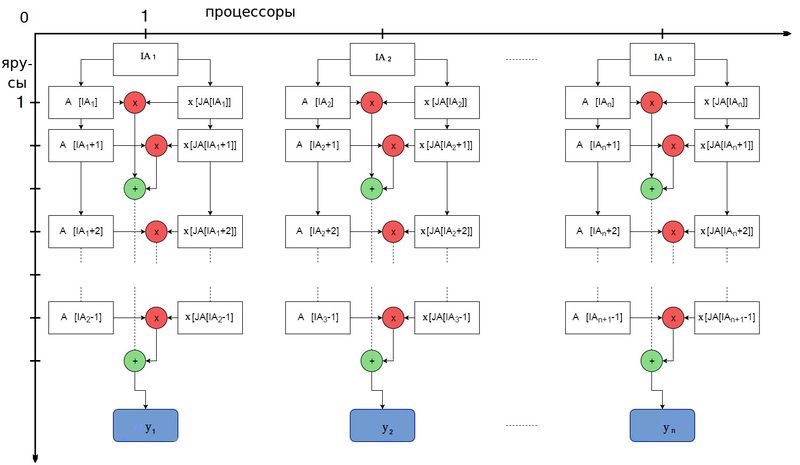
Для того чтобы построить информационный граф рассмотрим процесс вычисления значения одного элемента результирующего вектора [math]y_i[/math]. Число последовательных ярусов равно числу последовательных операций -- [math] AI_{i+1} - AI_i [/math] (в данном случае умножение и сложение будем считать за одну операцию). Если же вычисления всех [math]y_i[/math] производить параллельно, на каждом ярусе будет производиться [math]n[/math] операций.

Информационный граф алгоритма умножения разреженной матрицы на плотный вектор (Рисунок составлен самостоятельно)

1.8 Ресурс параллелизма алгоритма

Возможность параллельной реализации алгоритма появляется благодаря независимости вычисления каждого элемента результирующего вектора [math]y_i[/math]. Предположим, что имеется неограниченное число процессоров (теоретически, для максимальной эффективности требуется [math]n[/math] процессоров). Каждый процессор работает с одной строкой разреженной матрицы и хранит в памяти только те части массивов [math] AJ [/math] и [math] A [/math], которые соответствуют данной строке. Вектор [math] x [/math] хранится в памяти всех процессоров. Таким образом достигается экономия памяти (объем данных для i-ого процессора [math] 2(AI_{i+1} - AI_i) + n [/math]). На данном процессоре выполняется [math] AI_{i+1} - AI_i [/math] последовательных операций умножения и сложения. Число ярусов для i-ого процессора равно [math] AI_{i+1} - AI_i [/math]. Поскольку изначальная разреженная матрица имеет произвольную структуру, число ярусов на различных процессорах может быть различно. В худшем случае (если в строке все элементы ненулевые) число ярусов будет равно [math]n[/math].

Таким образом, для алгоритма умножения разреженной матрицы на плотный вектор в параллельном варианте требуется последовательно выполнить:

• не более чем [math]n[/math] ярусов умножений и сложений,
• в каждом из ярусов не более чем [math]n[/math] операций.

При классификации по высоте ЯПФ, таким образом, алгоритм умножения матрицы на вектор относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет линейной.

Замечание1: если число процессоров [math]k[/math] меньше числа строк, но отношение [math]\frac{n}{k} = c[/math] является константой, то каждый процессор вычисляет [math]c[/math] элементов результирующего вектора, и число ярусов не более чем [math]cn[/math]. Таким образом, предыдущие оценки сложности сохранятся.

Замечание2: для данного формата хранения использование более чем [math]n[/math] процессоров не имеет смысла

1.9 Входные и выходные данные алгоритма

Входными данными алгоритма являются:

1. размер разреженной матрицы [math] n [/math];
2. вектор [math] AI [/math] размерности [math] n+1 [/math];
3. вектор [math] AJ [/math] размерности [math] nnz [/math];
4. вектор [math] A [/math] размерности [math] nnz [/math];
5. вектор [math] x [/math] размерности [math] n [/math].

Суммарная размерность входных данных: [math] 2(nnz + n) + 1 [/math]

Выходными данными является

1. вектор [math] y [/math] размерности [math] n [/math].

Объем выходных данных: [math] n [/math].

1.10 Свойства алгоритма

Если размерность матрицы [math]n[/math], число ненулевых элементов [math]nnz[/math], для вычисления используется [math]k[/math] процессоров тогда:

• Каждый процессор оперирует с [math]\frac{n}{k}[/math] строками, в каждой из которых примерно [math]\frac{nnz}{n}[/math] элементов. Параллельная сложность алгоритма - [math]O(\frac{nnz}{k})[/math].

• Вычислительная мощность алгоритма (отношение числа операций к суммарному объему входных и выходных данных) - [math]O(\frac{nnz}{2nnz + 3n}) = O(1)[/math] - для последовательного алгоритма; [math]O(\frac{nnz}{n} / (2\frac{nnz}{n} + n)) = O(1) [/math] - для параллельного алгоритма.

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Наитивная реализация алгоритма следующая:

1. один процессор назначается управляющим
2. управляющий процессор считывает или генерирует (если матрица задается известной формулой) матрицу в CSR формате [math] [ AI, AJ, A ] [/math]
3. управляющий процессор считывает или генерирует вектор [math] x [/math]
4. управляющий процессор разделяет матрицу на блоки в зависимости от числа процессоров и рассылает остальным процессорам строки матрицы и вектор
5. все процессоры вычисляют произведение своего блока матрицы на вектор
6. управляющий процессор собирает результаты

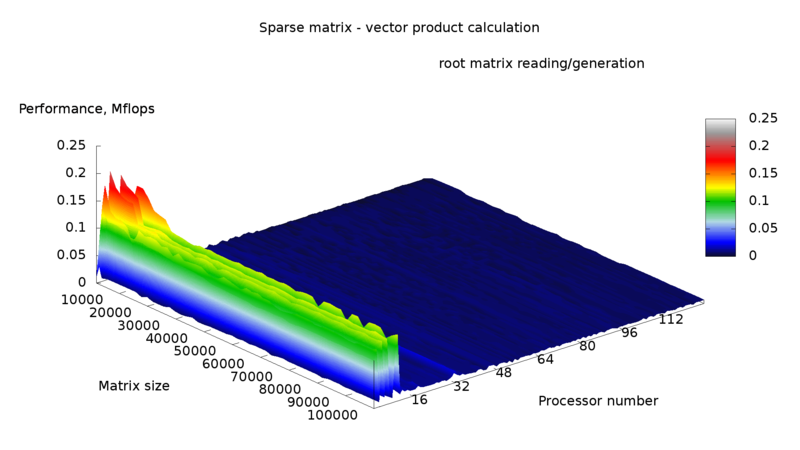
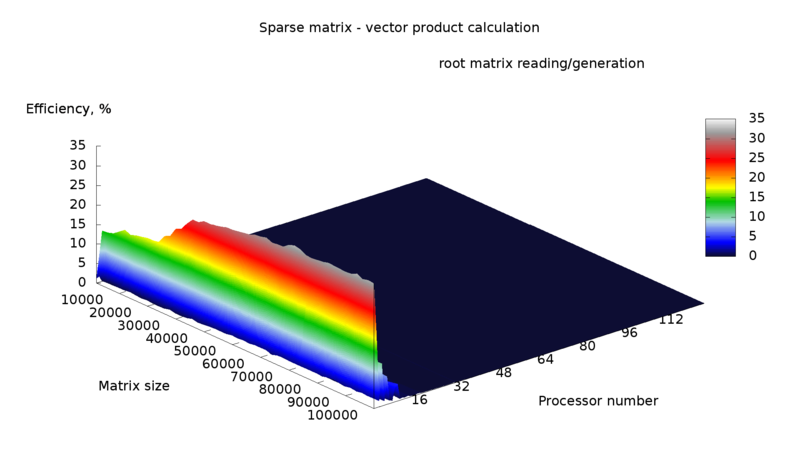
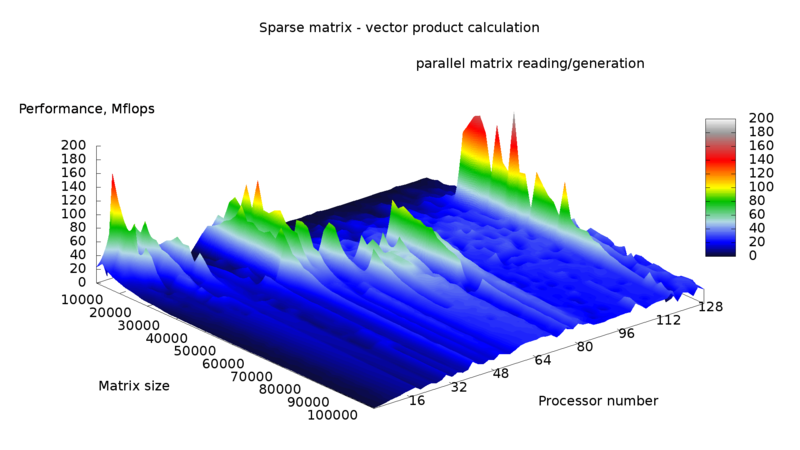
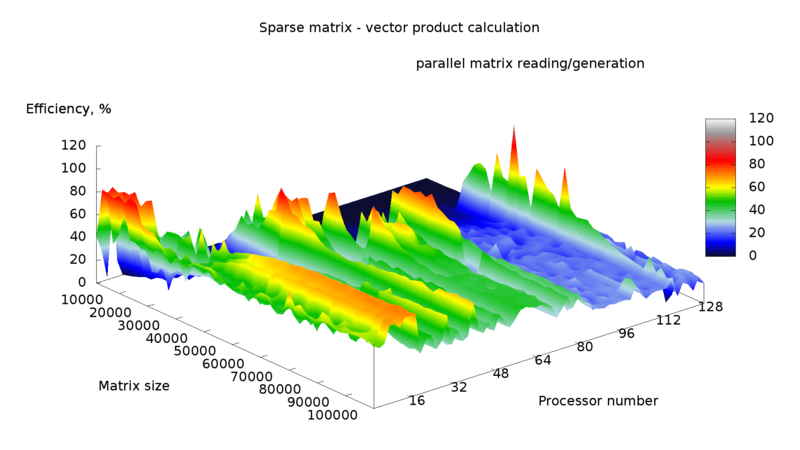
Данный алгоритм несмотря на кажущуюся простоту оказывается весьма неэффективен, так как время пересылок оказывается на порядки больше времени вычисления. Более того, при большом количестве процессоров время выполнения параллельной программы оказывается больше времени выполнения последовательной программы. Производительность и эффективность работы данного алгоритма показаны на рисунках 1 и 2.

• 

  Рисунок 1: производительность умножения разреженной матрицы на вектор при считывании управляющим процессором (время считывания и пересылок учтено)
• 

  Рисунок 2: эффективность умножения разреженной матрицы на вектор при считывании управляющим процессором (время считывания и пересылок учтено)

Проблема многих современных параллельных вычислительных систем заключается в том, что скорость обмена между процессорами существенно отстает от скорости произведения операций самими процессорами, а также число каналов связи много меньше числа процессоров, отчего возникают дополнительные задержки. Потому необходимо создавать алгоритмы которые по возможности будут использовать меньшее число операций пересылок данных.

Улучшенный алгоритм:

1. каждый процессор вычисляет блок матрицы (индексы строк) с которым ему предстоит работать в зависимости от своего порядкового номера
2. каждый процессор генерирует или считывает (при помощи процедур параллельного чтения) свой блок матрицы, и вектор
3. каждый процессор вычисляет произведение своего блока матрицы на вектор
4. управляющий (нулевой) процессор собирает результат или же каждый процессор записывает свою часть результата (при помощи процедур параллельной записи)

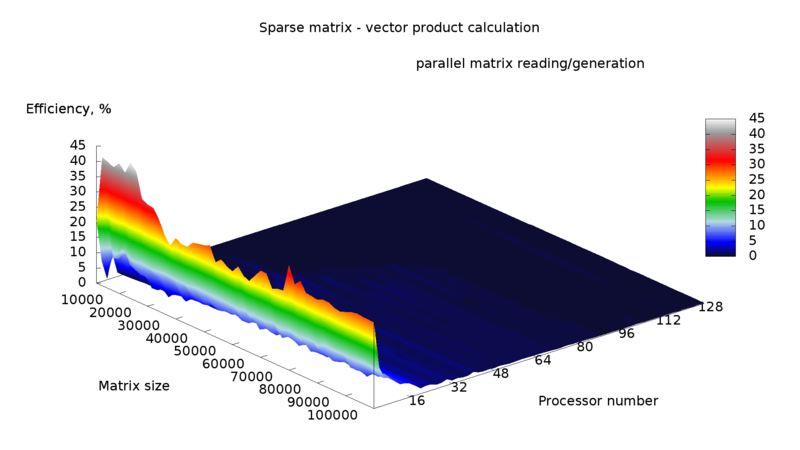
Данный алгоритм отличается лучшим быстродействием (по крайней мере, время работы параллельной программы уменьшается с увеличением числа процессоров). Производительность и эффективность алгоритма можно увидеть на рисунках 3-6.

• 

  Рисунок 3: производительность умножения разреженной матрицы на вектор при параллельном считывании (время считывания и пересылок учтено)
• 

  Рисунок 4: эффективность умножения разреженной матрицы на вектор при параллельном считывании (время считывания и пересылок учтено)

• 

  Рисунок 5: производительность умножения разреженной матрицы на вектор при параллельном считывании (учитывается только время вычислений)
• 

  Рисунок 6: эффективностьь умножения разреженной матрицы на вектор при параллельном считывании (учитывается только время вычислений)

Следует заметить, что в данной реализации матрица генерировалась при помощи случайных чисел, и кроме того кластер, на котором производились эксперименты не является однородным, различные ядра имеют различные характеристики, вследствие чего возникает "рельефность" производительности и эффективности.

Если производить анализ алгоритма по суммарному времени работы программы (рис. 3,4), то эффективность уменьшается практически до нуля при увеличении числа процессоров, а производительность выше при малом числе процессоров и малом размере матрицы, за исключением нескольких "пиков" на средних размерах матрицы и большом числе процессоров. Если же анализировать непосредственно время вычислений, то производительность и эффективность оказываются значительно выше. На "пиках" наблюдается сверхлинейное ускорение (рис. 6), и в целом эффективность лучше для больших размеров матрицы. Производительность также имеет данные "пики", и становится выше для больших размеров матрицы.

Тестирование производилось на кластере cluster2 ИВМ РАН. http://cluster2.inm.ras.ru/

2.7 Существующие реализации алгоритма

Последовательная реализация имеется в пакете SPARSKIT [1], Python.Scipy [2]

Параллельный алгоритм реализован в библиотеке Matlab [3], Intel MKL [4]

3 Литература

[1] С. Писсанецки. Технология разреженных матриц. Изд. Мир, 1988.

[2] В. В. Воеводин, Вл.В. Воеводин. Параллельные вычисления. – СПб.: БХВ - Петербург, 2002.