Участник:Alexeyshekhanov/Сортировка пузырьком
Сортировка пузырьком
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Сортировка пузырьком — это алгоритм сортировки, который последовательно проходит по списку, сравнивает пары соседних элементов и меняет их местами, если они стоят в неправильном порядке. Этот процесс продолжается до тех пор, пока весь список не будет отсортирован. Название "пузырьком" происходит от того, что наибольшие элементы "всплывают" к концу списка
1.2 Математическое описание алгоритма
Давайте представим список из n элементов, обозначим его как [math]A[0], A[1], ..., A[n-1][/math]. Сортировка пузырьком выполняет следующие шаги: 1. Начнем с индекса [math]i = 0[/math]. 2. Для каждого [math]i[/math] от [math]0[/math] до [math]n - 1[/math], сравниваем [math]A[i][/math] и [math]A[i+1][/math]. 3. Если [math]A[i] \gt A[i+1][/math], меняем их местами. 4. После первого прохода самый большой элемент окажется в конце списка. 5. Уменьшаем n на 1 и повторяем шаги 1 и 2 для оставшихся элементов. Продолжаем выполнять проходы до тех пор, пока список не станет отсортированным.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро последовательной версии сортировки пузырьком можно составить из, в худшем случае, [math]\frac{n (n - 1)}{2}[/math] сравнений и обменов.
1.4 Макроструктура алгоритма
Как и было сказано выше, основную часть метода занимают сравнения и перестановки. Дополнительные функции не использутся.
1.5 Схема реализации последовательного алгоритма
Реализация последовательного алгоритма на языке c++:
void bubbleSort(int arr[], int n)
{
int i, j;
for (i = 0; i < n - 1; i++)
for (j = 0; j < n - i - 1; j++)
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
1.6 Последовательная сложность алгоритма
Относится к алгоритмам с квадратичной сложностью - [math]\Theta(n^2)[/math]
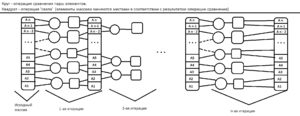
1.7 Информационный граф
Информационный граф состоит из [math]n[/math] итераций, где разбиение элементов на пары начинается с нулевого элемента на каждой четной начинается, а на каждой нечетной с первого. Каждую такую пару может обрабатывать отдельный поток, независимо от других.
Это можно увидеть на примере, который изображен на рис. 2. Красным обведены элементы, которые сравниваются и "обмениваются" на данной итерации.
1.8 Ресурс параллелизма алгоритма
Ресурсом параллелизма в данном алгоритме является возможность независимого выполнения операций сравнения двух соседних элементов и последующего обмена этих элементов. Эти вызовы обрабатывают разные части данных и не зависят друг от друга, что позволяет выполнять их одновременно на разных потоках.
В параллельной версии сортировки пузырьком мы каждую пару последовательно стоящих в массиве элементов подаем на отдельный поток. Это означает, что в идеальном случае (количество потоков неограниченно, затраты на создание потоков и синхронизацию между ними игнорируются) операции сравнения и замены индексов могут выполняться одновременно. Таким образом каждый шаг сортировки имеет временную сложность [math]\Theta(1)[/math], а максимальное время, необходимое для сортировки, будет n, соответственно временная сложность будет [math]\Theta(n)[/math].
Но на практике, когда ресурсы ограничены, получается, что при количестве потоков равном p, временная сложность становится [math]\Theta(\frac{n^2}{p})[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: Произвольный массив произвольного размера
Выходные данные: Тот же самый массив, но уже отсортированный
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Масштабируемость алгоритма сортировки пузырьком определяется размером входных данных и количеством доступных потоков. 1. В случае с входными данными, чем больше их размер, тем лучше масштабируемость. 2. В случае же с доступными потоками, то не всегда их число прямо пропорционально влияет на скорость выполнения сортировки. С какого то количества потоков, в зависимости от размера входных данных, сортировка начинает выполняться все медленнее и медленнее из за накладных расходов, таких как создание потоков, их синхронизация и т.п.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Посмотрим на некоторые существующие улучшения последовательной сортировки пузырьком.
1) Реализация с проверкой обмена.
void bubbleSort(int arr[], int n)
{
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++)
{
swapped = false;
for (j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
swap(arr[j], arr[j + 1]);
swapped = true;
}
}
if (swapped == false)
break;
}
}
В данной реализации прирост скорости выполнения происходит за счет введения переменной swapped, и проверки ее значения. Конечно не во всех ситуациях, но некоторых массивах данный вариант будет работать быстрее.
2) Четная - нечетная сортировка
void oddEvenBubbleSort(int *arr, int n, int threadsNumber)
{
int i, j;
for (i = 0; i < n; i++)
{
int first = i % 2;
for (j = first; j < n - 1; j+=2)
{
if (arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
}
Этот вариант сортировки на случайно заполненных массивах показывал лучшее время из вышеупомянутых. Но главное его преимущество в том, данный алгоритм удобнее всего распараллеливать.
3 Литература
- Левитин А. В. Глава 3. Метод грубой силы: Пузырьковая сортировка // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 144—146. — 576 с. — ISBN 978-5-8459-0987-9
- Абрамов С. А., Лекции о сложности алгоритмов. — М.: МЦНМО, 2009. - 256 с. - ISBN 978-5-94057-433-0