Участник:Anlesnichiy/Решение задачи Коши для системы ОДУ методом Рунге-Кутты 4 порядка

Эта работа прошла предварительную проверку Дата последней правки страницы: 22.11.2016 Данная работа соответствует формальным критериям. Проверено VadimVV.

Решение задачи Коши для системы ОДУ методом Рунге-Кутты 4 порядка
Последовательный алгоритм
Последовательная сложность	[math] 4mn [/math]
Объём входных данных	[math] m + 3 [/math]
Объём выходных данных	[math] (m+1)n [/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] O(n) [/math]
Ширина ярусно-параллельной формы	[math] O(m) [/math]

Основные авторы описания: А.А. Лесничий(1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9), Д.А. Алимов(1.1,1.7,1.10,2.4,2.7)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Рунге-Кутты четвертого порядка — наиболее распространенный метод из семейства методов Метод Рунге-Кутты численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Данные итеративные методы явного и неявного приближённого вычисления были разработаны около 1900 года немецкими математиками К. Рунге и М. В. Куттой.

Формально, методом Рунге-Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения.
Основная идея алгоритмов Рунге - Кутты состоит в замене правой части дифференциального уравнения, зависящей от искомой неизвестной функции, некоторым приближением. Если задачу Коши переписать в интегральном виде

[math] y(x) = y_{0} + \int\limits_{x_{0}}^{x}f(t,y)dt, [/math]

то, применяя различные численные формулы для расчёта интеграла в правой части уравнения, можно получить методы Рунге - Кутты различных порядков.

Общий вид формул методов Рунге - Кутты с шагом сетки [math]h_{n}[/math]:

[math] y = f(t,y),\,\,\, y(t_{0}) = y_{0}, [/math]

[math] y_{n+1} = y_{n} + h_{n+1}\sum\limits_{i=1}^{s}b_{i}K_{n}^{i}, [/math]

где

[math] K_{n}^{i} = f(t_{n} + c_{i}h_{n+1}, y_{n} + h_{n+1}\sum\limits_{j=1}^{i-1}a_{ij}K_{n}^{j}). [/math]

Конкретный метод Рунге - Кутты определяется набором коэффициентов [math]b_{i}, c_{j}, a_{ij}[/math], которые должны удовлетворять определённым соотношениям.

1.2 Математическое описание алгоритма

1.2.1 Метод Рунге-Кутты 4-го порядка для задачи Коши для ДУ первого порядка

Рассмотрим задачу Коши, где правая часть удовлетворяет условиям теорем существования и единственности решения.

[math] y' = f(x,y),\ a \leq x \leq b;\ y(a) = y^0 [/math]

Зададим равномерную сетку

[math] x_i = a + ih,\ i = 1,\dots, n,\ h = \frac{b-a}{n} [/math]

Введём обозначения [math]y(x_i) = y_i[/math]. Получим вычислительную формулу:

[math] \begin{cases} k_1 = hf(x_i,y_i)\\ k_2 = hf(x_i + h/2,y_i + k_1/2)\\ k_3 = hf(x_i + h/2,y_i + k_2/2)\\ k_4 = hf(x_i + h,y_i + k_3)\\ y_{i+1} = y_i + [ k_1 + 2k_2 + 2k_3 + k_4 ]/6 \\ \end{cases} [/math]

1.2.2 Метод Рунге-Кутты 4-го порядка для задачи Коши для системы ДУ первого порядка

Численное решение задачи Коши для систем ОДУ 1-го порядка методами Рунге-Кутты ищется по тем же формулам, что и для ОДУ первого порядка. Например, решение методом Рунге-Кутты 4-го порядка можно найти, если положить:

[math] y_i \rightarrow \bar y_i [/math]

[math] f(x_i,y_i) \rightarrow \bar f(x_i,\bar y_i) [/math]

[math] k_l \rightarrow \bar k_l [/math]

[math] \bar k_l = \begin{pmatrix} k^i_{l,1}\\ \vdots\\ k^i_{l,m}\\ \end{pmatrix} [/math]

где m – размерность системы, [math] l = 1, \dots, 4 [/math]. В результате получим

[math] \begin{cases} \bar k_1 = h\bar f(x_i,\bar y_i)\\ \bar k_2 = h\bar f(x_i + h/2,\bar y_i + \bar k_1/2)\\ \bar k_3 = h\bar f(x_i + h/2,\bar y_i + \bar k_2/2)\\ \bar k_4 = h\bar f(x_i + h,\bar y_i + \bar k_3)\\ \bar y_{i+1} = \bar y_i + [ \bar k_1 + 2\bar k_2 + 2\bar k_3 + \bar k_4 ]/6 \\ \end{cases} [/math]

1.3 Вычислительное ядро алгоритма

Вычислительным яром алгоритма можно считать вычисление значение вектора [math] \bar y_i [/math], то есть вычислительным ядром является цикл по i. Иными словами сам алгоритм совпадает со своим ядром и был описан в пункте 1.2.2.

1.4 Макроструктура алгоритма

Макроструктуру алгоритма составляют вычисления коэффициентов [math]k_{j},\,j=1,..,4[/math] при нахождении значений искомой функции в каждом узле.

1.5 Схема реализации последовательного алгоритма

Приведем возможную реализацию последовательного алгоритма на языке Matlab (правая часть ОДУ задана в виде функции func(x,y))

 1  function [x, y] = RungeKutta4(y0, a, b, n)
 2      h = (b-a)/n;
 3      x = a : h : b
 4 
 5      y(:, 1) = y0;
 6      for i = 2 : n
 7          k1        = h*func(x(i), y(:, i))
 8          k2        = h*func(x(i) + h/2, y(:, i) + k1/2)
 9          k3        = h*func(x(i) + h/2, y(:, i) + k2/2)
10          k4        = h*func(x(i) + h, y(:, i) + k3)
11          y(:, i+1) = y(:, i) + (k1 + 2*k2 + 2*k3 + k4)/6 
12      end
13  end

1.6 Последовательная сложность алгоритма

Каждый шаг цикла алгоритма состоит из 4 обращений к функции [math] \bar f [/math], 11 умножений и 10 сложений. Так как обращение к функции [math] \bar f [/math] является наиболее сложной операцией, то сложность линейного выполнения алгоритма можно определить как [math] 4mn [/math].

1.7 Информационный граф

Опишем граф алгоритма аналитически и графически.
Пусть задана система из [math] m [/math] одномерных дифференциальных уравнений. Граф имеет трёхмерную структуру, которая представляет собой связанные между собой ограниченные плоскости (уровни). На каждом i-ом уровне вычисляется i-ое приближение вектора решения системы. Всего таких уровней – n, где n – количество узлов, в которых вычисляется приближённое решение системы дифференциальных уравнений. Выходные данные i-го уровня являются входными данными для i+1-го уровня.
Вершины информационного графа делятся на два типа:

• Первому типу вершин соответствует вычисление одной координаты функции, стоящей в правой части дифференциального уравнения, в точках, подаваемых на вход вершине. Результатом выполнения операции является одна координата вектора [math]k_{l},\,\,\,l = 1,2,3,4[/math]. На каждом уровне таких вершин будет [math]4m[/math], а их общее количество – [math]4mn[/math].
• Второму типу вершин соответствует операция [math]a + bc[/math]. Эти вершины также можно разделить на две группы. В вершинах первой группы вычисляются выражения, результат которых будет подаваться в качестве аргументов для вершин первого типа, при этом входными данными для этих вершин будут результаты срабатывания m вершин первого типа, расположенных на одном уровне. На каждом уровне вершин первой группы будет [math]3m[/math], а их общее количество – [math]3mn[/math]. Входными данными для вершин второй группы будет результат срабатывания одной вершины первого типа и одной такой же вершины второго типа. Результатом срабатывания данной вершины на i-ом уровне будут m координат вектора i-го приближения решения системы. На каждом уровне таких вершин будет [math]4m[/math], а их общее количество – [math]4mn[/math].

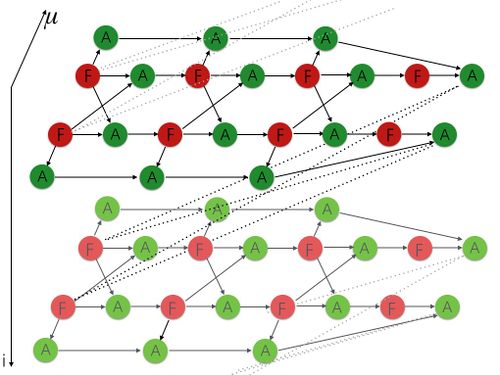
Приведём графическую иллюстрацию информационного графа (рис. 1). Для того чтобы сильно не загромождать граф, рассмотрим случай системы из двух дифференциальных уравнений. Красным цветом обозначены вершины первого типа, зелёным - вершины второго типа. Входные данные задачи подаются на все вершины первого типа, а также на [math]m[/math] левых вершин второй группы второго типа и на все вершины первой группы второго типа на первом уровне подаются начальные значения искомой функции (см. пункт 1.8). Выходными данными будут результаты срабатывания [math]m[/math] правых вершин второй группы второго типа на каждом уровне. Результаты срабатывания остальных вершин являются промежуточными данными алгоритма.

Рисунок 1. Информационный граф для системы из двух дифференциальных уравнений.

1.8 Ресурс параллелизма алгоритма

Поскольку в описанной выше вычислительной схеме наиболее трудоемкой является операция расчета правых частей ОДУ при вычислении [math]k_i ( i = 1, \dots, 4) [/math], то основное внимание следует уделить распараллеливанию этой операции. Здесь будет применяться подход декомпозиции уравнений системы ОДУ на подсистемы. Поэтому для инициализации рассмотрим следующую схему декомпозиции данных по имеющимся процессорным элементам с локальной памятью: на каждый [math]\mu[/math]- ПЭ (процессорный элемент) ([math]\mu = 0, \dots, p-1 [/math]) распределяется [math] n/p [/math] дифференциальных уравнений и вектор [math] \bar y_0 [/math]. Далее расчеты производятся по следующей схеме:

1. на каждом ПЭ одновременно вычисляются [math] n/p [/math] соответствующих компонент вектора [math] \bar k_1 [/math] по формуле [math] [ \bar k_1 ]_{\mu} = h[ \bar f(x_i, \bar y_i) ]_{\mu} [/math]
2. для обеспечения второго расчетного этапа необходимо провести сборку вектора [math] \bar k_1 [/math] целиком на каждом ПЭ. Затем независимо выполняется вычисление компонент вектора [math] \bar k_2 [/math] по формуле [math] [ \bar k_2 ]_{\mu} = h[ \bar f(x_i + h/2,\bar y_i + \bar k_1/2)]_{\mu} [/math];
3. проводится сборка вектора [math] \bar k_2 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_3:\ [ \bar k_3 ]_{\mu} = h [\bar f(x_i + h/2,\bar y_i + \bar k_2/2)]_{\mu} [/math];
4. проводится сборка вектора [math] \bar k_3 [/math] на каждом ПЭ, вычисляются компоненты вектора [math] \bar k_4:\ [ \bar k_4 ]_{\mu} = h [\bar f(x_i + h,\bar y_i + \bar k_3)]_{\mu} [/math];
5. рассчитываются с идеальным параллелизмом компоненты вектора [math] \bar y_{i+1}:\ [\bar y_{i+1}]_{\mu} = [\bar y_{i}]_{\mu} + ([ \bar k_1 ]_{\mu} + 2[ \bar k_2 ]_{\mu} + 2[ \bar k_3 ]_{\mu} + [ \bar k_4 ]_{\mu})/6\ [/math] и производится сборка вектора [math] \bar y_{i+1} [/math] на каждом ПЭ. Если необходимо продолжить вычислительный процесс, то полагается [math] i = i + 1 [/math] и осуществляется переход на п. 1

Заметим, что данный алгоритм обладает конечным параллелизмом, но не массовым, так как циклы алгоритма являются информационно зависимыми.

На каждом ярусе в данном алгоритме каждый ПЭ производит четыре операции вычисления правых частей ОДУ, шестнадцать операций сложения векторов и умножения вектора на число, а так же р-1 пересылку данных между другими ПЭ, что довольно сильно замедляет выполнение алгоритма и является накладными расходами при распараллеливании алгоритма. При этом количество итераций цикла равно длине вектора [math] x [/math], то есть [math] n [/math]. Из вышеуказанного следует, что при классификации по высоте ЯПФ алгоритм имеет сложность [math] O(n) [/math], а при классификации по ширине ЯПФ – O(m) (при условии, что [math] p = m [/math]).

1.9 Входные и выходные данные алгоритма

Входными данными алгоритма являются:

1. вектор [math] y^0 [/math] размерности [math] m [/math];
2. границы временного интервала [math] a [/math] и [math] b [/math];
3. частота дискретизации [math] n [/math];

Всего размер входных данных: [math] m + 3 [/math]

Выходными данными являются

1. [math] n [/math] векторов [math] \bar y_i [/math] размерности [math] m [/math];
2. вектор [math] \bar x [/math] размерности [math] n [/math]

Всего размер выходных данных: [math] (m+1)n [/math]

1.10 Свойства алгоритма

Перечислим основные свойства алгоритма:

• Точность. Как следует из названия, у метода Рунге-Кутты 4-го порядка ошибка на конечно интервале интегрирования имеет порядок [math]\mathcal{O}(h^{4})[/math], где [math]h[/math] – расстояние между узлами, в которых вычисляется искомая функция.
• Устойчивость. Метод имеет интервал абсолютной устойчивости [math](-2.78; 0)[/math]. (Определение понятия интервала абсолютной устойчивости можно найти в учебном пособии .)
• Отношение числа расчётов функции, стоящей в правой части задачи Коши, при последовательном алгоритме к числу расчётов при параллельном равняется [math]p[/math], где [math]p[/math] число, используемых процессорных элементов. То есть при увеличении числа используемых процессорных элементов скорость расчётов увеличивается, но стоит учитывать, что число пересылок данных между процессами при этом резко увеличивается также и, в свою очередь, замедляет работу программы.
• Если известен класс функций, которые могут стоять в правой части задачи Коши, то алгоритм можно эффективно модифицировать, чтобы избавиться от лишних пересылок данных.
• Количество операций алгоритма равно [math] n(m-1) [/math] при этом совокупность входных и выходных параметров равняется [math] mn + n + m +4 [/math]. Это означает, что вычислительная мощность алгоритма стремиться к 1 при увеличении размерности задачи.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

Проведём исследование масштабируемости параллельной реализации метода Рунге - Кутты согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Исследовалась собственная параллельная реализация алгоритма, написанная на языке C++ с использованием стандарта MPI. Сборка программы производилась при помощи компилятора компании Intel версии 15.0 (без указания ключей компиляции) с использованием библиотеки OpenMPI версии 1.8.4 . Расчеты проводились на узлах из группы T-Blade2 с процессорами Intel Xeon 5570 Nehalem 2.93GHz, при этом для каждого MPI - процесса выделялось одно ядро.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [4 : 100] с шагом по степеням двойки до 64, далее с шагом 10;
• размерность системы [4 : 7000].

В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 0.0000032%;
• максимальная эффективность реализации 0.0024%.

Перечислим некоторые особенности тестируемой параллельной реализации:

• для тестирования использовалась псевдослучайная правая часть системы, состоящая из суперпозиций случайно выбранных элементарных функций;
• начальные значения искомой функции задавались случайным образом;
• так как в общем случае правая часть системы неизвестна, то не представляется возможным измерять производительность в гигафлопсах; в качестве показателя производительности использовалось количество точек, в которых была вычислена функция.

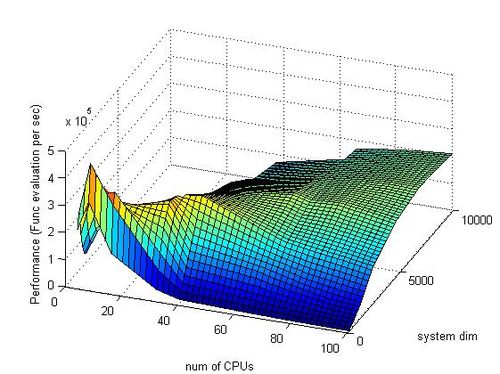
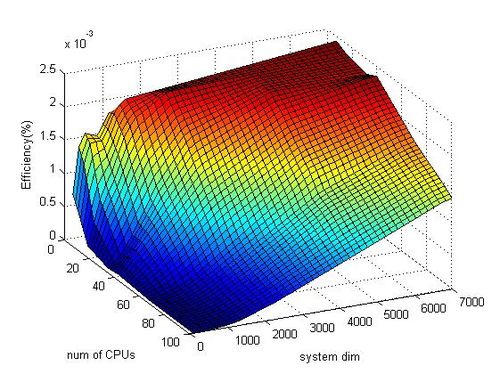
На следующих рисунках приведены графики производительности и эффективности параллельной реализации метода Рунге-Кутты в зависимости от изменяемых параметров запуска.

Рисунок 2. Изменение производительности параллельного алгоритма в зависимости от размерности системы и числа процессоров.

Рисунок 3. Эффективность работы параллельного алгоритма в зависимости от размерности системы и числа процессоров.

Построим оценки масштабируемости протестированной параллельной реализации метода Рунге - Кутты 4-го порядка:

• По числу процессов -0.000000768. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается, однако уменьшение достаточно медленное, что связано с крайне низкой максимальной эффективностью работы параллельной реализации алгоритма. Уменьшение эффективности при увеличении числа процессов для систем с небольшой размерностью объясняется тем, что при количестве процессов превышающем размерность системы часть из них не будет участвовать в вычислениях. Для систем с большой размерностью увеличение процессов негативно сказывается на эффективности, так как увеличивается количество пересылок между ними, что существенно затормаживает работу.

• По размеру задачи 0.000000763. При увеличении размерности системы при фиксированном количестве процессов эффективность на рассмотренной области изменений параметров запуска увеличивается, причём увеличение наблюдается на почти всей рассматриваемой области. Это объясняется тем, что при фиксированном количестве процессов увеличение размерности системы приводит к увеличению вычислительной нагрузки на каждый процессор, вследствие чего увеличивается время вычислительной работы относительно времени простоя. С увеличением числа процессов скорость возрастания эффективности при увеличении размерности задачи уменьшается, так как количество пересылок становится достаточно большим.

• По двум направлениям 0.00000000174. При одновременном увеличении количества процессов и размерности системы эффективность увеличивается. Скорость возрастания эффективности крайне низкая, что объясняется высокими накладными расходами.

Исследованная параллельная реализация на языке C++

2.7 Существующие реализации алгоритма

Метод 4-го порядка является самым часто используемым из всех схем Рунге - Кутты, поэтому существует множество его программных последовательных реализаций как коммерческих, так и бесплатных. Одной из самых известных программных реализаций является ode45 в среде MATLAB, у которой имеется большое количество возможностей для настройки численного расчёта, что делает её достаточно удобной для использования. Также метод Рунге - Кутты 4-го порядка реализован в параллельной библиотеке PETSc, которая является свободно распространяемой. Несмотря на то, что в этой библиотеки большинство методов реализовано с использованием параллельных алгоритмов, метод Рунге - Кутта в ней реализован последовательным. Довольно трудно найти параллельную реализацию метода в случае рассмотрения общей задачи Коши, но существует множество научных работ, в которых описываются параллельные реализации метода Рунге - Кутты для конкретных классов систем, например, в работе А.В. Старченко описывается параллельная реализация для линейных систем.

3 Литература

<references \>