Участник:Ashabokov 415/Алгоритм быстрой сортировки

Алгоритм быстрой сортировки

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Быстрая сортировка, сортировка Хоара — широко известный алгоритм сортировки, разработанный английским информатиком Чарльзом Хоаром во время его работы в МГУ в 1960 году.

Один из самых быстрых известных универсальных алгоритмов сортировки массивов: в среднем [math] O (n \log n) [/math] обменов при упорядочении [math] n [/math] элементов; из-за наличия ряда недостатков на практике обычно используется с некоторыми доработками. Фактически данный алгоритм является улучшением алгоритма сортировки прямого обмена (см. ниже).

1.2 Математическое описание алгоритма

Алгоритм состоит из трех основных шагов:

1. Выбрать опорный элемент (см. ниже). Пусть это будет элемент [math] a' [/math].

2. Используя операции сравнения элементов массива с опорным и перестановки элементов массива, привести исходный массив к виду: [math] a_1 ... a_m a' a_{m+2} ... a_n [/math], где [math] a_j \lt a', j = 1 ... m [/math], [math] a_i \geq a', i = (m+1) ... n [/math], где [math] n [/math] — длина массива.

3. Рекурсивно применить алгоритм к каждому из массивов: [math] a_1 ... a_m [/math] и [math] a_{m+1} ... a_n [/math].

Рассмотрим подробнее метод сравнения и перестановки данных в массиве, применяющийся на шаге 2. Для этого часто используют так называемое разбиение Хоара . Суть данного метода заключается в следующем: выбираются два указателя, указывающие на первый и последний элементы массива соответственно, пусть для наглядности это будут [math] i = 1 [/math] и [math] j = n [/math]. Далее начинаем сдвигать левый указатель вправо, а правый — влево до тех пор, пока выполнены условия: [math] a_i \lt a', a_j \geq a', i \lt j [/math], где [math] a' [/math] — опорный элемент. Как только найдутся такие [math] i, j [/math], что [math] a_i \geq a', a_j \lt a' [/math] и [math] i \lt j [/math], производим перестановку этих двух элементов. Продолжаем этот процесс до тех пор, пока выполнено [math] i \lt j [/math].

1.3 Вычислительное ядро алгоритма

Вычислительным ядром данного алгоритма являются операции сравнения и перестановки [math] i[/math]-ого и [math]j[/math]-ого элементов массива на каждой итерации рекурсивного алгоритма.

Сложность операции разделения массива на два подмассива (сравнение и перестановка элементов массива относительно опорного элемента) занимет время [math] O (log_2 n) [/math].

1.4 Макроструктура алгоритма

Как и написано выше, в разделе "Вычислительное ядро алгоритма", основную часть данного метода сортировки составляет операция разделения массива относительно опорного элемента, которая в свою очередь состоит из операций сравнения и перестановки.

1.5 Схема реализации последовательного алгоритма

1. Случайным образом выбрать опорный элемент массива.

2. Сравнить все элементы сортируемого массива с опорным и разделить исходный массив на два подмассива: с элементами меньше опорного и с элементами больше или равными опорному.

3. Рекурсивно повторить алгоритм для получившихся подмассивов.

Случайный выбор опорного элемента считается наиболее эффективным, так как при фиксировании позиции опорного элемента (например, в качестве опорного всегда берется элемент, стоящий на первой позиции) может привести к существенному снижению эффективности для массивов определенного вида из-за неравномерного распределения элементов в получившихся подмассивах. Также в качестве опорного элемента можно выбирать медиану массива, но считается, что вычисление медианы на каждой итерации рекурсивного алгоритма — слишком затратная операция.

1.6 Последовательная сложность алгоритма

Последовательная сложность данного алгоритма зависит от глубины рекурсии, что в свою очередь зависит от того, насколько удачно были выбраны опорные элементы на каждом витке рекурсии. Рассмотрим несколько возможных случаев.

1. В наилучшем случае выбор опорного элемента на каждом витке рекурсии происходит таким образом, что в результате разбиения исходного массива образуются подмассивы одинаковой длины (с точностью до одного элемента). В таком случае глубина рекурсии составит [math] log_2 n [/math], следовательно, общая сложность алгоритма равна [math] O(n log_2 n) [/math].

2. В наихудшем случае каждое разбиение приводит к образованию подмассивов длины [math] 1 [/math] и [math] n - 1[/math] соответственно. Общая сложность алгоритма в таком случае равна [math] O(n^2) [/math].

1.7 Информационный граф

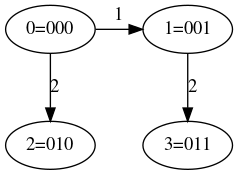
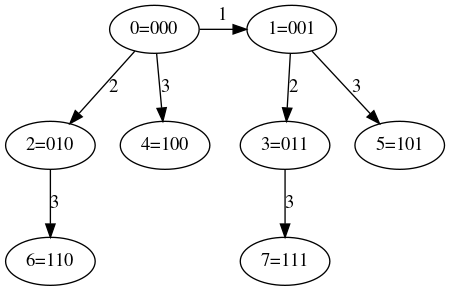
Так как для проведения вычислений задействовано [math] p = 2^N [/math] процессоров, можно воспользоваться следующим алгоритмом распределения данных между процессорами. Распределим произвольным образом данные между процессорами, далее выбираем некоторым образом ведущий элемент и рассылаем его всем процессорам системы. Т.к. топология системы имеет вид n-мерного куба, номер каждого процессора имеет двоичное представление длины [math]n[/math], следовательно, можно ввести правило: на каждом процессоре происходит сравнение имеющегося блока данных с текущим ведущим элементом, после чего элементы меньше ведущего отправляются от процессора с номером [math]n_1[/math] процессору номер [math]n_2[/math], где [math]n_1[/math] отличается от [math]n_2[/math] только в n-том разряде двоичного представления, в двоичном представлении числа [math]n_1[/math] на n-той позиции стоит 1, а [math]n_2[/math] — [math]0[/math]. Таким образом, после данной операции все данные будут разделены между процессорами, образующими [math]n-1[/math]-мерные кубы таким образом, что элемент блока данных любого процессора из первого куба больше любого элемента блока данных процессора из второго куба. Повторив аналогичные действия для каждого из [math]n-1[/math]-мерных кубов, получим 4 [math]n-2[/math]-мерных куба и т.д.

Для наглядности приведем пример: пусть [math] p = 2^3 = 8 [/math]. Ниже приведены графы, иллюстрирующие распределение данных на каждой итерации.

Рисунок 1. Итерация 1.

Рисунок 2. Итерация 2.

Рисунок 3. Итерация 3.

1.8 Ресурс параллелизма алгоритма

Основной идеей данного алгоритма является разбиение всего массива данных на блоки меньшего размера таким образом, что между соответствующими блоками после разбиения можно установить отношение упорядоченности. Сортировка производится следующим образом: выбирается некоторым образом ведущий элемент, после чего происходит разделение исходного массива данных на два блока относительно ведущего элемента: в первый блок помещаются элементы, меньшие ведущего, а во второй — большие ведущего. Таким образом, можно утверждать, что наибольший элемент первого блока меньше наименьшего элемента второго блока. Это означает, что повторив эту операцию для каждого из блоков отдельно некоторое количество раз и объединив результаты, получим массив с исходными данными в отсортированном виде. Из описания становится очевидно, что данный алгоритм можно легко обобщить для параллельной вычислительной системы с количеством процессоров [math]p = 2^n[/math]. Для этого алгоритм необходимо лишь дополнить методом выбора процессоров, между которыми будут происходить обмены данными на i-ом шаге. Подробное описание метода распределения данных между вычислительными узлами можно найти в разделе 1.7. Последним этапом работы алгоритма является объединение разрозненных блоков отсортированных данных в единый массив в правильном порядке. Порядок объединения не трудно восстановить исходя из двоичных представлений номеров процессоров.

Очевидно, что наиболее медленной операцией в описанной выше схеме является операция обмена данными между процессорами, следовательно, хотелось бы получить некоторую оценку количества обменов. Такая оценка приведена ниже:

[math]\sum_{i=1}^{n} i = n(n+1)/2 ≈ \log^2 p [/math] ,

где [math] p [/math] — количество задействованных процессоров.

1.9 Входные и выходные данные алгоритма

Входные данные: любая числовая последовательность произвольной конечной длины. Так как параллельный алгоритм предполагает выбор разделяющего элемента случайным образом, построение последовательностей специального вида не приводит к увеличению вероятности неравномерного распределения данных между вычислительными узлами. Это значит, что эффективность алгоритма не зависит от вида входной последовательности.

Выходные данные: последовательность чисел в отсортированном виде.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализация

Проведём исследование масштабируемости параллельной реализации алгоритма быстрой сортировки согласно методике. Исследование проводится для числа процессоров [8 : 128] с шагом 8.

Рисунок 4. Изменение эффективности в зависимости от числа процессоров и входных данных.

Далее построим оценку масштабируемости:

1. По числу процессоров: 1.0581. Это значит, что с увеличением количества задействованных процессоров эффективность увеличивается. Такое поведение можно объяснить тем, что при увеличении числа процессоров размер сортируемого участка массива для каждого отдельного процессора уменьшается.

2. По числу входных данных: -0.6059. Это значит, что с ростом размеров входных данных эффективность алгоритма падает. Это можно объяснить тем, что при алгоритм предполагает многократный обмен массивами данных, а это значит, что при увеличении размера задачи накладные расходы на обмен данными между процессорами тоже сильно возрастает.

3. По двум направлениям: 0.0386. Это значит, что с ростом числа процессоров и размерами входных данных эффективность все же возрастает, но скорость не слишком велика.

2.7 Существующие реализации алгоритма

Реализация алгоритма быстрой сортировки имеется во многих стандартных библиотеках. Например, для языков программирования C и C++ этот алгоритм можно найти в стандартных библиотеках stdlib.h и cstdlib соответственно. В языке программирования Python имеется встроенная функция sorted(). Язык программирования Java содержит реализацию данного алгоритма в библиотеке java.util. Также реализацию этого алгоритма можно найти в пакете LAPACK DLASRT.