Участник:Dlitvinov/Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией

Авторы статьи: Литвинов Д.А., 611, Шер А.В., 628. Авторы внесли равнозначный вклад в написание статьи.

Алгоритм Ланцоша для арифметики с плавающей точкой с выборочной ортогонализацией
Последовательный алгоритм
Последовательная сложность	$O(kn^2 + k^2n)$
Объём входных данных	$n^2 + n + 1$
Объём выходных данных	$nk$
Параллельный алгоритм
Высота ярусно-параллельной формы	$O(kn + k^2)$
Ширина ярусно-параллельной формы	$O(n)$

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша применяется для поиска небольшого числа собственных значений большой разреженной симметричной матрицы и объединяет метод Ланцоша для построения крыловского подпространства с процедурой Рэлея-Ритца интерпретации собственных значений некоторой вычисляемой матрицы как приближений к собственным значениям заданной матрицы.

Пусть $Q = [Q_k,Q_u]$ - ортогональная матрица порядка $n$, причем $Q_k$ и $Q_u$ имеют соответственно размеры $n \times k$ и $n \times (n-k)$. Столбцы матрицы $Q_k$ вычисляются методом Ланцоша. Запишем следующие соотношения:

$T = Q^T A Q = [Q_k, Q_u]^T A [Q_k, Q_u] = \left[ \begin{array}{cc} Q_k^T A Q_k & Q_k^T A Q_u\\ Q_u^T A Q_k & Q_u^T A Q_u \end{array} \right] = \left[ \begin{array}{cc} T_{k} & T_{ku}^T\\ T_{ku} & T_{u} \end{array} \right]$

Метод Рэлея-Ритца заключается в интерпретации собственных значений матрицы $T_k = Q_k^T A Q_k$ как приближенных к собственным значениям матрицы $A$. Эти приближения называются числами Ритца. Если $A = V \Lambda V^T$ есть спектральное разложение матрицы $T_k$, то столбцы матрицы $Q_k V$ являются приближениями соответствующих собственных векторов и называются векторами Ритца.

Числа и векторы Ритца являются оптимальными приближениями к собственным значениям и собственным векторам матрицы $A$: минимум величины $\Vert A P_k - P_k D \Vert_2$ достигается при $P_k = Q_k V$ и $D = \Lambda$ и равен $\Vert T_ku \Vert_2$.

При применении метода Ланцоша в арифметике с плавающей точкой ортогональность в вычисленных векторах Ланцоша $q_k$ пропадает из-за ошибок округления. Для того чтобы поддерживать ортогональность, проводится повторный процесс ортогонализации Грама-Шмидта. Доказано, что векторы $q_k$ теряют ортогональность весьма систематическим образом, приобретая большие компоненты в отношении уже сошедшихся векторов Ритца. Поэтому можно выборочно ортогонализировать векторы $q_k$ вместо того, чтобы на каждом шаге ортогонализировать вектор ко всем более ранним векторам, как это делается при полной ортогонализации. Таким образом достигается очень высокая степень ортогонализации векторов Ланцоша, и затрачивается очень небольшая дополнительная работа.

1.2 Математическое описание алгоритма

Пусть $A$ - заданная симметричная матрица, $b$ - вектор начального приближения метода Ланцоша. Тогда алгоритм Ланцоша вычисления собственных векторов и собственных значений матрицы $A$ с выборочной ортогонализацией записывается следующим образом:

$\begin{align} q_1 = & b / \Vert b \Vert_2, \; \beta_0 = 0,\; q_0 = 0\\ for \; & j = 1 \; to \; k \\ & z = A\,q_j\\ & \alpha_j = q_j^T z\\ & z = z - \alpha_j q_j - \beta_{j-1}q_{j-1}\\ & for \; i \le k \\ & \; \; \; if \; \beta_k \|v_i (k)\| \le \sqrt{\epsilon} \Vert T_k \Vert_2\\ & \; \; \; \; \; \; z = z - (y_{i,k} ^ T z) y_{i,k}\\ & end \; for\\ & \beta_j = \Vert z \Vert_2\\ & if \; \beta_j = 0 \; then\\ & \; \; \; Quit\; the\; algorithm\\ & q_{j+1} = z / \beta_j\\ end \; & for \end{align}$

Где $v_i$ - это столбцы ортогональной матрицы $V$ из спектрального разложения $T_k = V \Lambda V^T$, а $y_{k,i} = Q_k v_i$ - столбцы матрицы $Q_k V$ - векторы Ритца.

Согласно теореме Пейджа, $y_{k,i}^T q_{k+1} = O(\epsilon \Vert A \Vert_2) / \beta_k \Vert v_i(k) \Vert$, то есть компонента $y_{k,i}^T q_{k+1}$ вычисленного вектора Ланцоша $q_{k+1}$ в направлении вектора Ритца $y_{k,i} = Q_k v_i$ обратно пропорциональна величине $\beta_k \Vert v_i(k) \Vert$, являющейся оценкой погрешности для соответствующего числа Ритца. Поэтому, когда число Ритца сходится, а его оценка погрешности приближается к нулю, вектор Ланцоша приобретает большую компоненту в направлении вектора Ритца $q_{k,i}$, и следует произвести процедуру переортогонализации.

Величина погрешности $\beta_k \Vert v_i(k) \Vert$ считается малой, если она меньше, чем $\sqrt{\epsilon} \Vert A \Vert_2$, так как в этом случае, согласно теореме Пейджа, компонента $\Vert y_{i,k}^T q_{k+1} \Vert = \Vert y_{i,k}^T z \Vert / \Vert z \Vert_2$ скорее всего превосходит уровень $\sqrt{\epsilon}$ (на практике используется $\Vert T_k \Vert_2$ вместо $\Vert A \Vert_2$, так как первое известно, а второе не всегда).

1.3 Вычислительное ядро алгоритма

У описанного алгоритма два ядра, на которые приходится основное время работы алгоритма:

• Вычисление вектора $z = A q_j : O(n^2)$ операций умножения
• Выборочная переортогонализация $z = z - (y_{i,k} ^ T z) y_{i,k} : O(n k^2)$ операций умножения (на практике коэффициент маленький, что обеспечивает бОльшую скорость выполнения алгоритма, чем в случае с полной переортогонализацией)

1.4 Макроструктура алгоритма

Макроструктура алгоритма Ланцоша с выборочной переортогонализацией представляется в виде совокупности метода Ланцоша с выборочной переортогонализацией построения крыловского подпространства и процедуры Рэлея-Ритца.

Каждая итерация первого этапа может быть разложена на следующие макроединицы:

• Умножение матрицы на вектор
• Вычисление скалярного произведения векторов
• Умножение векторов на числа и вычитание векторов
• При выполнении условия необходимости переортогонализации – перемножение и вычитание векторов
• Вычисление нормы вектора
• Умножение вектора на число

Второй этап, процедура Рэлея-Ритца, заключается в нахождении собственных значений и собственных векторов матрицы и интерпретации их как приближенных значений собственных чисел и собственных векторов исходной матрицы, он может быть выполнен любым способом, например, QR-итерацией.

1.5 Схема реализации последовательного алгоритма

На вход алгоритму подаются исходная матрица $A$, вектор начального приближения $b$ и число $k$. Далее последовательно выполняются итерационно для всех $j: 1 \le j \le k$ следующие шаги:

1. Умножается матрица на вектор для нахождения вектора $z$
2. Вычисляется коэффициент $\Alpha_j$ посредством скалярного перемножения векторов
3. Вычисляется новое значение вектора $z$
4. Производятся оценка погрешностей $\beta_k \Vert v_i(k) \Vert$ и выборочная переортогонализация
5. Вычисление очередного значения $\beta_j$ - норма вектора $z$
6. Вычисление и добавление к матрице $Q$ нового столбца
7. Вычисление собственных значений и собственных векторов матрицы $T_j$

1.6 Последовательная сложность алгоритма

• Вычисление вектора $z$ - $n^2$ операций умножения и $n(n-1)$ операций сложения
• Вычисление скалярного произведения векторов - $n$ операций умножения и $(n-1)$ сложений
• Вычисление вектора $z$ - $2n$ умножений и $2n$ сложений
• Оценка погрешностей - $kn$ операций умножения
• Выборочная переортогонализация - $O(2nj)$ умножений и $O(2j(n-1) + n)$ сложений
• Вычисление нормы вектора - $n$ операций умножения и $(n-1)$ сложений
• Вычисление нового столбца матрицы $Q$ - $n$ операций умножения

Итого на каждой итерации:

• Умножений: $n^2 + n + 2n + kn + O(2nj) + n + n = n^2 + 5n + kn + O(2nj)$
• Сложений: $n(n-1) + n-1 + 2n + O(2j(n-1) + n) + n-1 = n^2 + 3n + O(2j(n-1) + n) -2$

Итого за все время выполнения алгоритма:

• Умножений: $kn^2 + 5kn + k^2n + O(k^2n + kn)$
• Сложений: $kn^2 + 3kn + O((k^2+k)(n-1)+kn) = kn^2 + 3kn + O(k^2(n-1)+2kn-k)$

Суммарная последовательная сложность алгоритма - $O(kn^2 + k^2n)$.

1.7 Информационный граф

Ниже представлен граф одной итерации алгоритма с разделением на $n$ потоков.

Рисунок 1. Детальный граф алгоритма Ланцоша с выборочной переортогонализацией.

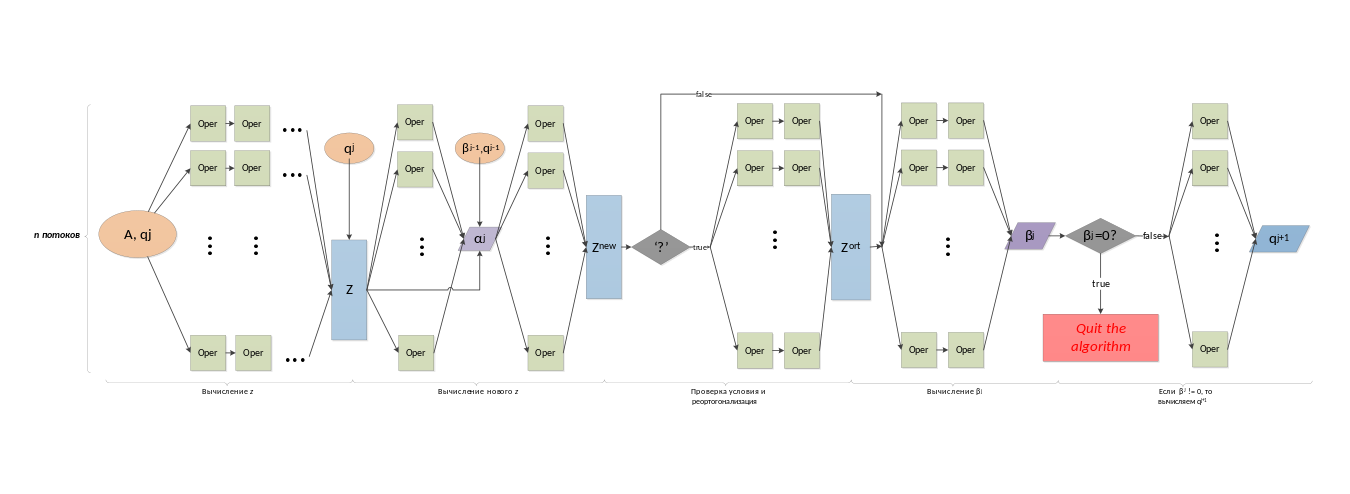
Oper - простая операция сложения/вычитания/умножения/деления с числами с плавающей точкой.
'?' - проверка условия на необходимость переортогонализации.

На вход итерации подается матрица $A$ и вектор $q_j$, на выходе получаем новый вектор $q_{j+1}$.

1.8 Ресурс параллелизма алгоритма

На каждой из итераций алгоритма можно получить выигрыш за счет распараллеливания следующих шагов:

• Вычисление вектора $z$ - умножение матрицы размера $n \times n$ на вектор длины $n$ - $n$ ярусов сложений, $n$ операций умножений в каждом
• Вычисление коэффициента $\alpha_j$ - скалярное произведение векторов - $n$ ярусов сложений, 1 операция умножения в каждом
• Вычисление нового значения вектора $z$: 2 яруса умножений длины $n$ (умножение вектора на число), 2 яруса вычитаний длины $n$
• Выборочная переортогонализация: последовательно для всех $i \le k$ выполняется $j$ ярусов сложений, $n$ операций умножений в каждом, $n$ ярусов сложений, $j$ операций умножений в каждом, один ярус вычитаний размера $n$
• Вычисление $\beta_j$ - скалярное произведение векторов - $n$ ярусов сложений, 1 операция умножения в каждом
• Вычисление $q_j$ - деление вектора на число - один ярус делений размера $n$

Сложность алгоритма по ширине ЯПФ - $O(n)$.

1.9 Входные и выходные данные алгоритма

Входные данные: вещественная матрица $A$ размера $n \times n$, вектор $b$ длины $n$, число $k$

Объем входных данных: $n^2 + n + 1$

Выходные данные: матрица $Q$ размера $n \times k$

Объем выходных данных: $nk$

1.10 Свойства алгоритма

• Соотношение последовательной и параллельной сложности алгоритма равно $n$, что говорит о том, что параллельная реализация теоретически должна давать ощутимый выигрыш
• Вычислительная мощность алгоритма - отношение числа операций к суммарному объему входных и выходных данных - примерно равно $2k$
• Алгоритм устойчив, так как операция переортогонализации как раз направлена на исключение проблемы округления вычисляемых значений
• Алгоритм не является детерминированным, так как, во-первых, используется для разряженных матриц, и, во-вторых, является итерационным с выходом по точности - число операций заранее не определено
• Алгоритм содержит длинные дуги, так как на протяжении всего процесса его выполнения нужно хранить исходную матрицу $A$ и матрицу $Q$ - они нужны на каждой итерации

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Исследование масштабируемости алгоритма проводилось на суперкомпьютере IBM Blue Gene/P ВМК МГУ.

Для тестирования была выбрана реализация BLZPACK. BLZPACK написан на FORTRAN 77 в 2001 году и использует MPI для параллелизма.

Для запуска BLZPACK необходима программа-драйвер. Использовался один из встроенных драйверов DRVMPI (файл drv/double/drvmpi.f) c измененными параметрами -- они меняются в зависимости от размера матрицы и количества требуемых пар собственных значений/векторов. Параметры устанавливаются в начале файла drvmpi.f.

Поскольку в мануале (doc/manual.ps) нету полного описания этих параметров, прокомментируем некоторые из них. Например, для матрицы размера 7500х7500 использовались следующие значения:

      INTEGER          LEIG
      PARAMETER        (LEIG   =     30)

      INTEGER          LISTOR
      PARAMETER        (LISTOR =  15000)

      INTEGER          LN
      PARAMETER        (LN     =    7500)

      INTEGER          LRSTOR
      PARAMETER        (LRSTOR =  10000000)

      INTEGER          NCUV
      PARAMETER        (NCUV   =      1)

      INTEGER          NNZMAX
      PARAMETER        (NNZMAX =  28128750)

      DOUBLE PRECISION ONE
      PARAMETER        (ONE    =  1.0D0)

      DOUBLE PRECISION ZERO
      PARAMETER        (ZERO   =  0.0D0)

• LEIG -- размер массива для хранения полученных собственных

векторов/значений.

• LISTOR -- размер массива ISTOR. Формула определения его минимального размера приведена в мануале.
• LN -- порядок матрицы A, т.е. n.
• LRSTOR -- размер массива RSTOR. Формула определения его минимального размера приведена в мануале.
• NNZMAX -- количество строк во входном файле с матрицей А. Драйвер DRVMPI прочитывает симметричную верхнетреугольную матрицу из файла в координатном формате (строка, столбец, значение); таким образом, для плотной матрицы NNZMAX будет равен $(n^2 + n)/2$

Сам запуск DRVMPI конфигурируется в файле drvsp1.dat -- там задаётся количество требуемых собственных значений/векторов, имя файла со входной матрицей и некоторые другие параметры.

Входные матрицы генерировались следующим простым скриптом на Python 2.7:

import random

if __name__ == "__main__":
    n = 7500
    num_rows = (n*n + n) / 2

    with open('matr7500.data', 'w') as f:
        for i in xrange(1, n + 1):
            j = i  # column number
            while j <= n:
                value = random.uniform(-1, 1)
                f.write("    " + str(i) + "    " + str(j) + "    " + '{:.14e}'.format(value) + "\n")
                j += 1

Был использован компилятор GNU Fortran 77 (g77), точнее, его обертка mpif77 с поддержкой MPI. На Blue Gene/P используется собственная реализация MPI от IBM, основанная на MPICH. Для сборки BLZPACK на Blue Gene/P нужно заменить имя компилятора (ключ FC) в файле sys/MACROS/Linux на mpif77 и запустить ./creator -f -mpi в корне проекта. После этого можно собрать драйвер, зайдя в директорию drv/data и выполнив make drvmpi.x.

Использовался SMP-режим работы Blue Gene/P, когда на каждом вычислительном узле выполняется всего один MPI-процесс.

Пример запуска программы:

mpisubmit.bg -n 64 -w 00:15:00 -m smp  --stdout eigen.out --stderr eigen.err drvmpi.x

Тестировались следующие конфигурации:

• Порядок матриц 1000, 2500, 5000, 7500
• Количество процессоров 4, 8, 16, 32, 64, 128

У матрицы размера 1000 производился поиск 100 пар собственных векторов/значений, у остальных -- 30 пар. Результаты приведены в таблице 1:

Табл. 1. Результаты тестирования. В ячейках таблицы -- время работы алгоритма в секундах.

		Число процессоров
		4	8	16	32	64	128
Размер матрицы	1000	24	17	14	15	16	21
	2500	48	27	18	13	12	13
	5000	207	92	61	37	24	23
	7500	612	298	153	90	50	42

Заметно, при всех размерах матриц алгоритм перестает масштабироваться начиная с некоторого числа процессоров: для матрицы размера 1000 это 32 узла, для матрицы размера 2500 64 узла и т.д. Это связано с тем, что затраты на коммуникацию между узлами становится больше, чем выгода от распараллеливания вычислений. При меньшем же количестве процессоров алгоритм хорошо масштабируется, соответствуя теоретически вычисленной высоте ярусно-параллельной формы $O(kn + k^2)$

2.7 Существующие реализации алгоритма

Неплохой обзор существующих реализаций находится здесь: A Survey of Software for Sparse Eigenvalue Problems

Ниже будут перечислены только те реализации, которые поддерживают именно выборочную ортогонализацию.

• BLZPACK FORTRAN 77, MPI. 2000 год.
• BLKLAN C, MATLAB. Нет поддержки параллелизма. 2003 год.
• PROPACK FORTRAN 77, MATLAB. OpenMP. Предназначен для нахождения SVD разложения, но алгоритм Ланцоша может быть вызван и напрямую. 2005 год.
• LANZ FORTRAN 77. Нет поддержки параллелизма. 1991 год.
• SVDPACK C, FORTRAN 77. Нет поддержки параллелизма. Предназначен для нахождения SVD разложения. 1992 год.

3 Литература

• Дж. Деммель, Вычислительная линейная алгебра. Теория и приложения. Пер. с англ. - М.: Мир, 2001.