Участник:Egor Luckjanow 403/Алгоритм Грамма-Шмидта

Автор: Егор Лукьянов, студент 403 группы ВМК МГУ

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм Грама-Шмидта предназначен для построения QR-разложения матрицы.

1.2 Математическое описание алгоритма

В основе работы алгоритма лежит метод Грама-Шмидта для построения ортонормированного базиса на основе уже существующего:
[math]q_1 = \frac{a_1}{||a_1||}[/math]
[math]p_2 = a_2 - (a_2, q_1)q_1[/math]
[math]q_2 = \frac{p_2}{||p_2||}[/math]
[math]p_3 = a_3 - (a_3, q_1)q_1 - (a_3, q_2)q_2[/math]
[math]q_3 = \frac{p_3}{||p_3||}[/math]
[math]...[/math]
Мы применяем этот метод к столбцам исходной матрицы A и получаем разложение A = QR, где Q составлена из столбцов q_1,...,q_n, полученных в результате применения метода Грама-Шмидта, а R -- матрица коэффициентов, которая будет верхнетреугольной в силу вида метода.

1.3 Вычислительное ядро алгоритма

Ядро алгоритма -- последовательное нахождение Q и R, как в математическом описании.

1.4 Макроструктура алгоритма

Макрооперации: скалярное произведение ddot; умножение матрицы на вектор с прибавлением другого вектора daxpy.

1.5 Схема реализации последовательного алгоритма

void QR(int N, double* A, double* Q, double* R)
{
	int one = 1;
	for (int i = 0; i < N; ++i) {
		R[i * N + i] = 1;
		for (int k = 1; k < i + 1; ++k) {
			R[i - k + i * N] = ddot(&N, A + i * N, &one, Q + (i - k) * N, &one) / ddot(&N, Q + (i - k) * N, &one, Q + (i - k) * N, &one);
		}
		for (int j = 0; j < N; ++j) {
			Q[j + i * N] = A[j + i * N];
		}
		for (int k = 0; k < i; ++k) {
			double tmp = -R[i - k - 1 + i * N];
			daxpy(&N, &tmp, Q + (i - k - 1) * N, &one, Q + i * N, &one);
		}
		for (int k = i + 1; k < N; ++k) {
			R[k + i * N] = 0;
		}
	}
	for (int i = 0; i < N; ++i) {
		double norm = dnrm2(&N, Q + i * N, &one);
		for (int j = 0; j < N; ++j) {
			Q[j + i * N] /= norm;
		}
		for (int j = 0; j < N; ++j) {
			R[i + j * N] *= norm;
		}
	}
}

1.6 Последовательная сложность алгоритма

Сложность последовательного алгоритма -- [math]O(n^3)[/math].

1.7 Информационный граф

1.8 Ресурс параллелизма алгоритма

Параллельная сложность (в терминах операций сложения и умножения) -- [math]O(n^2)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные -- размер матрицы и сама матрица. Выходные данные -- матрицы [math]Q[/math] и [math]R[/math] из QR-разложения поданной на вход матрицы.

1.10 Свойства алгоритма

Алгоритм Грамма-Шмидта обладает свойством потери ортогональности. Поэтому для корректной его реализации необходимо время от времени делать реортогонализацию, а также обеспечить максимально возможную точность вычислений с плавающей точкой. Можно реализовать алгоритм для работы с рациональными матрицами. Тогда проблема с потерей ортогонализации пропадает (в виду идеальной точности вычислений в кольцах вида [math]\mathbb{Z}/\lt m\gt [/math] на компьютере).

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

Проблема с потерей ортогональности уже описана в свойствах алгоритма.

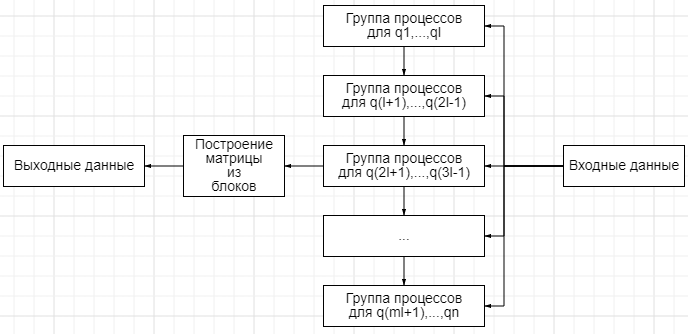
2.3 Возможные способы и особенности параллельной реализации алгоритма

Метод Грамма-Шмидта не предполагает блочной реализации, в которой процессы, обрабатывающие блоки, никак не зависели бы друг от друга. Есть вариант отдать каждому процессу по группе столбцов [math]q_i[/math] для вычисления. Число пересылок тогда составляет [math]n(n+1)/2[/math].

2.3.1 Код возможной реализации

#include <stdio.h>
#include <iostream>
#include <mpi.h>
#include <omp.h>
#include <mkl.h>
#include <cstdlib>

#define world MPI_COMM_WORLD

void gather(int n, double *A, int id, double *q, double *r, int nmon)
{
	double *Q = new double[n * n], *R = new double[n * n];
	MPI_Gather(q, n * nmon, MPI_DOUBLE, Q, n * nmon, MPI_DOUBLE, 0, world);
	MPI_Gather(r, n * nmon, MPI_DOUBLE, R, n * nmon, MPI_DOUBLE, 0, world);
	if (id != 0)
		return;
	#pragma omp parallel for
	for (int i = 0; i < n; ++i)
	{
		int ione = 1;
		double norm = dnrm2(&n, Q + i * n, &ione);
		for (int j = 0; j < n; ++j)
		{
			Q[j + i * n] /= norm;
			R[i + j * n] *= norm;
		}
	}
	double one = 1;
	double zero = 0;
	char trans = 'N';
	double *tmpA = new double[n * n];
	dgemm(&trans, &trans, &n, &n, &n, &one, Q, &n, R, &n, &zero, tmpA, &n);
	int n2 = n * n;
	double mone = -1;
	int ione = 1;
	daxpy(&n2, &mone, A, &ione, tmpA, &ione);
	std:: cout << dnrm2(&n2, tmpA, &ione) << std::endl << std::endl;
	char trans2 = 'T';
	dgemm(&trans, &trans2, &n, &n, &n, &one, Q, &n, Q, &n, &zero, A, &n);
	double *I = new double[n * n];
	for (int i = 0; i < n; ++i)
	for (int j = 0; j < n; ++j)
		if (i == j)
			I[j + i * n] = 1;
		else
			I[j + i * n] = 0;
	daxpy(&n2, &mone, I, &ione, A, &ione);
	std::cout << dnrm2(&n2, A, &ione) << std::endl << std::endl;

}

int main(int argc, char *argv[])
{
	int rinit;
	MPI_Init(&argc, &argv);
	sscanf(argv[1], "%d", &rinit);
	srand(rinit);
	int nproc;
	MPI_Comm_size(world, &nproc);
	int nmon = 20;
	int n = nmon * nproc;
	MPI_Status status;
	double *A = new double[n * n];
	#pragma omp parallel for
	for (int i = 0; i < n; ++i)
	for (int j = 0; j < n; ++j)
		if (i == j)
			A[j + i * n] = rand();
		else
			A[j + i * n] = rand();
	int id;
	int ione = 1;
	MPI_Comm_rank(world, &id);
	double *s = new double[n * nmon];
	double *q = new double[n * nmon], *r = new double[n * nmon];
	for (int i1 = 0; i1 < nmon; ++i1)
	for (int i = 0; i < n; ++i)
		q[i1 * n + i] = A[i + (id * nmon + i1) * n];
	for (int i1 = 0; i1 < nmon; ++i1)
	{
		for (int i = 0; i < id; ++i)
		{
		MPI_Recv(s, n * nmon, MPI_DOUBLE, i, 1, world, &status);
		for (int j = 0; j < nmon; ++j)
		{
			double arg = -ddot(&n, A + (id * nmon + i1) * n, &ione, s + j * n, &ione) / ddot(&n, s + j * n, &ione, s + j * n, &ione);
			daxpy(&n, &arg, s + j * n, &ione, q + i1 * n, &ione);
			r[i1 * n + i * nmon + j] = -arg;
		}
		}
		for (int i = 0; i < i1; ++i)
		{
			double arg = -ddot(&n, A + (id * nmon + i1) * n, &ione, q + i * n, &ione) / ddot(&n, q + i * n, &ione, q + i * n, &ione);
			daxpy(&n, &arg, q + i * n, &ione, q + i1 * n, &ione);
			r[i1 * n + id * nmon + i] = -arg;

		}
		r[i1 * n + id * nmon + i1] = 1;
		for (int i = id * nmon + i1 + 1; i < n; ++i)
			r[i1 * n + i] = 0;
		MPI_Request req;
		#pragma omp parallel for
		for (int i1 = 0; i1 < nmon; ++i1)
		for (int i = id + 1; i < nproc; ++i)
			MPI_Isend(q, n * nmon, MPI_DOUBLE, i, 1, world, &req);
	}
	MPI_Barrier(world);
	gather(n, A, id, q, r, nmon);
	MPI_Finalize();
	return 0;
}

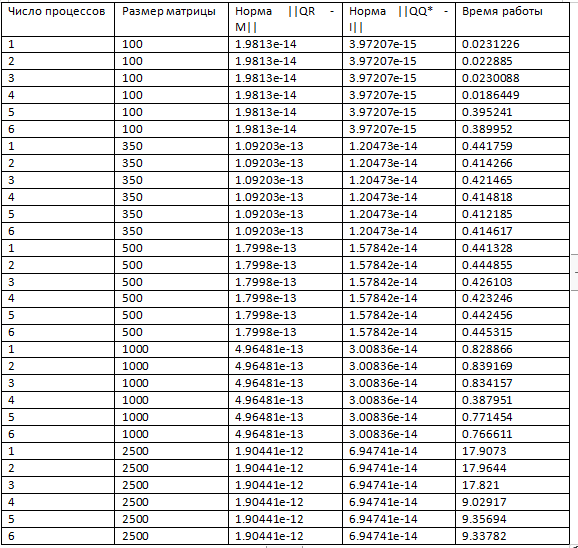
2.3.2 Результаты работы данного кода

2.4 Масштабируемость алгоритма и его реализации

Алгоритм увеличивает время своей работы при добавлении независимых вычислительных ядер. Алгоритм обладает сильной масштабируемостью.

2.5 Динамические характеристики и эффективность реализации алгоритма

При выборе системы для запуска предпочтение следует отдавать скорости обмена данными между процессами. При выборе архитектуры необходимо учесть наличие возможности вычислений с высокой точностью. Параллельный алгоритм не дает разительного превосходства по времени исполнения в сравнении с последовательным, но все же имеет место заметное уменьшение времени исполнения при выполнении указанных условий.

2.6 Выводы для классов архитектур

Реализация архитектурно независима. Зависимы только макрооперации, которые предполагаются уже реализованными.

2.7 Существующие реализации алгоритма

В силу потери ортогональности алгоритм Грамма-Шмидта пользуется небольшой популярностью в сравнении с альтернативными методами QR-разложения, так что популярных параллельных реализаций нет. Альтернативный (не Грамм-Шмидт) метод представлен, например, в пакете LAPACK и является одним из лучших по производительности.

3 Литература

1. Е. Е. Тыртышников, Методы численного анализа
2. Ф. Р. Гантмахер, Теория матриц
3. С. Ленг, Алгебра
4. Е. Е. Тыртышников, Основы алгебры