Участник:Jhuighuy/Уравнение Пуассона, решение методом Галеркина
Уравнение Пуассона, решение методом Галеркина, Бутаков О.Б.
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Метод Галеркина (Галеркина-Бубнова) используется для решения краевых задач дифференциальных уравнений. В данной статье рассмотрим алгоритм метода Галеркина для решения уравнения Пуассона с краевыми условиями первого рода:
- [math] \newcommand{\laplace}{\mathop{}\!\mathbin\bigtriangleup} \begin{cases} \laplace u = -f, u = \phi(x,y,z), (x,y,z) \in G, G = (0,L_x)\times(0,L_y)\times(0,L_z), \\ u(x,y,z) = 0, (x,y,z) \in \partial G. \end{cases} [/math]
Алгоритм предполагает выбор полного набора базисных функций, удовлетворяющих краевым условиям. Решение строится в виде линейной комбинации базисных функций, коэффициенты определяются условием ортогональности невязки базисной функции.
1.2 Математическое описание алгоритма
Выберем тригонометрическую систему базисных функций:
- [math] \phi_{m,n,l} = sin(\frac{\pi m x}{L_x})sin(\frac{\pi n y}{L_y})sin(\frac{\pi l z}{L_z}), m=1..N_x, n=1..N_y, l=1..N_z. [/math]
Очевидно, эта система удовлетворяет краевым условиям. Проверим ортогональность функций, введя скалярное произведение [math](u,v) = \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} u v dx dy dz[/math]:
- [math] (\phi_{m,n,l} \phi_{i,j,k}) = \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} \phi_{m,n,l} \phi_{i,j,k} dx dy dz = \int_{0}^{L_x} sin(\frac{\pi m x}{L_x}) sin(\frac{\pi i x}{L_x}) dx \int_{0}^{L_y} sin(\frac{\pi n x}{L_y}) sin(\frac{\pi j x}{L_y}) dy \int_{0}^{L_z} sin(\frac{\pi l x}{L_z}) sin(\frac{\pi k x}{L_z}) dz = \delta_{m,i}\frac{L_x}{2} \delta_{n,j}\frac{L_y}{2} \delta_{l,k}\frac{L_z}{2}. [/math]
Выражение, представленное выше, с учетом известной ортогональности тригонометрического ряда, дает выражение для нормы базисной функции, которое потребуется в дальнейшем.
Представим приближенное решение в виде комбинации базисных функций:
- [math] \hat{u} = \Sigma_{m,n,l=1}^{N_x,N_y,N_z} C_{m,n,l} \phi_{m,n,l} [/math].
Подставив в уравнение выражение для приближенного решения, получим формулу невязки:
- [math] R(x,y,z) = \laplace\hat{u} + f = -\Sigma_{m,n,l=1}^{N_x,N_y,N_z} C_{m,n,l} \pi^2(\frac{m^2}{L_x^2}+\frac{n^2}{L_y^2}+\frac{l^2}{L_z^2}) \phi_{m,n,l} + f [/math].
Разложив выражение для невязки по базисным функции, потребуем ортогональность невязки базисным функциям:
- [math] \begin{split} &R_{i,j,k} = (R, \phi_{i,j,k}) = -C_{i,j,k} \pi^2(\frac{m^2}{L_x^2}+\frac{n^2}{L_y^2}+\frac{l^2}{L_z^2}) \frac{L_x}{2}\frac{L_y}{2}\frac{L_z}{2} + (f, \phi_{i,j,k}) = 0 \Rightarrow \\ &C_{i,j,k} = \frac{8 L_x L_y L_z (f, \phi_{i,j,k})}{\pi^2 ((i L_y L_z)^2 + (j L_x L_z)^2 + (k L_x L_y)^2)}, i=1..N_x, j=1..N_y. k=1..N_z. \end{split} [/math].
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма состоит из подсчета интегралов для поиска коэффициентов приближенного решения, а также для нахождения приближенного решения на сетке. Опишем сетку:
- [math] \omega_h = [(x_i,y_j,z_k); x_i=i\Delta x, y_j=i\Delta y, z_k=k\Delta k; L_x=M_x\Delta x, L_y=M_y\Delta y, L_z=M_z\Delta z]. [/math]
Тогда трехмерный интеграл будет приближенно описываться выражением:
- [math] \int_{0}^{L_x}\int_{0}^{L_y}\int_{0}^{L_z} f dx dy dz \approx \Sigma_{m,n,l=1}^{M_x,M_y,M_z} f(x_i,y_j,z_k)\Delta x\Delta y\Delta z. [/math]
Вычисление функции на сетке тривиально:
- [math] \hat{u}_{h,i,j,k} = \Sigma_{m,n,l=1}^{N_x,N_y,N_z} C_{m,n,l} sin(\frac{\pi m x_i}{L_x})sin(\frac{\pi n y_j}{L_y})sin(\frac{\pi l z_k}{L_z}). [/math]
1.4 Макроструктура алгоритма
Сначала вычислим все коэффициенты, а потом восстановим функцию. Алгоритм:
- Для всех [math]i=1..N_x, j=1..N_y, k=1..N_z[/math] вычислить [math]C_{m,n,l}[/math].
- Для всех [math]i=0..M_x, j=0..M_y, k=0..M_z[/math] вычислить [math]\hat{u}_{h,i,j,k}[/math].
1.5 Схема реализации последовательного алгоритма
Первый этап на языке Fortran (для наглядности вложенные конструкции упрощены):
Do i j k = 1 1 1, Nx Ny Nz
r = 0.0D0
Do i0 j0 k0 = 1 1 1, Mx My Mz
x = i0*dx
y = j0*dy
z = k0*dz
r = r + dx*dy*dz*f(i0,j0,k0)*Sin(Pi*i*x/Lx)*Sin(Pi*j*y/Ly)*Sin(Pi*k*z/Lz)
End Do
c(i, j, k) = 8*r / (Pi**2*(Ly*Lz/Lx*i**2 + Lx*Lz/Ly*j**2 + Lx*Ly/Lz*k**2))
End Do
Второй этап:
Do i0 j0 k0 = 0 0 0, M_x M_y M_z
x = i0*dx
y = j0*dy
z = k0*dz
s = 0.0D0
Do i j k = 1 1 1, N_x N_y N_z
s = s + c(i, j, k)*Sin(Pi*i*x/Lx)*Sin(Pi*j*y/Ly)*Sin(Pi*k*z/Lz)
End Do
u(i0, j0, k0) = s
End Do
1.6 Последовательная сложность алгоритма
Вычислительную сложность первого варианта алгоритма можно оценить как [math]O(N_x N_y N_z M_x M_y M_z)[/math] операций с плавающей точкой.
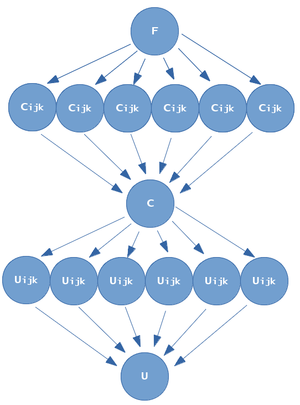
1.7 Информационный граф
- На нулевом ярусе алгоритма происходит генерация или считывание правой части уравнения.
- На первом ярусе вычисляются коэффициенты.
- На втором ярусе происходит объединение их в общий массив.
- На третьем ярусе вычисляется сеточная функция.
- На четвертом ярусе происходит вывод.
1.8 Ресурс параллелизма алгоритма
Информационный граф показывает, что коэффициенты [math]C_{m,n,l}[/math] и [math]\hat{u}_{h,i,j,k}[/math] можно вычислять параллельно. Так как каждое из этих значений вычисляется в виде сумм, дополнительного увеличения производительности можно достичь за счет параллельного суммирования. Таким образом, если [math]P[/math] — количество вычислительных узлов, при [math]P \le min(N_x N_y N_z, M_x M_y M_z)[/math], можно достичь производительности в [math]O(\frac{N_x N_y N_z M_x M_y M_z}{P})[/math] операций.
При [math]P \gt min(N_x N_y N_z, M_x M_y M_z)[/math], положив [math]Q = mod(P, min(N_x N_y N_z, M_x M_y M_z))[/math], за счет параллельного суммирования, эта величина равна [math]O(\frac{N_x N_y N_z + M_x M_y M_z}{Q})[/math].
1.9 Входные и выходные данные алгоритма
В качестве входных данных выступает трехмерный массив [math]M_x \times M_y \times M_z[/math] правой части уравнения. Выходные данные — трехмерный массив решения той же размерности.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
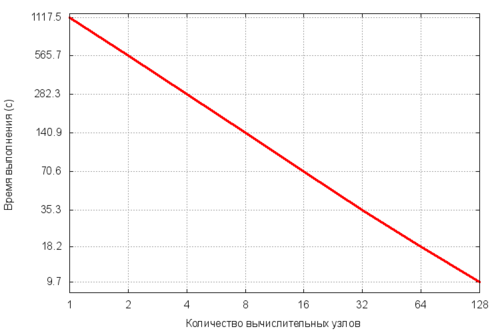
Для оценки масштабируемости были выбраны значения [math]N_x=N_y=N_z=M_x=M_y=M_z=64[/math]. Все тесты проводились на суперкомпьютере Ломоносов-1.
Анализируя график, видно, что производительность растет линейно с увеличением количества вычислительных узлов. Шкала на данном графике логарифмическая. Это можно объяснить отсутствием накладных расходов на обмен данными между процессами (то есть все данные, необходимые для соответствующего вычисления, локальны относительно процесса) при вычислении коэффициентов приближенного решения и значений функции, а также лишь двумя обменами данными между этапами вычислений.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- [1] Реализация метода Галеркина для интегрального уравнения с использованием MPI.
- [2] Реализация метода Галеркина для задач CFD с использованием CUDA.
3 Литература
Абакумов М.В., Гулин А.В. Лекции по численным методам математической физики: Учеб. пособие. - М.:ИНФРА-М,2013
Самарский А. А. Введение в численные методы, 1982.