Участник:Lonalone/Генерация гауссовского вектора методом линейных преобразований

Автор описания: Меньших И. М.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Из многомерных распределений особый интерес представляет нормальное. Этому закону подчиняются все результаты воздействия большого числа случайных факторов, среди которых нет превалирующих.

В статье приведен алгоритм генерации n-мерного гауссовского случайного вектора с помощью метода линейных преобразований. Известно, что случае нормально распределенного случайного вектора, ковариационная матрица вместе с математическим ожиданием этого вектора полностью определяют его распределение. Поэтому для полного статистического соответствия моделируемого и теоретического распределения гауссовского вектора достаточно обеспечить требуемые значения указанных параметров.

Идея алгоритма заключается в линейном преобразовании n-мерного случайного вектора $Y$, компоненты которого независимы и одинаково распределены по нормальному закону со стандартными параметрами, в случайный вектор $X$ с требуемыми ковариационной матрицей и вектором математических ожиданий.

1.2 Математическое описание алгоритма

1.2.1 Метод линейных преобразований

Даны ковариационная матрица $\Sigma$ и вектор математических ожиданий $M$:

$\Sigma = \|\sigma_{ij}\| = \| \mathbb{E}[(X_{i} - m_{x_{i}})(X_{j} - m_{x_{j}})]\|, \\ M = (m_{x_{1}}, m_{x_{2}}, ..., m_{x_{n}})^T.$

Требуется найти такую матрицу $B$, которая позволяла бы получить искомый вектор $X$ с требуемыми характеристиками в результате линейного преобразования $X = BY + M$, где $Y$ — n-мерный случайный вектор с независимыми нормально распределенными компонентами со стандартными параметрами.

Будем искать матрицу $B$ в виде нижней треугольной матрицы. Перейдем от матричной записи к системе алгебраических уравнений:

$\begin{pmatrix} X_{1} \\ X_{2} \\ \vdots \\ X_{n} \end{pmatrix} = \begin{pmatrix} b_{11} & 0 & \cdots & 0 \\b_{21} & b_{22} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ b_{n1} & b_{n2} & \cdots & b_{nn} \end{pmatrix} \times \begin{pmatrix} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{n} \end{pmatrix} + \begin{pmatrix} m_{x_{1}} \\ m_{x_{2}} \\ \vdots \\ m_{x_{n}} \end{pmatrix} \Rightarrow$

$\begin{cases}X_{1} - m_{x_{1}} = b_{11}Y_{1} \\X_{2} - m_{x_{2}} = b_{21}Y_{1} + b_{22}Y_{2} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\X_{n} - m_{x_{n}} = b_{n1}Y_{1} + b_{n2}Y_{2} + \cdots + b_{nn}Y_{n} \end{cases}$

Поскольку компоненты вектора $Y$ независимы и имеют стандартные параметры, справедливо выражение:

$\mathbb{E}[Y_{i}Y_{j}] = \left\{\begin{matrix} 1, &i = j, \\ 0, &i \not= j. \end{matrix}\right.$

Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы и взяв от результатов перемножения математическое ожидание, получаем систему уравнений вида:

$\begin{cases} \mathbb{E}[(X_{1} - m_{x_{1}})(X_{1} - m_{x_{1}})] = \mathbb{E}[b_{11}Y_{1}b_{11}Y_{1}], \\ \mathbb{E}[(X_{1} - m_{x_{1}})(X_{2} - m_{x_{2}})] = \mathbb{E}[(b_{21}Y_{1} + b_{22}Y_{2})b_{11}Y_{1}], \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \end{cases}$

Таким образом, в левых частях полученной системы уравнений располагаются элементы заданной ковариационной матрицы $\Sigma$, а в правых — элементы искомой матрицы $B$. Последовательно решая эту систему, получаем формулы для расчета элементов $\sigma_{ij}$:

$b_{11}=\sqrt{\sigma_{11}}; b_{21}=\frac{\sigma_{12}}{\sqrt{\sigma_{11}}}; b_{22} = \sqrt{\sigma_{22} - \frac{\sigma_{12}}{\sigma_{11}}}, \cdots$

Рекуррентная формула для расчета любого элемента матрицы преобразования $B$ имеет вид:

$b_{ij} = \frac {\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}} {\sqrt{\sigma_{jj} - \sum_{k=1}^{j-1} b_{jk}^2}}, \quad 1 \leqslant j \leqslant i \leqslant n$

(суммы с верхним нулевым пределом считаются равными нулю)

Таким образом, матрица $B$ получается с помощью разложения Холецкого матрицы $\Sigma$.

1.2.2 Генерация случайного вектора Y

Пусть имеется генератор псевдослучайных чисел (ГПСЧ, PRNG), с помощью которого можно получить реализацию случайной величины $u \sim U(0,1)$. Описанный выше случайный вектор $Y=(y_1, \dots, y_n)$ с независимыми компонентами составим из $n$ реализаций случайной величины $\eta \sim N(0,1)$. Каждую такую реализацию $y_i$, в свою очередь, получим с помощью приближения по ЦПТ $\kappa$ случайными величинами, распределенными равномерно на отрезке [0,1]:

$y_i = \sqrt{\frac{12}{\kappa}} \left(\sum_{j=1}^{\kappa}{u_j^i} - \frac{\kappa}{2}\right), \quad i = \overline{1, n} \\ $

где $u_j^i -$ реализации случайной величины $u$, а $\kappa -$ параметр, обеспечивающий качество приближения.

Как правило, $\kappa$ берут равным $12$ и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма можно составить из множественных (всего $\frac{n(n−1)}{2}$) вычислений следующих выражений, включающих скалярные произведения строк матрицы:

$\sigma_{ij} - \sum_{k=1}^{j-1} b_{ik} b_{jk}, \quad 1 \leqslant j \leqslant i \leqslant n$

1.4 Макроструктура алгоритма

• Заполнение матрицы $B$
• Генерация вектора $Y$
• Вычисление вектора $X = BY + M$

1.5 Схема реализации последовательного алгоритма

1) Заполнение матрицы $B$.

(a) $b_{11}= \sqrt{\sigma_{11}}$

(b) $b_{k1}= \frac{\sigma_{k1}}{l_{11}}$, $\quad k = \overline{2,n}$

Следующие два пункта выполняются циклически, друг за другом для $i = \overline{2,n}$.

(c) $b_{ii} = \sqrt{\sigma_{ii} - \sum_{p = 1}^{i - 1} b_{ip}^2}$

(d) $b_{ji} = \frac{\sigma_{ji} - \sum_{p = 1}^{i - 1} b_{ip} b_{jp}} {l_{ii}}$, $\quad i \neq n, j = \overline{i+1,n}$

2) Генерация вектора $Y$.

Следующие два пункта выполняются циклически, друг за другом для $i = \overline{1,n}$.

(a) $u_j^i \leftarrow PRNG,$ $\quad j = \overline{1,k}$

(b) $y_i = \sqrt{\frac{12}{\kappa}} \left(\sum_{j=1}^{\kappa}{u_j^i} - \frac{\kappa}{2}\right)$

3) Вычисление вектора $X$.

$x_i = m_{x_i} + \sum_{k = 1}^{i} b_{ik} y_{k}, \quad i = \overline{1,n}$.

1.6 Последовательная сложность алгоритма

Для генерации гауссовского случайного вектора порядка $n$ в последовательном варианте требуется:

• $n(n+1) + \frac {n(n-1)(n-2)}{6}$ (умножений)
• $\frac {n(n+1)}{2} + \frac {n(n-1)(n-2)}{6}$ (вычитаний)
• $\frac {n(n-1+2\kappa)}{2}$ (сложений)
• $\frac {n(n+3)}{2}$ (делений)
• $2n$ (вычислений квадратного корня)

$\frac{n}{6}\left(2n^2+9n+31+6\kappa\right)$ - итого операций.

Таким образом, последовательная сложность алгоритма равна $O(n^3)$.

1.7 Информационный граф

1.7.1 Заполнение матрицы B

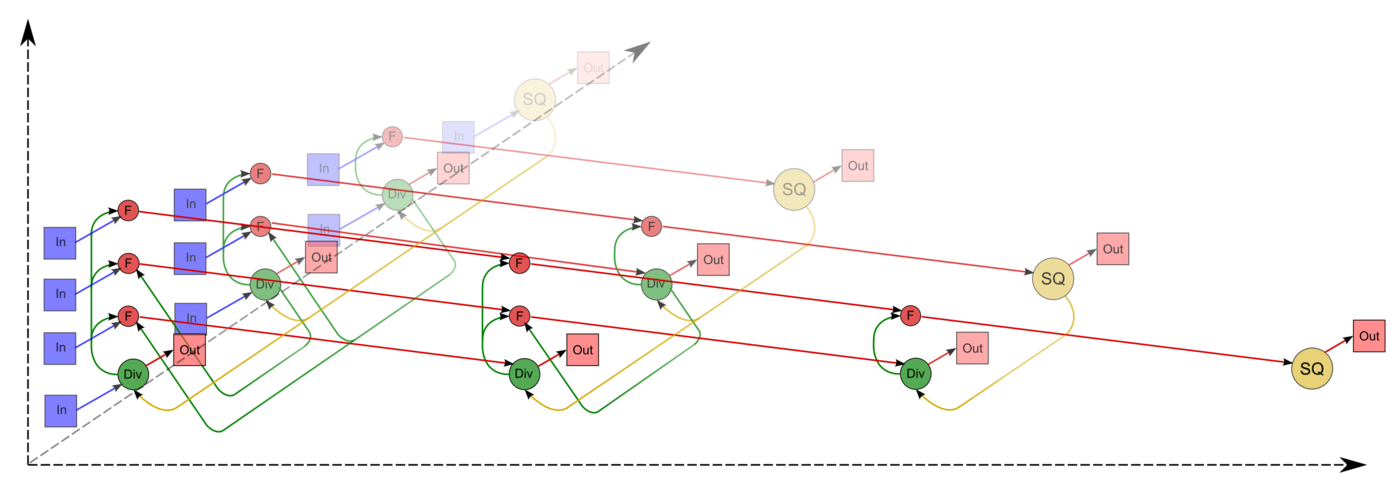
Граф этапа 1 макроструктуры алгоритма (разложения Холецкого) состоит из трёх групп вершин, расположенных в целочисленных узлах трёх областей разной размерности.

Первая группа вершин расположена в одномерной области, соответствующая ей операция вычисляет функцию SQRT. Единственная координата каждой из вершин $i$ меняется в диапазоне от $1$ до $n$, принимая все целочисленные значения.

Аргумент этой функции

• при $i = 1$ — элемент входных данных $\sigma_{11}$;
• при $i \gt 1$ — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами $i - 1$, $i$, $i - 1$.

Результат срабатывания операции является выходным данным $b_{ii}$.

Вторая группа вершин расположена в двумерной области, соответствующая ей операция $a / b$. Естественно введённые координаты области таковы:

• $i$ — меняется в диапазоне от $1$ до $n-1$, принимая все целочисленные значения;
• $j$ — меняется в диапазоне от $i+1$ до $n$, принимая все целочисленные значения.

Аргументы операции следующие:

• $a$:
  • при $i = 1$ — элемент входных данных $\sigma_{j1}$;
  • при $i \gt 1$ — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами $i - 1, j, i - 1$;
• $b$ — результат срабатывания операции, соответствующей вершине из первой группы, с координатой $i$.

Результат срабатывания операции является выходным данным $b_{ji}$.

Третья группа вершин расположена в трёхмерной области, соответствующая ей операция $a - b * c$. Естественно введённые координаты области таковы:

• $i$ — меняется в диапазоне от $2$ до $n$, принимая все целочисленные значения;
• $j$ — меняется в диапазоне от $i$ до $n$, принимая все целочисленные значения;
• $p$ — меняется в диапазоне от $1$ до $i - 1$, принимая все целочисленные значения.

Аргументы операции следующие:

• $a$:
  • при $p = 1$ элемент входных данных $\sigma_{ji}$;
  • при $p \gt 1$ — результат срабатывания операции, соответствующей вершине из третьей группы, с координатами $i, j, p - 1$;
• $b$ — результат срабатывания операции, соответствующей вершине из второй группы, с координатами $p, i$;
• $c$ — результат срабатывания операции, соответствующей вершине из второй группы, с координатами $p, j$;

Результат срабатывания операции является промежуточным данным этапа.

Описанный граф можно посмотреть на рис.1, выполненном для случая $n = 4$.

Рисунок 1. Граф этапа 1 макроструктуры алгоритма. SQ — вычисление квадратного корня, F — операция a-bc, Div — деление, In — входные данные, Out — выходные.

1.7.2 Генерация вектора Y

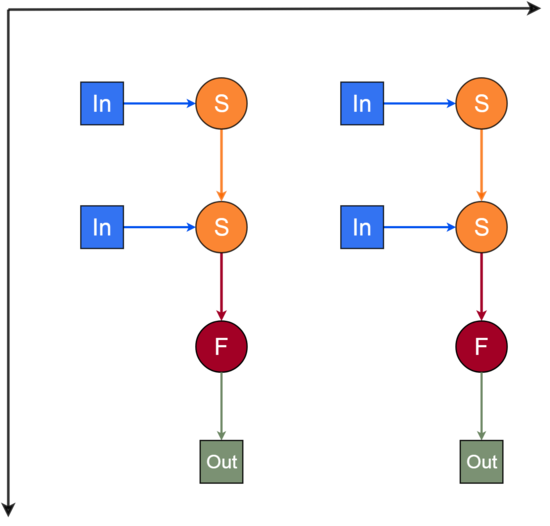
Граф этапа 2 макроструктуры алгоритма состоит из двух групп вершин, расположенных в целочисленных узлах двумерной области.

Естественно введённые координаты области таковы:

• $i$ — меняется в диапазоне от $1$ до $n$, принимая все целочисленные значения;
• $j$ — меняется в диапазоне от $1$ до $\kappa$, принимая все целочисленные значения.

Первая группа вершин. Соответствующая ей операция вычисляет функцию $S = a+b$.

Аргументы операции следующие:

• $a:$
  • при $j=1$ — константа $0$;
  • при $j\gt 1$ — результат срабатывания операции, соответствующей вершине из первой группы, с координатами $i,j-1$;
• $b$ — элемент входных данных — значение, поступающее с $PRNG$.

Результат срабатывания операции является промежуточным данным этапа.

Вторая группа вершин. Соответствующая ей операция вычисляет функцию $F = \left(a-\frac{\kappa}{2}\right)\sqrt{\frac{12}{\kappa}}$.

Аргументы операции следующие:

• $a$ — результат срабатывания операции, соответствующей вершине из первой группы, с координатами $i,\kappa$.

Результат срабатывания операции является выходным данным этапа $y_i$.

Описанный граф можно посмотреть на рис.2, выполненном для случая $n = 2, \kappa = 2$.

Рисунок 2. Граф этапа 2 макроструктуры алгоритма

1.7.3 Вычисление вектора X

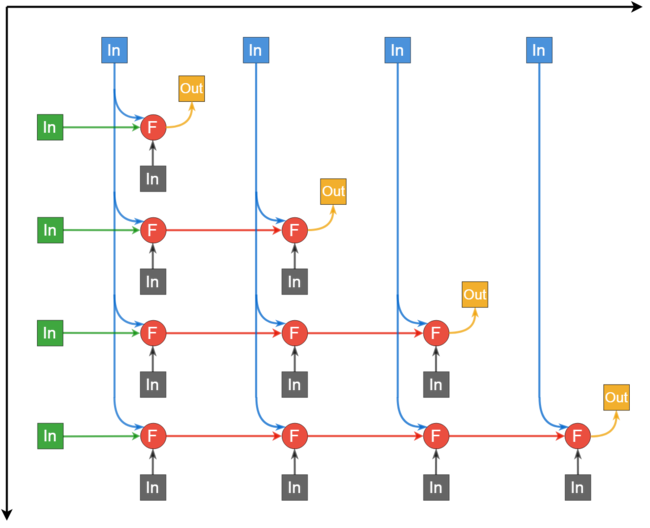
Граф этапа 3 макроструктуры алгоритма (умножение нижней треугольной матрицы на вектор и сложение результата с другим вектором) состоит из одной группы вершин, расположенной в целочисленных узлах двумерной области, соответствующая ей операция $a+bc$.

Естественно введённые координаты области таковы:

• $i$ — меняется в диапазоне от $1$ до $n$, принимая все целочисленные значения;
• $j$ — меняется в диапазоне от $1$ до $n$, принимая все целочисленные значения.

Аргументы операции следующие:

• $a$:
  • при $j = 1$ — компонента $m_{x_i}$ вектора $M$;
  • при $j \gt 1$ — результат срабатывания операции, соответствующей вершине с координатами $i, j-1$;
• $b$ — элемент входных данных $b_{ij}$;
• $c$ — элемент входных данных $y_{j}$;

Результат срабатывания операции является:

• при $j \lt i$ — промежуточным данным этапа;
• при $j = i$ — выходным данным алгоритма $x_i$.

Описанный граф можно посмотреть на рис.3, выполненном для случая $n = 4$.

Рисунок 3. Граф этапа 3 макроструктуры алгоритма, F — операция a+bc

1.8 Ресурс параллелизма алгоритма

Для разложения Холецкого $(n \times n)$ матрицы $\Sigma$ в параллельном варианте требуется последовательно выполнить следующие ярусы:

• $n$ ярусов с вычислением квадратного корня (единичные вычисления в каждом из ярусов),
• $n - 1$ ярус делений (в каждом из ярусов — линейное количество операций, в зависимости от яруса — от $1$ до $n - 1$),
• по $n - 1$ ярусов умножений и сложений/вычитаний (в каждом из ярусов — квадратичное количество операций, от $1$ до $\frac{n^2 - n}{2}$).

Для генерации $(n)$ вектора $Y$ в параллельном варианте требуется последовательно выполнить следующие ярусы:

• $\kappa$ ярусов сложений ($n$ операций в каждом из ярусов),
• $1$ ярус вычитаний, делений, умножений, вычислений квадратного корня ($n, 2n, n, n$ операций соответственно),

Для вычисления $(n)$ вектора $X$ в параллельном варианте требуется последовательно выполнить следующие ярусы:

• $n$ ярусов умножений и сложений (в каждом из ярусов — линейное количество операций, в зависимости от яруса — от $1$ до $n$)

Учитывая $n \gg \kappa$, можно заключить: при классификации по высоте ЯПФ алгоритм имеет сложность $O(n)$, при классификации по ширине — $O(n^2)$.

1.9 Входные и выходные данные алгоритма

• Входные данные: вещественная всюду плотная положительно определенная симметрическая $(n \times n)$ матрица $\Sigma$ и вещественный $(n)$ вектор $M$;
• Выходные данные: вещественный $(n)$ вектор $X$.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

// compute matrix B (core)
for (int j = 0; j < n; j++){
    double sum_down = matrix_cov[j][j];
    for (int k = 0; k < j; k++){
        double cur = matrix_cov[j][k];
        sum_down -= cur * cur;
    }
    matrix_cov[j][j] = sqrt(sum_down);
    for (int i = j + 1; i < n; i++){
        double sum_up = matrix_cov[i][j];
        for (int k = 0; k < j; k++){
            sum_up -= matrix_cov[i][k] * matrix_cov[j][k];
        }
        matrix_cov[i][j] = sum_up / matrix_cov[j][j];
    }
}
// generate vector Y
for (int i = 0; i < n; i++){
    double sum = generate_uniform(n);
    for (int j = 0; j < CLT_NUM - 1; j++){
        sum += generate_uniform(n);
    }
    vec_Y[i] = (sum - CLT_NUM / 2) * sqrt(12.0 / CLT_NUM);
}
// linear transformation
for (int i = 0; i < n; i++){  
    vec_X[i] = vec_exp[i];
    for (int k = 0; k <= i; k++){
        vec_X[i] += matrix_cov[i][k] * vec_Y[k];
    }
}

2.3 Возможные способы и особенности параллельной реализации алгоритма

В данной реализации алгоритма весь ресурс параллелизма использован в следующих этапах:

• вычисление элементов матрицы $B$ в рамках столбца (под диагональю),
• генерация вектора $Y$,
• вычисление вектора $X$ (умножение матрицы на вектор, сложение векторов).

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

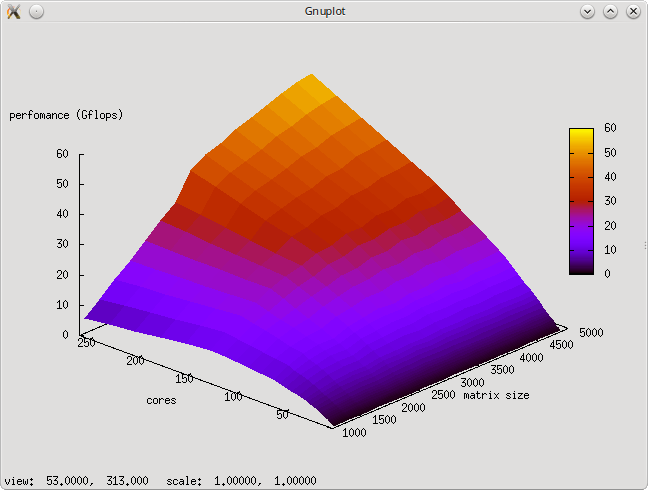
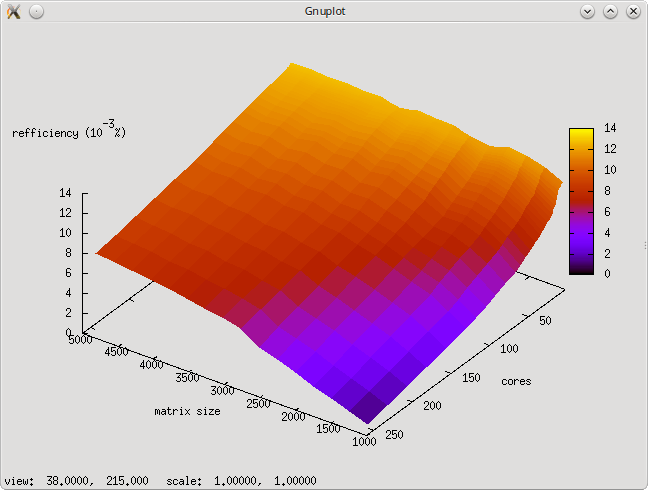
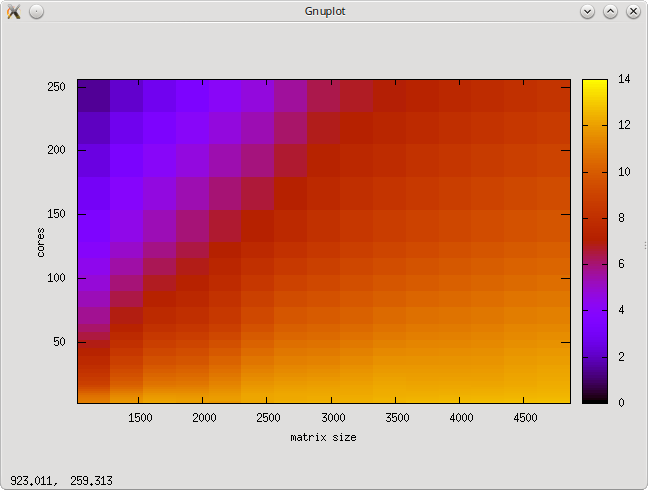
Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Алгоритм был реализован на языке C++ с использованием Intel MPI Library и запущен на кластере regular4.

Параметры компиляции и запуска:

module add slurm
module add impi/5.0.1
mpicxx -std=c++0x task.c -o _scratch/task
sbatch -n256 impi ./task <matrix_size>

Параметры запуска:

• размер матрицы [1024 : 4864] с шагом 256,
• число ядер [2 : 256] с шагом по степеням 2.

Рисунок 4. Изменение производительности в зависимости от числа ядер и размера матрицы.

Рисунок 5. Изменение эффективности реализации в зависимости от числа ядер и размера матрицы.

Рисунок 6. Изменение эффективности реализации, вид сверху.

Оценка масштабируемости:

• По размеру задачи — при увеличении размерности матрицы эффективность реализации постепенно увеличивается, при этом тем быстрее, чем большее число ядер задействовано.
• По числу ядер — при увеличении числа mpi-процессов эффективность реализации снижается. Это объясняется ростом накладных расходов на организацию параллельного выполнения. При этом с ростом размерности матрицы эффективность снижается с такой же скоростью, но уже при больших значениях числа mpi-процессов.
• По двум направлениям — эффективность реализации возрастает (на рассматриваемой области значений параметров), но крайне медленно.

Параллельная реализация на C++

2.7 Существующие реализации алгоритма

MS Excel и распространённые статистические пакеты (напр., SPSS, Statistica) позволяют моделировать только одномерные статистические распределения. Имеется возможность "собрать" многомерное распределение из нескольких одномерных при условии, что компоненты независимы. Однако если необходимо исследовать данные с зависящими друг от друга переменными, то приходится писать собственную программу. При этом удобно воспользоваться готовой реализацией разложения Холецкого (точечного метода), представленной в таких прикладных пакетах, как LINPACK, LAPACK, SCALAPACK.