Участник:Sergey Ivanov/Генетические алгоритмы

Автор текущей версии статьи: Иванов Сергей, гр. 417, 2017-ый год

1 Структура алгоритма

1.1 Описание алгоритма

Генетический алгоритм - универсальный субоптимальный метод оптимизации [math]F(x) \rightarrow \mathop{max}_x[/math]. Универсальность проявляется в его пригодности к задачам с произвольными функциями [math]F\colon \mathbb{X} \to \mathbb{R} [/math] и нетривиальной природой пространства аргументов [math]\mathbb{X}[/math].

От функции [math]F[/math] требуется только возможность вычислять её значение в произвольной точке. От пространства аргументов требуется наличие т.н. функции кроссинговера, т.е. функции [math] Crossover\colon \mathbb{X}\times \mathbb{X}\to \mathbb{X} [/math]. Обычно для этого объекты пространства представляются в виде набора генов, т.е. по сути вещественных или бинарных векторов фиксированной (или даже меняющийся по ходу оптимизации) размерности. Функция кроссинговера обычно полагается независимой для каждого гена (то есть для каждого элемента последовательности): для бинарных генов с вероятностью 1/2 берётся ген первого аргумента, иначе второго; для вещественных генов [math]g_1, g_2[/math] результатом обычно полагается [math]\alpha g_1 + (1 - \alpha) g_2[/math], где [math]\alpha \sim Unifrom(0, 1)[/math]

Такие слабые требования позволяют алгоритму работать в случаях, где традиционные методы непрерывной оптимизации неприменимы, таких как отбор признаков в задачах машинного обучения и задачи обучения с подкреплением.

Канонически использующаяся для описания алгоритма терминология взята из теории эволюции. Под "особью" в биологии понимают совокупность фенотипа и генотипа живого организма; с математической точки зрения, в рамках задачи оптимизации, можно положить, что генотипом является некоторая точка [math]x[/math], а фенотипом - значение в данной точке функции [math]F[/math]. Основная идея алгоритма заключается в том, чтобы в рамках некоторой популяции, т.е. набора особей, отобрать лучшие по фенотипу особи, а затем построить новую популяцию на основе только лучших генотипов. Одна такая итерация называется эпохой. Соответственно, два основных параметра алгоритма - размер популяции, и число отбираемых ("выживающих") особей на каждой итерации.

1.2 Математическое описание алгоритма

Входные данные: функция [math] F\colon \mathbb{X} \to \mathbb{R}[/math]

Параметры алгоритма: размер популяции [math]PopulationSize[/math], число выживающих особей на каждом этапе [math]SurvivalSize[/math], функция кроссинговера [math] Crossover\colon \mathbb{X}\times \mathbb{X}\to \mathbb{X} [/math], критерий останова. Опционально: функция мутации [math] Mutation\colon \mathbb{X}\to \mathbb{X} [/math], вероятность мутации [math]\epsilon[/math].

Выходные данные: субоптимальный экстремум [math]x*[/math]

Инициализация: [math]Population_0 := PopulationSize[/math] случайных объектов из [math]\mathbb{X}[/math]

До выполнения критерия останова:

• вычислить [math]F(x)[/math] для всех [math]x[/math] из [math]Population_i[/math]
• оставить топ-[math]SurvivalSize[/math] особей из [math]Population_i[/math]
• составить [math]Population_{i+1}[/math]: каждая новая особь есть результат применения [math]Crossover[/math] к двум случайным выжившим особям
• при наличии мутаций к каждой особи с вероятностью [math]\epsilon[/math] применить функцию [math]Mutation[/math]

На выход алгоритм подаётся [math]\mathop{argmax}_{x \in Population_{last}} F(x)[/math]

1.2.1 Возможные вариации

Стоит отдельно отметить, что алгоритм допускает бесчисленное количество вариаций, и редко применяется в исходной форме. Модификациям можно подвергнуть практически любой этап алгоритма без существенного изменения идеи процесса. Большинство модификаций призвано бороться с главным недостатком алгоритма - отсутствием вариативности, вызванной похожестью результата операции кроссинговера на свои операнды. Ниже перечислены некоторые из возможных модификаций:

• битвы на выживание: на этапе отбора выбирать две случайные особи и устраивать между ними "сражение", в котором одна из них "погибает" (удаляется из популяции). Сражение может проходить по принципу "побеждает сильнейший", или стохастически, с вероятностью победы пропорциональной силе особи, где сила - значение функции [math]F[/math].
• острова: запускать генетический поиск для нескольких независимо сэмплированных популяций и допускать редкие обмены генотипами между ними. Нестрого говоря, это позволяет найти несколько локальных максимумов, и проверить, нет ли лучших вариантов между ними.
• старение: оставлять топ-k особей популяции неизменными для следующего поколения; удалять их, если их "возраст" превысил определённый порог.

1.3 Вычислительное ядро алгоритма

В типичной ситуации вычислительным ядром алгоритма является вычисление [math]PopulationSize[/math] значений оптимизируемой функции [math]F[/math]. Основными причинами такого положения являются следующие:

• генетические алгоритмы "специализированы" для оптимизации функций, для которых вычисление значения в точке является нетривиальной или достаточно вычислительно трудоёмкой процедурой.
• все остальные макрооперации алгоритма обычно имеют сложность или линейную от размерности пространства аргументов, или [math]O(PopulationSize \log PopulationSize)[/math], где [math]PopulationSize[/math] редко превосходит 1000

1.4 Макроструктура алгоритма

Алгоритм, как видно из математического описания алгоритма, состоит в проведении следующих макроопераций:

• вычисление значений [math]F[/math] для каждой особи
• сортировка полученных значений
• сэмплирование индексов родителей для каждой особи из дискретного равномерного распределения
• проведение кроссинговера для генерации новых особей (типично представляет собой поэлементную процедуру над двумя векторами)

1.5 Схема реализации последовательного алгоритма

1. Провести инициализацию первой популяции [math]{x}[/math]

2. Для каждой особи вычислить значение [math]f_i = F(x_i)[/math]

3. Отсортировать особи по массиву значений [math]f_i[/math]

4. Проверить критерий останова. Если он выполнен, ответом алгоритма является [math]x_0[/math]

5. Для каждой особи засэмплировать [math]p_{i1}, p_{i2} \sim \mathcal{U}\{0, SelectionSize\}[/math]

6. Составить [math]{y_i = Crossover(x_{p_{i1}}, x_{p_{i2}})}[/math]

7. Положить [math]{x} = {y}[/math]

8. Перейти к пункту 2

1.6 Последовательная сложность алгоритма

Предположим, что сложность одного вычисления фитнес-функции имеет сложность [math]F[/math], процедура кроссинговера --- [math]D[/math]; размер популяции для сокращения выкладок обозначим [math]P[/math]. Рассчитаем сложность одной эпохи алгоритма:

Этап 2 является наиболее вычислительно трудоёмким и имеет сложность [math]PF[/math];

Этап 3 имеет сложность [math]P \log P [/math].

Этапы 4-5 имеют константную сложность.

Этап 6 имеет сложность [math]PD[/math].

Этап 7 также имеет сложность [math]PD[/math].

Для произвольной [math]F[/math] в общем случае сложность алгоритма составляет [math]O(PF + P \log P + PD)[/math], обычно выбор параметров таков, что вторым слагаемым можно пренебречь. Зачастую соотношение между [math]F[/math] и [math]D[/math] таково, что сложность по факту становится [math]O(PF)[/math].

При этом в памяти необходимо хранить два массива из [math]P[/math] объектов из пространства [math]\mathbb{X}[/math]. В предположении, что его размерность совпадает со сложностью кроссинговера, это [math]2PD[/math] вещественных чисел.

1.7 Информационный граф

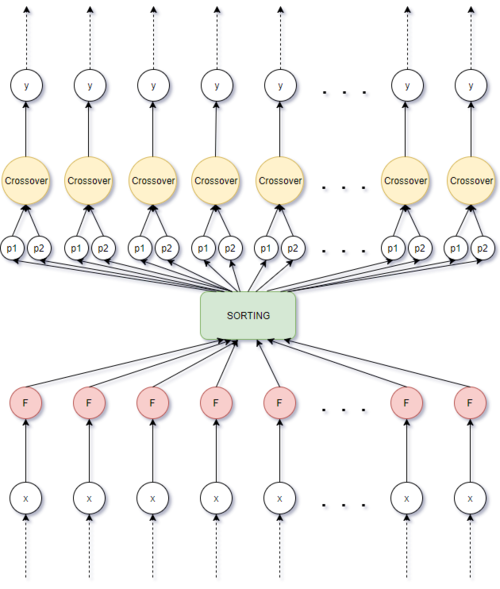
На рис.1 показана информационная структура типичного генетического поиска. Стоит отметить, что на рисунке p1 и p2 формально являются не индексами родителей, а их генотипами, т.е. с точки зрения данного графа процедура сортировки возвращает отсортированный список именно что объектов [math]{x}[/math]; более частой реализацией является применение кроссинговера к особям с сэмплированными индексами, в таком случае формально требовалось бы соединить каждую из операций кроссинговера со всеми [math]x[/math], получая таким образом на графе полносвязную структуру, являющуюся основным препятствием к распараллеливанию алгоритма.

Рис.1. Информационный граф генетического поиска

Формально граф на рис.1 состоит из следующих элементов:

• для очередной популяции высчитываются значения фитнес-функции. Это происходит независимо для каждой особи, и может быть сделано параллельно.
• полученный набор значений подаётся на вход алгоритму сортировки [math]{x}[/math] в качестве критерия сортировки.
• вычисляются генотипы p1, p2 среди случайных особей, оказавшихся в топ-[math]SelectionSize[/math] по результатам сортировки
• после предыдущей операции к генотипам p1, p2 независимо для каждой особи применяется [math]Crossover[/math]
• полученные значения становятся новыми особями популяции

1.8 Ресурс параллелизма алгоритма

На информационном графе на рис. 1 видно, что все вычисления фитнес-функции, самой трудоёмкой операции алгоритма, на одной эпохе можно распараллелить. Это позволяет в общем случае снизить стоимость одной эпохи с [math]O(PN)[/math] до [math]O(N)[/math], и при больших [math]N[/math] эта сложность принципиально неулучшаема (на каждом шаге оптимизации функции, для которой мы умеем только считать значение в некоторой точке, не может быть ничего оптимальнее, чем сделать это один раз). При возможности неограниченно распараллеливать вычисление, одна эпоха генетического алгоритма начинает стоить всего один вызов функции [math]F[/math], что фундаментально является существенным преимуществом алгоритма.

Информационный граф показывает, что также доступна для распараллеливания и операция кроссинговера. Однако, для этого требуется каждому процессу получить доступ к двум требуемым генотипам, находящимся у двух других процессов. В возникающей схеме взаимных обменов информации потенциальные затраты на организацию доступа и передачу данных могут оказаться выше проведения кроссинговера [math]P[/math] раз на одном процессоре, однако такая альтернатива существует, и, особенно при нелинейной сложности кроссинговера, её стоит принимать во внимание.

Поскольку алгоритм эвристический, в оптимизационных целях был придуман ряд эвристик, направленных на увеличение потенциала распараллеливания:

• индексы родителей могут сэмплироваться так, чтобы заранее упростить процесс обмена сообщениями; в предельной идее, например, индексы родителей из топа-[math]SelectionSize[/math] для каждой новой особи можно зафиксировать, чтобы точно указать на информационном графе, какие именно генотипы для какой операции кроссинговера используются.
• отчасти упрощает распараллеливание такое ответвление генетического поиска, как естественный генетический поиск, в целом являющимся Монте-Карло методом оценки невычислимого градиента.

1.9 Входные и выходные данные алгоритма

Входные данные: функция [math]f: \mathbb{X} \to \mathbb{R} [/math]; [math]\mathbb{X}[/math] должно иметь некоторое программное представление, например, определена некоторая инъекция [math]\mathbb{R}^d \to \mathbb{X}[/math].

Выходные данные: субоптимальный [math]x \in \mathbb{X}[/math]

Параметры:

• размер популяции (100-1000)
• количество особей для отбора (например, относительно объёма размера популяции; обычно 5-50%)
• операция кроссинговера [math] Crossover\colon \mathbb{X}\times \mathbb{X}\to \mathbb{X} [/math]. Обычно это одна из типично используемых процедур: поэлементное среднее, какая-либо её стохастическая модификация, случайный выбор для каждого гена, от какого родителя взять значение.
• вероятность мутации одного гена; обычно 0,01 или меньше.
• критерий останова: например, достижение определённого результата или ограничение на количество эпох.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

На суперкомпьютере "Ломоносов" была проведена экспериментальная оценка сильной масштабируемости для задачи квадратичной сложности от размерности данных (100) с объёмом популяции 1000 и количеством отбираемых особей 100. В качестве операции кроссинговера было взято поэлементное среднее, один ген мутировал (сэмплировался случайно из диапазона [math][0, 1][/math]) с вероятностью 0.01. Для количества процессоров 1, 2 ... 128 было проведено по три замера времени; для 256 и 512 два замера. Результаты приведены на рис.2

Рис.2. Сильная масштабируемость генетической оптимизации

Узким горлом алгоритма для распараллеливания является процедура сортировки и последующего сэмплирования индексов родителей на основе результатов этого процесса, а точнее, сопряжённая с этим передача данных. В версии, для которой был проведён эксперимент, один процесс отвечал за сортировку и последующий кроссинговер, после чего передавал генотипы другим процессам для вычисления значения функции в этих точках. Видно, что начиная с некоторого количества процессоров, где-то 64-128, затраты на передачу массивов длины [math]D=100[/math] от одного процесса остальным начали перекрывать выигрыш от увеличения числа процессоров. Поэтому потенциально такая реализация не является оптимальной.