DevbunovaViliana / Метод главных компонент (PСA)

Автор: Девбунова Вилиана Олеговна, студент ММП ВМК МГУ (417)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Главных Компонент (англ. Principal Components Analysis, PCA) — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Изобретен К. Пирсоном (англ.Karl Pearson) в 1901 г. Применяется во многих областях, таких как распознавание образов, компьютерное зрение, сжатие данных и т. п. Вычисление главных компонент сводится к вычислению собственных векторов и собственных значений ковариационной матрицы исходных данных или к сингулярному разложению матрицы данных.

Иногда метод главных компонент называют преобразованием Кархунена-Лоэва (англ. Karhunen-Loeve)или преобразованием Хотеллинга (англ. Hotelling transform). Другие способы уменьшения размерности данных — это метод независимых компонент, многомерное шкалирование, а также многочисленные нелинейные обобщения: метод главных кривых и многообразий, поиск наилучшей проекции (англ. Projection Pursuit), нейросетевые методы «узкого горла», самоорганизующиеся карты Кохонена и др.

1.2 Математическое описание алгоритма

Задача анализа главных компонент имеет много версий, вот базовые из них:

• аппроксимировать данные линейными многообразиями меньшей размерности;
• найти подпространства меньшей размерности, в ортогональной проекции на которые разброс данных максимален;
• найти подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально;
• для данной многомерной случайной величины построить такое ортогональное преобразование координат, в результате которого корреляции между отдельными координатами обратятся в нуль.

Мы будем рассматривать только один вариант.

1.3 Вычислительное ядро алгоритма

Мы будем реализовывать PCA с помощью нахождения подпространства меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально. Для вычисления собственных значений и соответствующих им собственных векторов будем использовать метод степенных итераций

1.3.1 Алгоритм вычисления собственных значений метод степенных итераций

Метод степенных итераций - это итерационный метод вычисления собственных значений и собственных векторов вещественной матрицы. Алгоритм вычисляет вектор $e$, содержащий собственные значения , и матрицу $E$, содержащую соответствующие собственные векторы, т. е. $e_i$-собственное значение, а столбец $E_i$-ортонормированный собственный вектор для $e_i$, для $i = 1,...,n$.

1.3.2 Задача нахождения подпространства меньшей размерности

Будем искать подпространство меньшей размерности, в ортогональной проекции на которые среднеквадратичное расстояние между точками максимально. Будем использовать жадную стратегию: Будем подбирать единичные вектора $E_i$, такие что норма проекций на этот вектор будет максимальна.

• 1.$||M E_1||^2 → max_{E_1}$
• 2. $|M E_2||^2 → max_{E_2}$ и $E_1$ ортогонален $E_2$
• 3. и т.д.

Запишем задачу Лагранжа: $\frac{d}{dE_1}(E_1^TM^TME_1 - \lambda(E_1^TE_1 -1) = 0$

$M^TME_1 - \lambda E_1 = 0$ Значит, задача сводится к последовательному нахождению собственных векторов, отвечающих максимальным собственным значениям матрицы $M^TM$

Алгоритм:

• 1. Вычислить эрмитов матрицу (найти сопряженную транспонированную), $M^T$ из матрицы $M$.
• 2. Вычислить умножение $M^TM$
• 3. Вычислить собственные значения и собственные векторы $M^TM$, используя аметод степенных итераций.
• 4. Отсортировать собственные значения и соответствующие столбцы собственных векторов в порядке убывания собственных значений. И взять первые $k$ собственных векторов, отвечающих максимальным собственным значениям.

1.3.3 Анализ основных компонентов (PCA)

Анализ главных компонент, или сокращенно PCA, - это математическая процедура, которая преобразует набор (возможно коррелированных) переменных в меньшее число некоррелированных переменных, которые называют главными компонентами. Цель анализа главных компонент состоит в том, чтобы уменьшить размерность (количество признаков) набора данных, но сохранить как можно больше исходной изменчивости в данных. На первый основной компонент приходится большая часть изменчивости данных, на второй основной компонент приходится большая часть оставшейся изменчивости и т. д. PCA можно рассматривать как метод проекции, при котором данные с $n$-признаками проецируются на подпространство с $n$ (или меньшим количеством) признаков, сохраняя при этом большую часть информации. Мы будем внешне задавать размерность признанного пространства, которое хотим получить $k$.

1.4 Макроструктура алгоритма

Макроструктура алгоритма:

• 1. Вычислить $M^T$ из матрицы $M$.
• 2. Вычислить умножение $M^TM$
• 3. В цикле до сходимости вычислять:

$E_{k+1} = \frac{M^TME_k}{\|M^TME_k\|}$ -- сойдется к собственному вектору, отвечающему максимальному значению, тогда последовательность $\lambda_{k+1} = \frac{(E_k,M^TME_k)}{(E_k,E_k)}$ сойдется к максимальному собственному значению.

• 4. Теперь вместо выражения $M^TM$ в пункте 3 используем

$M^TM - \lambda_k E_k E_k^T$

• 5. Повторяем пункт 3 и 4 столько раз, какой размерности хотим получить новое пространство.

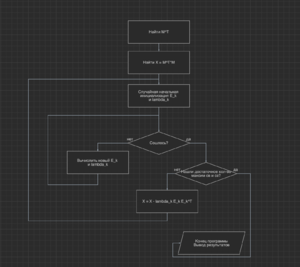
1.5 Схема реализации последовательного алгоритма

Блок-схема алгоритма

1.6 Последовательная сложность алгоритма

Оценим сложности операций. Пусть $n$ -- количество объектов в выборке, $d$ -- размерность пространства признаков, $k$ -- размерность итогового пространства (но так как основной смысл задачи -- это понижение размерности, то $k \lt \lt n$ и $k \lt \lt d$, поэтому мы не будем учитывать его при подсчете асимптотической сложности), тогда: нахождение транспонированной матрицы $O(n*d)$, перемножение $M^TM$имеет сложность $O(n*d^2)$, случайная генерация вектора $O(d)$, вычисление $E_k$ состоит из перемножения матрицы на вектор, что занимает $O(d^2)$, вычисление нормы вектора $O(d)$ и покомпонентного деление вектора на константу $O(d)$. Подсчет $\lambda_k$ использует уже посчитанное для $E_k$ умножение матрицы на вектор, дополнительно происходит два раза скалярное произведение над векторами $O(d)$, и поэлементное деление вектора на константу $O(d)$. Вычисление $\lambda_k E_k E_k^T$ занимает $O(d^2)$, вычитание матриц имеет сложность $O(d^2)$.

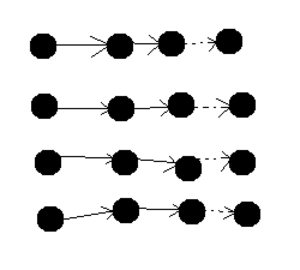
1.7 Информационный граф

Так как алгоритм очень объемный и его не возможно представить в 3-ех мерном пространстве, то изобразим информационный граф самой частой операции в алгоритме: умножение матрицы на вектор.

Информационный граф умножения матрицы на вектор

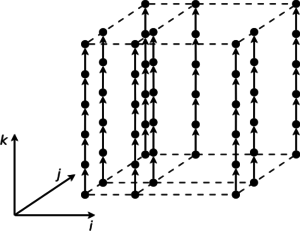
Одной из самых сложных операций в алгоритме является операция перемножения матриц, ее информационный граф выглядит следующим образом:

Информационный граф перемножения матриц

1.8 Ресурс параллелизма алгоритма

Если посмотреть на блок-схему алгоритма, то видно, что он строго последовательный на макроуровне, но отдельно взятые операции можно распараллелить. Причем они могут быть распараллелены покоординатно (так как имеют независимость итераций в некоторых циклах): умножение матриц, деление вектора на константу, умножение вектора на константу, транспонирование матрицы, вычитание матриц, умножение матрицы на число. К примеру, для умножения квадратной матрицы $R^{d×d}$ на вектор $R^d$ нужно последовательно выполнить по $d$ ярусов умножений и сложений, где в каждом ярусе $d$ операций. Для алгоритма умножения матриц $R^{d×n}$ на $R^{n×d}$ требуется последовательно выполнить по $n$ ярусов умножений и сложений, где в каждом из ярусов $d^2$ операций.

1.9 Входные и выходные данные алгоритма

На вход алгоритма поступает матрица $M \in R^{n×d}$, где по строкам записано признаковое представление объектов и число k до какого размера мы хотим сократить размерность пространства признаков (обычно $k \lt \lt d$). На выходе мы получаем $k$ векторов и соответствующих им собственных значений матрицы $M^TM$, отсортированных в порядке убывания. Проекция объектов из $M$ на эти вектора дает новое представление этих объектов, но в пространстве размерности $k$, и это есть наилучшее представление для данной размерности (потеряли наименьшее количество информации при переходе).

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Время работы PCA относительно количества потоков и размерности пространства признаков

К сожалению, мы не можем рассчитать в GFlops, потому что не можем точно сказать количество операций (не знаем за сколько шагов у нас сойдется собственное значение и собственный векторв).

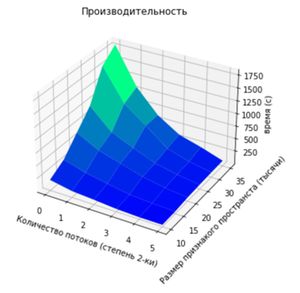
Проведем оценку масштабируемости:

• 1. По количеству потоков: При увеличении количества потоков время работы алгоритма уменьшается. Отметим, что с каждым увеличением количества потоков уменьшается скорость роста времени работы при фиксированном колличестве потоков и увеличении размера признакого пространства.
• 2. По размеру пространства признаков: С увеличением размера данных задача считается дольше. Аналогично, заметим, что если брать график времени работы относительно фиксированного размера признаков: берем график времени в зависимости от количества потоков при 10 тысячах признаков, потом при 15, 20 и так далее, увидим, что скорость падения нашей функции с ростом размерности пространства увеличивается.
• 3. По двум напрвлениям сразу: Время работы алгоритма монотонно уменьшается с увеличением количества потоков и уменьшением размера признакого пространства одновременно.

2.7 Существующие реализации алгоритма

Есть реализация метода главных компонент в библиотеке scikit-learn для Python. Ссылка на библиотечный метод. Но сам код реализации посмотреть невозможно, потому что это библиотека с закрытым кодом.

3 Литература

[1] Wikipedia contributors. Principal component analysis. In Wikipedia, The Free Encyclopedia from https://en.wikipedia.org/wiki/Principal_component_analysis