Newton's method for systems of nonlinear equations, scalability2

Основные авторы описания: А.Чернышев, Н.Захаров.

1 Ссылки

В качестве модельной задачи рассматривался один из примеров, поставляемых вместе с модулем SNES пакета PETSc.

3 Масштабируемость алгоритма и его реализации

Масштабируемость алгоритма и его реализаций определяется главным образом масштабируемостью реализации алгоритма решения СЛАУ, используемого для нахождения изменения текущего решения на очередной итерации.

3.2 Масштабируемость реализации алгоритма

Тестирование алгоритма проводилось на суперкомпьютере "Ломоносов"Суперкомпьютерного комплекса Московского университета.

• Версия MPI - impi/4.1.0
• Реализация BLAS - mkl/11.2.0
• Запуски проводились в сегменте regulal4
• Модель используемого CPU - Intel Xeon X5570 2.93GHz
• Версия PETSc - 3.7.4
• Флаги компиляции: -fPIC -Wall -Wwrite-strings -Wno-strict-aliasing -Wno-unknown-pragmas -fvisibility=hidden -g3

Кроме того, использовались следующие параметры:

1. Pестарт алгоритма GMRES через 300 итераций
2. Максимальное число итераций для нахождения решения СЛАУ - 1500
3. Максимальное число итераций метода Ньютона на данном этапе решения - 20

Набор начальных параметров:

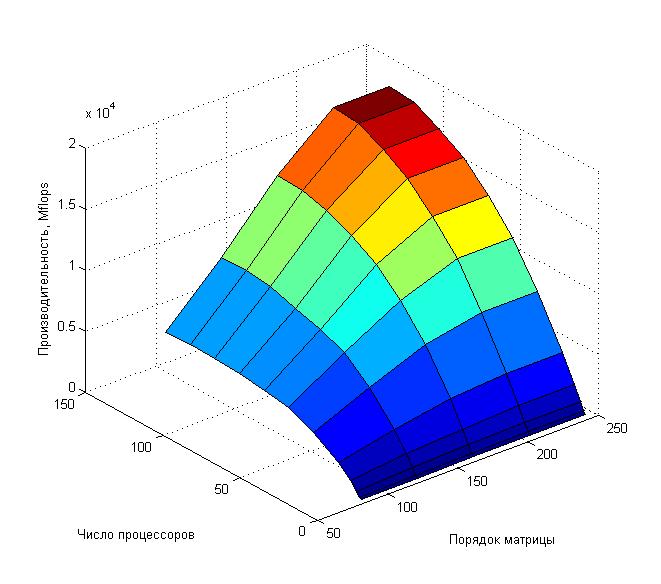
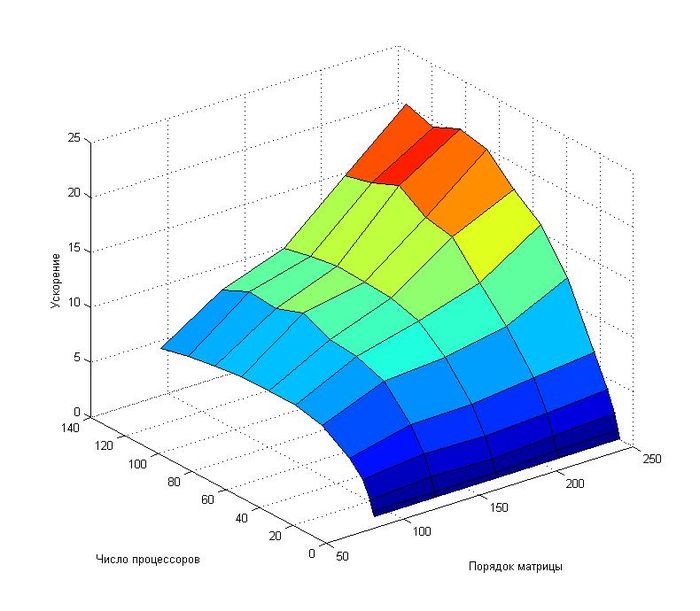
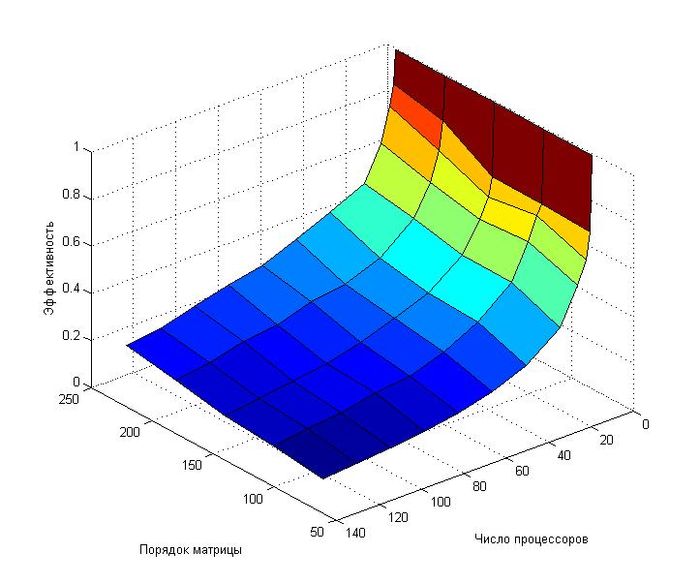
• Число процессоров [1 2 4 8 16 32 48 64 80 96 112 128];
• Порядок матрицы [82 122 162 202 242].

Рис. 1. Изменение производительности в зависимости от числа процессоров и размера матрицы.

Рис. 2. Изменение ускорения в зависимости от числа процессоров и размера матрицы.

Рис. 3. Изменение эффективности в зависимости от числа процессоров и размера матрицы

Как видно из приведенных графиков, эффективность распараллеливания алгоритма довольно быстро убывает при увеличении числа процессоров.

При фиксированном числе процессоров наблюдается рост ускорения при увеличении вычислительной сложности задачи.