Numerical quadrature (cubature) rules on an interval (for a multidimensional cube), scalability

Основные авторы описания: А.В.Смирнов, А.Б.Кукаркин.

1 Ссылки

Реализация алгоритма доступна по адресу [1].

2 Локальность данных и вычислений

Локальность операций существенно определяется реализацией вычисления функции [math]f[/math]. Если рассматривать ее вычисление как «черный ящик», то забота об эффективном использовании подсистемы памяти полностью перекладывается на его готовую реализацию.

3 Масштабируемость алгоритма и его реализации

3.2 Масштабируемость реализации алгоритма

Теоретические оценки показывают, что алгоритм должен быть превосходно масштабируем. Для демонстрации этого утверждения на конкретном примере, в НИВЦ МГУ была создана реализация алгоритма интегрирования методом прямоугольников. В качестве тестового примера рассматривалось трехмерное интегрирование. Поскольку в задачи не входила оценка сложности вычисления той или иной функции от трех переменных, было выбрано простейшее подынтегральное выражение [math]x_1^2+x_2^2+x_3^3[/math]. Однако такая функция является слишком простой и нетипичной для тех примеров, на которых обычно применяется алгоритм. Поэтому для демонстрации масштабируемости алгоритма на достаточно сложных примерах при вычислении функции в одной точке была заложена пауза длительностью в 0.01 секунды (для типичных примеров длительность может существенно превышать это время, однако и оно оказалось достаточным для проведения демонстрации масштабируемости).

В качестве метода распараллеливания данный алгоритм использует технологию MPI. Тесты проводились на суперкомпьютере Ломоносов. Для демонстрации оказалось достаточным провести тесты с количеством процессоров до 64 (с шагом 8). Для количества точек, в которых вычислялась функция, была введена логарифмическая шкала (от 100 до миллиона с шагом умножения на 10). Причина введения такой шкалы состоит в том, что в настоящих примерах требуется вычислять функцию не меньше, чем в ста тысячах точек и эта величина может доходить до одного миллиарда, а провал эффективности наблюдается лишь при существенно меньших количествах точек интегрирования. При таком подходе не представлялось возможным измерять производительность в гигафлопсах; в качестве показателя производительности использовалось количество точек, в которых была вычислена функция.

В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 27.20%;
• максимальная эффективность реализации 98.01%.

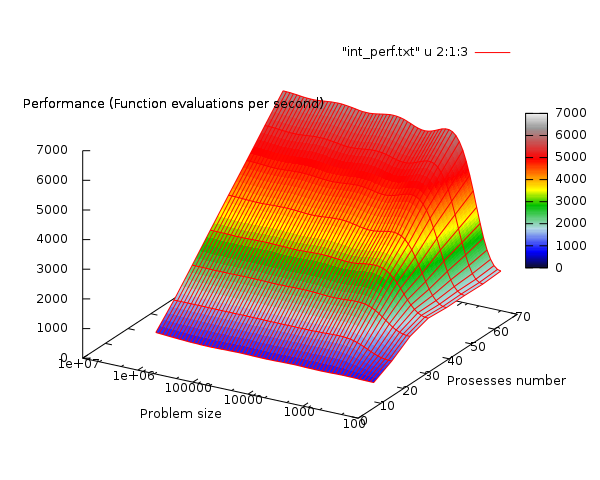
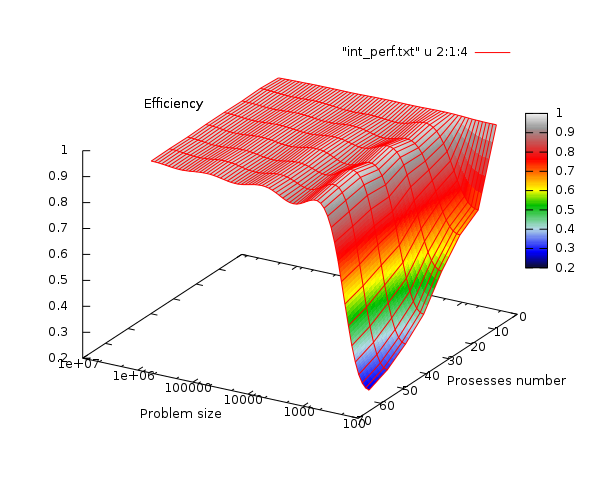
На следующих рисунках приведены графики производительности и эффективности выбранной реализации численного интегрирования в зависимости от изменяемых параметров запуска.

Рисунок 1. Параллельная реализация интегрирования методом прямоугольников. Изменение производительности в зависимости от числа процессоров и количества вычисляемых точек.

Рисунок 2. Параллельная реализация интегрирования методом прямоугольников. Изменение эффективности в зависимости от числа процессоров и количества вычисляемых точек.

При полученных данных не представляется осмысленным выводить средние оценки изменения эффективности по тем или иным осям. Эффективность вычислений для задачи существенно зависит от того, превышает ли количество вычисляемых точек количество процессоров (хотя бы на порядок). В таком случае получаемое ускорение практически линейно, а эффективность реализации стремится к единице. Поскольку в реальных примерах сложно представить, чтобы в этом алгоритме количество используемых процессоров могло сравняться с количеством вычисляемых точек, делается вывод, что алгоритм, как и предполагалось согласно теоретическим оценкам, является идеально масштабируемым.

4 Динамические характеристики и эффективность реализации алгоритма

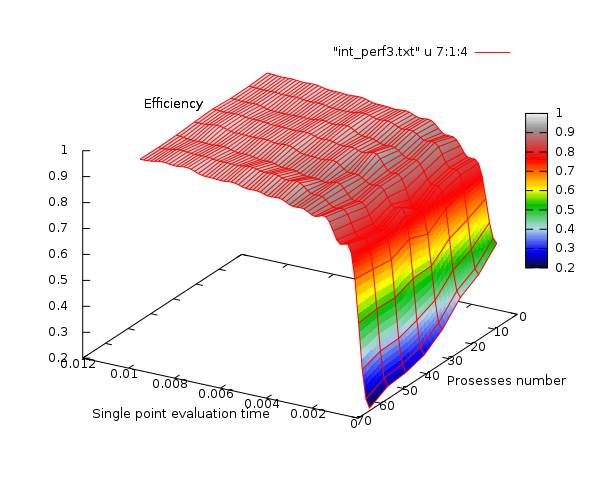
Так как мы рассматриваем вычисление функции как абстрактно устроенную и неизвестную нам процедуру, то представляется невозможным прокомментировать эффективность работы алгоритма с памятью или иные близкие характеристики. Как показали результаты предыдущего параграфа, алгоритм проявляет себя крайне эффективно в случае, когда количество вычисляемых точек становится существенно больше числа задействованных процессоров, а время вычисления функции не меньше одной сотой секунды. Соответственно представляет интерес зафиксировать количество вычисляемых точек (например, числом 10000) и изучить зависимость эффективности от числа процессоров (как и ранее, до 64 с шагом 8) и времени вычисления функции в одной точке (от [math]10^{-5}[/math] секунды до [math]101 \cdot 10^{-5}[/math] с шагом [math]10^{-4}[/math]).

Рисунок 3. Параллельная реализация интегрирования методом прямоугольников. Изменение эффективности в зависимости от числа процессоров и времени вычисления функции.

Данный эксперимент показывает, что действительно при малом времени вычисления функции в одной точке эффективность алгоритма резко падает (до 2.02% в некоторых случаях). Это объясняется тем, что накладные расходы на организацию MPI-вычислений начинают доминировать. Однако при времени вычисления функции превышающим [math]3 \cdot 10^{-4}[/math] эффективность резко возрастает и становится близкой к единице.

Суммируя результаты экспериментов можно сделать вывод, что у алгоритма есть некоторая граница, зависящая от времени вычисления функции, ниже которой параллельная реализация имеет крайне низкую эффективность (точное значение данной границы может зависеть от архитектуры кластера, но не должно превышать сотую долю секунды). Однако, после перехода этой границы эффективность быстро возрастает и приближается к единице, при этом от числа процессоров она также зависит несущественно. Число процессоров для эффективной работы, в свою очередь, должно быть меньше хотя бы на порядок, чем число точек, в которых происходит вычисление функции.